Математическая модель воздействий на радиоэлектронные средства (РЭС)

Случайные воздействия формируются с использованием генераторов независимых случайных чисел с различными законами распределения, имеющихся практически во всех ППП. При необходимости сформировать случайные числа с законами распределения, отсутствующими в ППП, можно воспользоваться методом нелинейного преобразования или методом отбора. В обоих методах используются датчики случайных чисел с равномерным законом распределения в интервале [0,1).
Требование безошибочного моделирования другое! Отсчеты выходного сигнала РЭС через интервал дискретизации Тд в моделируемой непрерывной системе y(t=nTд) и в ее цифровой модели y[nTд] должны быть равными. Требования, при которых эти условия выполняются пока не сформулированы. Но, учитывая, что обработка сигнала в ЦВМ происходит, как правило, при его линейной аппроксимации, следует потребовать, чтобы отличие непрерывного сигнала от его кусочно-линейной аппроксимации было незначительным. Поэтому при моделировании интервал дискретизации берется примерно на порядок меньше, чем по Котельникову.
Наиболее известным методом нелинейного преобразования является метод обратной функции распределения

Метод обратной функции распределения
Предположим, что случайная величина X формируется из равномерно распределенной случайной величины U функцией x=f(u).
Из функциональной связи случайных величин следует, что вероятности того, что случайная величина U меньше значения u, а случайная величина X меньше значения x, одинаковы. Другими словами, их функции распределения равны:
Fu(u) = Fx(x).
Недостаток метода: обратную функцию распределения в аналитической форме можно найти лишь для ограниченного вида распределений.

Метод отбора
Требуется сгенерировать случайную величину X с законом распределения, заданным плотностью вероятности f(x) в интервале (xмин, xмакс). Она получается отбором из равномерно распределенных случайных чисел U тех значений, которые соответствуют требуемому закону распределения.
Для отбора генерируется еще одна случайная величина V, равномерно распределенная в интервале [0, f(x)макс). Если точка отображающая пару значений (u, v) лежит ниже f(x), то значение u отбирается и принимается за значение x. Если выше f(x), то отвергается. Так, значение u1 будет приниматься всегда, а значение u2 в среднем наполовину.

1. Стандартным датчиком генерируется случайное число W, равномерно распределенное в интервале [0,1).
2. Линейным преобразованием u=xмин – (xмакс – xмин)w образуется значение случайного числа U.
3. Стандартным датчиком генерируется случайное число W, равномерно распределенное в интервале [0,1).
4. Линейным преобразованием v=f(x)максw образуется значение случайного числа V.
5. Если v меньше f(u), то u отбирается; если v больше f(u), то u отвергается.
Алгоритм отбора следующий.
Отбор продолжается, пока не сформируется массив X нужной длины.

Экспериментальная оценка закона распределения
Оценка закона распределения производится по гистограмме распределения. Проводится N испытаний, в результате которых получаются N значений случайной величины X, расположенных между минимальным xмин и максимальным xмакс значениями. Весь диапазон значений (xмакс – xмин) делится на k интервалов, которые называют разрядами, и подсчитывается число значений случайной величины ni, попадающих в i-ый разряд. Тогда частота попадания в i-ый разряд pi = ni/N. Длина разряда ∆x = (xмакс – xмин)/k. Гистограмма распределения – это столбиковая диаграмма, показывающая частоту попадания случайной величины в заданный разряд.
0,2
0,4
x

По гистограмме распределения можно оценить плотность вероятности и функцию распределения. Перерисуем гистограмму, отложив по вертикальной оси отношение pi/∆x. Длительность разряда ∆x = 0,2.

Компьютерная модель РЭС
Компьютерная модель РЭС - это программный продукт, позволяющий провести исследование РЭС проведением вычислительного эксперимента. Компьютерная модель состоит из 1) прикладной программы РЭС, составленной на основе математической модели, и 2) обслуживающих программ, обеспечивающих выполнение прикладной программы и представление результатов моделирования в удобной для пользователя форме.
Компьютерные модели делят на два вида: аналитические и имитационные. Аналитическая модель описывается математическим выражением, позволяющим сразу найти искомые переменные. Имитационная модель описывается совокупностью математических выражений, выполняющихся последовательно в том же порядке, в каком происходит обработка процессов в моделируемой системе.
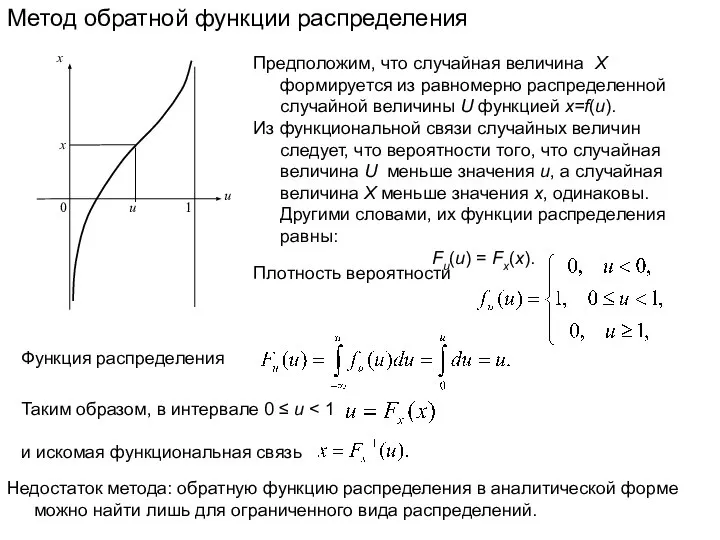
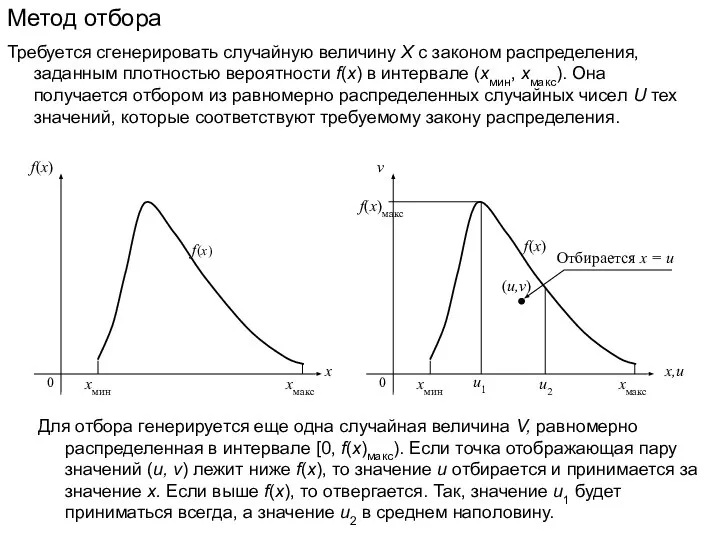
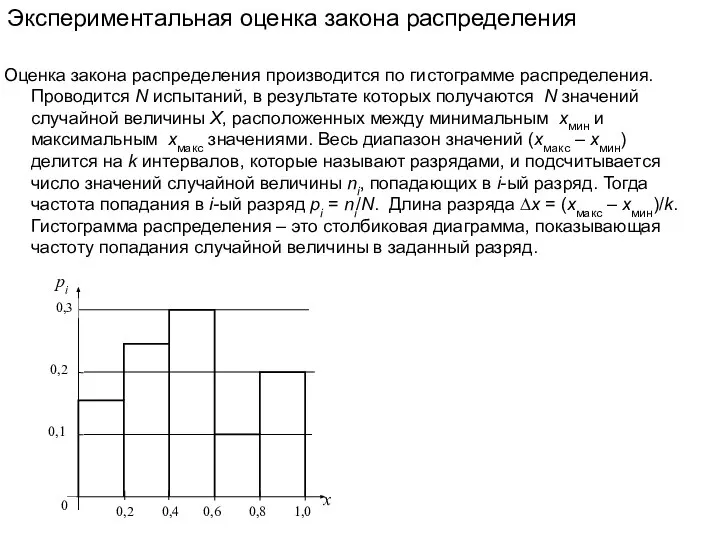
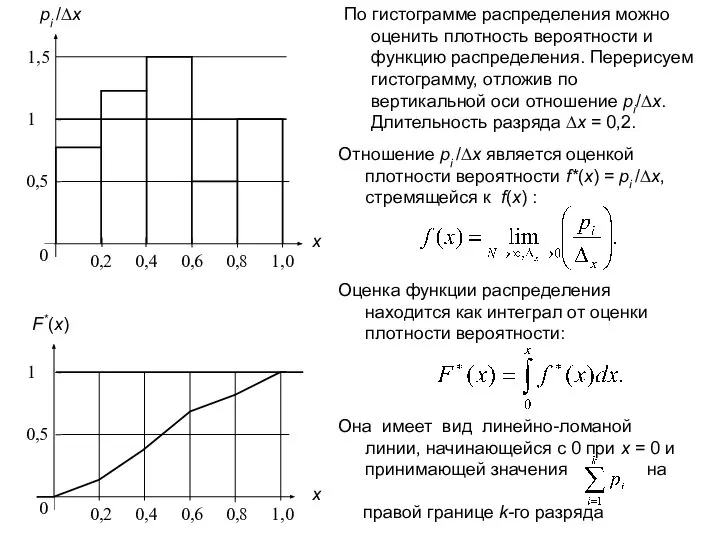
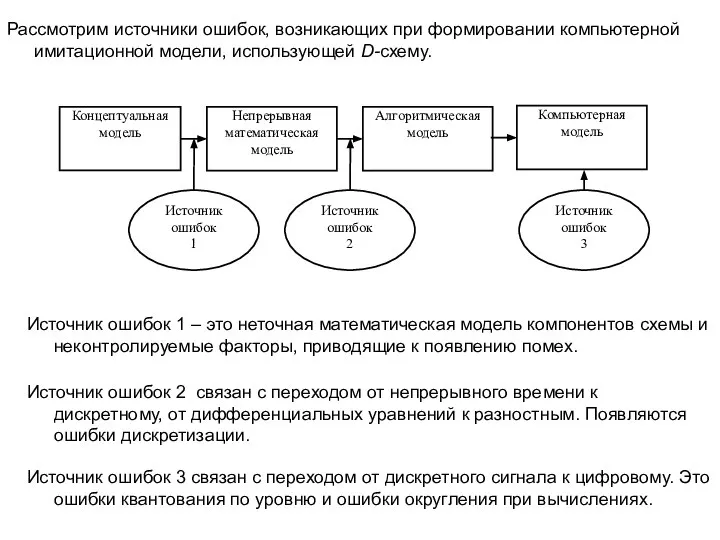
Один из главных вопросов вычислительного эксперимента, проводимого на имитационной модели, – насколько его результаты адекватны результатам натурного эксперимента, другими словами, насколько результаты моделирования близки к результатам макетирования. Для компьютерной модели этот вопрос можно сформулировать так: насколько точно модель описывает систему.

Рассмотрим источники ошибок, возникающих при формировании компьютерной имитационной модели, использующей D-схему.
Источник ошибок 1 – это неточная математическая модель компонентов схемы и неконтролируемые факторы, приводящие к появлению помех.
Источник ошибок 2 связан с переходом от непрерывного времени к дискретному, от дифференциальных уравнений к разностным. Появляются ошибки дискретизации.
Источник ошибок 3 связан с переходом от дискретного сигнала к цифровому. Это ошибки квантования по уровню и ошибки округления при вычислениях.