Слайд 2Музыкальная акустика
Музыкальная акустика – наука об образовании, распространении и восприятии звуков

музыки, изучает природу музыкальных звуков и созвучий, а также музыкальные системы и строи.
Слайд 3Пять основных периодов наиболее важных открытий в области музыкальной акустики.
Шестой век до

н.э.
Шестнадцатый век н.э.
Семнадцатый век
Восемнадцатый век
Конец восемнадцатого – девятнадцатый века
Слайд 4Шестой век до н.э.
Самое важное открытие – открытие связи высоты тона

и длины звучащего тела.
Наиболее яркая фамилия Пифагора –
создание монохорда (ок.500г. до н.э.).
Марк Фабий Квинталиан (30 – 96 гг. до н.э.) доказал наличие резонанса струны с помощью соломинки.
Сивериус Бетиус (480 – 525 гг. до н.э.) в пяти книгах изложил все музыкально-теоретические учения того времени.
Слайд 5Шестнадцатый век
В центре внимания исследователей стоит проблема установления связи между высотой

тона и числом колебаний тела.
Джованни Бенедетта в 1585г. Опубликовал трактат о музыкальных интервалах.
Исаак Бикман в 1618г. публикует к нему свои расчёты.
Галилео Галилей (1564 – 1642) в «Беседах и математических доказательствах» рассуждает о вибрации тел.
Слайд 6Семнадцатый век
С этого времени развивается теоретическая, математическая база музыкальной акустики.
Закон Роберта

Гука «Ut tension sic vis» является основанием для учения о звуке и для теории упругости.
Исаак Ньютон (1642 – 1727) сделал попытку создать математическую теорию волнового движения.
Слайд 7Мерсенн в 1636г. экспериментальным путём получил основные законы колебания струн.
Жозеф Савер (1653

– 1716) в своих трудах рассматривает различные источники звука музыкальных инструментов.
Брук Тейлор (1685 – 1731), автор теоремы о бесконечных рядах, рассчитал частоту основного тона струны в зависимости от её длины, веса, натяжения и ускорения силы тяжести.
Слайд 8Восемнадцатый век
Жан Д’Амблер (1717 – 1783), Леонардо Эйлер (1707 – 1783), Даниил

Бернулли (170 – 1782) и Лагранж теоретически решили проблему колеблющейся струны и получили дифференциальное уравнение её движения.
Эрнест Хланди (1756 – 1827) первым исследовал колебания вилочного камертона, установил законы колебаний стержней при различных способах возбуждения.
Слайд 9Конец восемнадцатого – девятнадцатый века.
Это время отмечено многочисленными попытками теоретического анализа волн

звука.
Жан Фурье (1768 – 1827)обосновал теорему, утверждавшую, что любую форму колеблющейся струны можно представить бесконечной суммой синусоид.
С.Д.Пауссон (1781 – 1840) рассмотрел теорию гибкой мембраны.
Слайд 10
Феликс Савер (1791-1841) занимался экспериментальными исследованиями продольных волн в пластинах.
Герман фон Гельмгольц

(1821 – 1894) и Джон Вильям Стретт (1842 – 1919) заложили фундамент современной музыкальной акустики.
Джордж Стокс (1819 – 1903) показал, насколько слабо передаются в окружающее пространство колебания поверхности струны.
А.М. Мейер в 1876г. описал так называемое явление маскировки.
Слайд 11Заключение
Со временем древних греков история музыкальной акустики была полна поисками музыкальных

строев, пригодных как для инструментов со свободной интонировкой, так и для инструментов с фиксированным звукорядом – например у клавишных, струнных и у язычковых инструментов.
Уже в древние времена греки предложили музыкальную шкалу, основанную на делении струны в кратном отношении. Но даже сами изобретатели этой системы, философы школы Пифагора, вряд ли слышали хоть один инструмент, в котором была бы реализована их система музыкального строя.










 ПЕДАГОГИКА ПОДДЕРЖКИ РЕБЕНКА И ПРОЦЕСС ЕГО РАЗВИТИЯ В СИСТЕМЕ ЛИЧНОСТНО-ОРИЕНТИРОВАННОГО ВОСПИТАНИЯ
ПЕДАГОГИКА ПОДДЕРЖКИ РЕБЕНКА И ПРОЦЕСС ЕГО РАЗВИТИЯ В СИСТЕМЕ ЛИЧНОСТНО-ОРИЕНТИРОВАННОГО ВОСПИТАНИЯ Лас су желісі. Канализация құбырлары мен коллекторларының кесінді қималары
Лас су желісі. Канализация құбырлары мен коллекторларының кесінді қималары Career in law abroad
Career in law abroad  ТЕМА : ГЛАГОЛ
ТЕМА : ГЛАГОЛ Технология обработки сырья и приготовления блюд
Технология обработки сырья и приготовления блюд Prezentare (2)
Prezentare (2)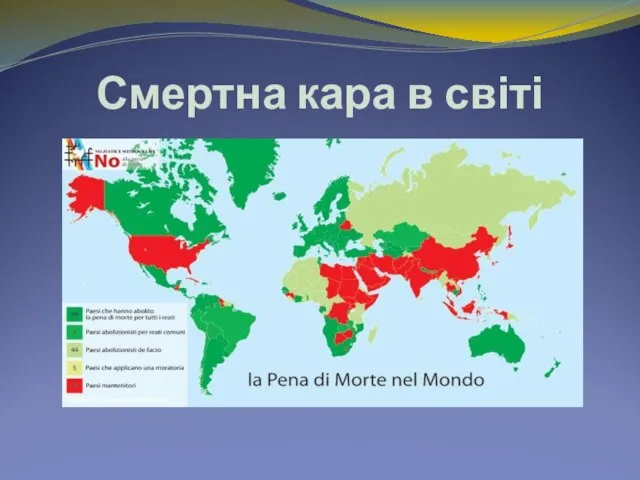 Смертная карта
Смертная карта  Центр независимых судебных экспертиз ТЕХЭКО
Центр независимых судебных экспертиз ТЕХЭКО Изложение Птицы говорят спасибо
Изложение Птицы говорят спасибо Классификация стиральных порошков
Классификация стиральных порошков Утомление при физической и умственной работе восстановление
Утомление при физической и умственной работе восстановление Презентация на тему МАТЕМАТИКА 1 КЛАСС
Презентация на тему МАТЕМАТИКА 1 КЛАСС  Презентация на тему Загадочная Намибия Племя Химба
Презентация на тему Загадочная Намибия Племя Химба  Слайд 1
Слайд 1 Правила делового этикета: как не ударить в грязь лицом
Правила делового этикета: как не ударить в грязь лицом Проект воздухоразделительной установки №7 в условиях АО Уральская Сталь
Проект воздухоразделительной установки №7 в условиях АО Уральская Сталь «Рио+20», устойчивое развитие и торговля
«Рио+20», устойчивое развитие и торговля Поэтам и писателям. Нургисаева Айжана
Поэтам и писателям. Нургисаева Айжана Проверка парных согласных и безударных гласных в корне слова
Проверка парных согласных и безударных гласных в корне слова Картины художников-передвижников
Картины художников-передвижников Информационные системы
Информационные системы Проведение сертификационных испытаний на отсутствие НДВ. Можно ли найти НДВ?
Проведение сертификационных испытаний на отсутствие НДВ. Можно ли найти НДВ? Инфекция мочевыводящих путей у беременных
Инфекция мочевыводящих путей у беременных Политический режим
Политический режим Московский Городской Педагогический УниверситетФакультет специальной педагогики
Московский Городской Педагогический УниверситетФакультет специальной педагогики Базиликовый соус Суго
Базиликовый соус Суго Семинар заместителей директоров по учебно-воспитательной работе:
Семинар заместителей директоров по учебно-воспитательной работе: История школьного портфеля
История школьного портфеля