Математические аспекты КГ. Аффинная и перспективная геометрия

Аффинные преобразования
Преобразование плоскости называется аффинным, если оно взаимно однозначно и образом любой прямой является прямая. Преобразование называется взаимно однозначным, если оно разные точки переводит в разные, и в каждую точку переходит какая-то точка.
Движения — это такие преобразования, которые сохраняют расстояние между любыми двумя точками неизменным, а именно параллельные переносы, повороты, различные симметрии и их комбинации.

Аффинные преобразования
Множество движений есть подмножество множества аффинных преобразований.

Аффинные преобразования
Аффинное преобразование является комбинацией линейных преобразований, сопровождаемых переносом изображений.

Перспективные преобразования
В перспективной геометрии нет двух линий, параллельных друг другу.
Перспективное преобразование имеет место в случае, когда последний столбец обобщенной матрицы преобразования 4×4 ненулевой.

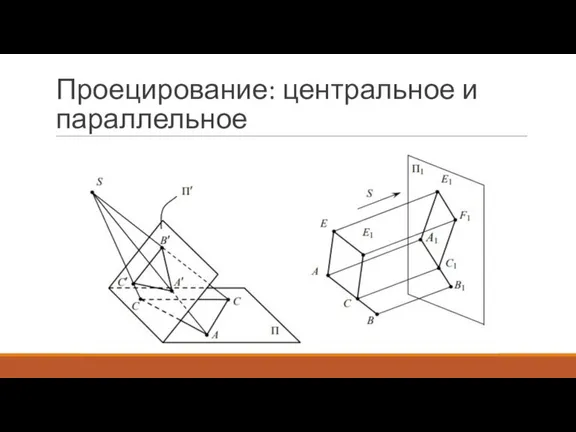
Проецирование: центральное и параллельное

Ортографические проекции

Ортографические проекции

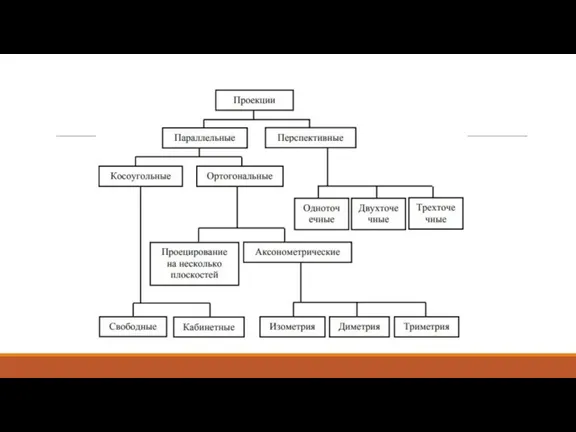
Аксонометрические проекции
Аксонометрическая проекция получается с помощью аффинного преобразования, определитель которого равен нулю.
изометрия – в плоскости проекции углы между каждой парой осей равны
диметрия – в плоскости проекции равны между собой два угла между осями
триметрия – в плоскости проекции все три угла между осями различны.

Аксонометрические проекции: пример 0
Единичный вектор оси Х, равный [1 0 0 1], преобразуется к виду
Единичный начальный вектор оси Х будет иметь длину

Аксонометрические проекции: пример 0
Для единичного вектора по оси Y [0 1 0 1]
Для того чтобы создать диметрическую проекцию, значения двух преобразованных единичных векторов сокращают в равное число раз.
Если выбранное значение угла Φ удовлетворяет уравнению, с помощью матрицы выполняют диметрическое проецирование.

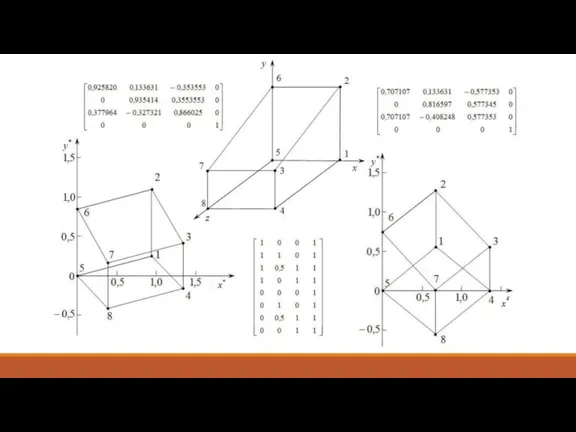
Аксонометрические проекции: пример 1
Для изометрического преобразования нужно в одинаковое число раз сократить все три оси. Для этого необходимо, чтобы выполнялись соотношения

Аксонометрические проекции: пример 1
Угол, который проекционная ось Х составляет с горизонталью, определяется соотношением

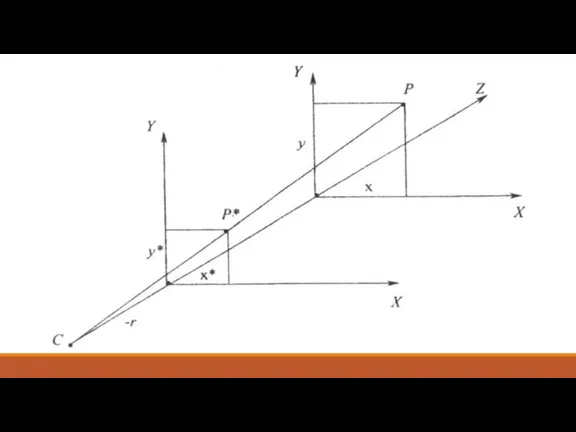
Перспективные преобразования
В матрице преобразования 4×4 ненулевые элементы в первых трех строках последнего столбца осуществляют перспективное преобразование.
Для плоскости z = 0

Перспективные преобразования
При z = 0 x* = x и y* = y. Вследствие этого преобразования точки, расположенные в плоскости наблюдения z = 0, при перспективном проецировании не изменяются. Однако это справедливо только в том случае, когда однородная координата Н является единичной и преобразования применяются к точке [x y z 1].

Перспективные преобразования
Одноточечные(параллельные) перспективные преобразования:
Точка схода перспективного преобразования – точка, через которую будут проходить изначально параллельные оси линии.

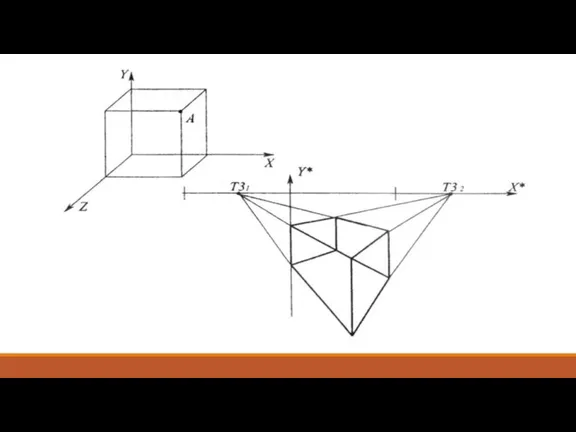
Перспективные преобразования:
пример
вращение куба вокруг оси Y и смещение к точке [0 m n]
«наблюдение» из точки k, расположенной на оси Z (точка схода)
проекция на плоскость z = 0

Стереографические проекции

Стереографические проекции
Чтобы выдержать точное значение стереоугла, требуется величина d=k/10. При создании перспективного изображения для левого глаза требуется горизонтальное смещение объекта на +d/2 = +k/20, а для правого глаза необходимо горизонтальное смещение на –d/2 = –k/20.