Математические софизмы

Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
Особенно часто в софизмах выполняют "запрещенные" действия или не учитываются условия применимости теорем, формул и правил.
Математические софизмы
Софизм- формально кажущееся правильным, но по существу ложное умозаключение, основанное на неправильном подборе исходных положений (словарь Ожегова)

В Греции софистами называли и простых ораторов- философов-учителей, задачей которых было научить своих учеников «мыслить, говорить и делать».
Их задачей обычно было научить убедительно защитить любую точку зрения.
А теперь немного истории…

арифметические
геометрические
алгебраические

Алгебраические софизмы.
Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.

«Два неодинаковых натуральных числа равны между собой»
решим систему двух уравнений
Сделаем это подстановкой у из 2-го уравнения в 1, получаем х+8-х=6, откуда 8=6
Где ошибка
Уравнение (2) можно записать как х+2у=8, так что исходная система запишется в виде:
Х+2у=6, Х+2у=8
В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения. Графически это означает, что прямые
у=3-х/2 и у=4-х/2 параллельны и не совпадают.
Перед тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.

«Уравнение x-a=0 не имеет корней»
Дано уравнение x-a=0. Разделив обе части этого уравнения на x-a, получим, что 1=0. Поскольку это равенство неверное, то это означает, что исходное уравнение не имеет корней.
Где ошибка?
Поскольку x=a – корень уравнения, то, разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому получили неверное равенство 1=0.

«Все числа равны между собой»
.
возьмём числа a < b,
тогда существует такое c > 0, что: a + c = b
умножим обе части на (a − b), имеем: (a + c)(a − b) = b(a − b)
a2 + ca − ab − cb = ba − b2
cb переносим вправо, имеем:
a2 + ca − ab = ba − b2 + cb
a(a + c − b) = b(a − b + c) отсюда a = b
Где ошибка?
По определению : a + c = b
Значит, a + c − b = 0
И выражение a(a + c − b) = b(a + c − b)
Тождественно a ∙ 0 = b ∙ 0.

Арифметика - (греч. arithmetika, от arithmys — число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы?
Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.

«Дважды два - пять»
Напишем тождество 4:4=5:5.
Вынесем из каждой части тождества общие
множители за скобки, получаем: 4(1:1)=5(1:1) или
Так как 1:1=1, то сократим и получим
Где ошибка?
Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой. Действительно, 4:4=1:1, но 4:4≠4(1:1).

«Пять равно шести»
Возьмем тождество 35+10-45=42+12-54.
В каждой части вынесем за скобки общий множитель:
5(7+2-9)=6(7+2-9).
Теперь, получим, что 5=6.
Где ошибка?
Ошибка допущена при делении верного равенства 5(7+2-9)=6(7+2-9) на число
7+2-9, равное 0. Этого нельзя делать.
Любое равенство можно делить только на число, отличное от 0.

«Один рубль не равен ста копейкам»
Известно, что любые два равенства можно перемножить почленно, не нарушая при этом равенства, т. е.если
а = b и c = d, то ac = bd.
Применим это положение к двум очевидным равенствам: 1 рубль = 100 копейкам и
10 рублей = 1000 копеек
Перемножая эти равенства почленно, получим
10 рублей = 100 000 копеек
и разделив последнее равенство на 10, получим, что
1 рубль = 10 000 копеек
Таким образом,
один рубль не равен ста копейкам.

«Один рубль не равен ста копейкам»
Где ошибка?
Ошибка, допущенная в этом софизме, состоит в нарушении правила действий с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.

Геометрические софизмы
Это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или противоречивое утверждение, связанное с геометрическими фигурами и действиями над ними

.
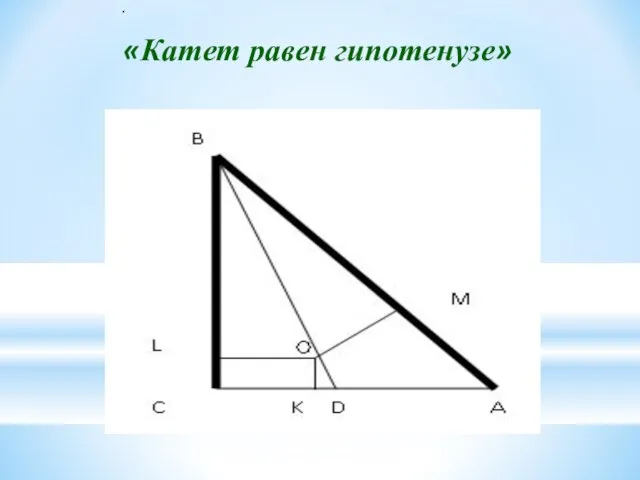
«Катет равен гипотенузе»

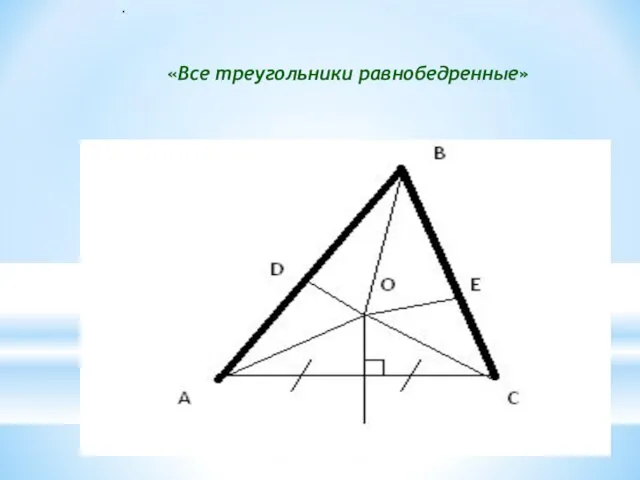
«Все треугольники равнобедренные»
.

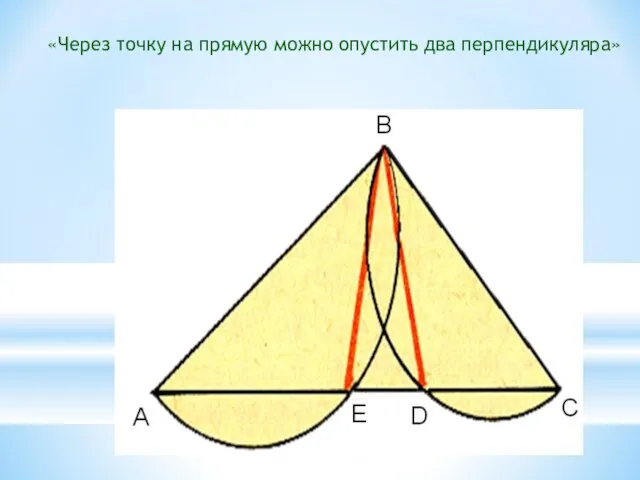
«Через точку на прямую можно опустить два перпендикуляра»

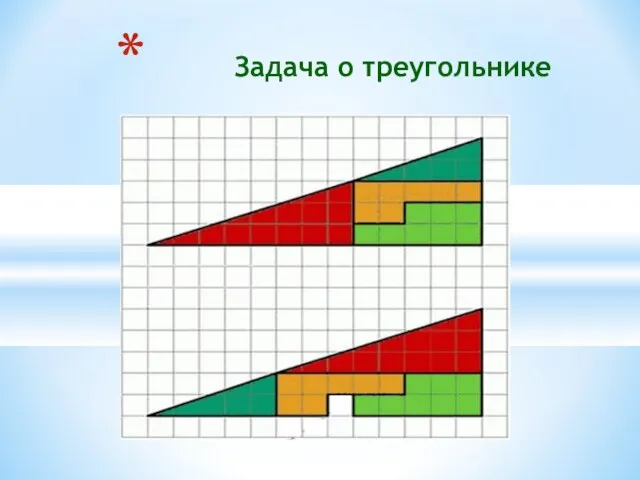
Задача о треугольнике