Математика вокруг нас

Цель проекта:
показать широту применения математики в обычных сферах жизни;
выявить сферы применения предложенных типов задач;
развивать познавательную активность обучающихся;
прививать интерес к предмету.

В любой задаче есть условие, т.е. исходные данные, заключение, т.е. требование, которое должен выполнить субъект.
Задача – это задание, которое должен выполнить субъект, или вопрос, на который он должен найти ответ, опираясь на указанное условие и все вытекающие из них следствия.
?

Суть арифметического метода состоит в том, что задачи решаются по действиям.
АЛГЕБРАИЧЕСКИЙ СПОСОБ РЕШЕНИЯ
Суть алгебраического метода решения задач состоит в том, что одна из величин принимается, например за х, все зависимости существующие между величинами переводятся на язык равенств, уравнений и далее решается полученное уравнение. Здесь мы предполагаем, что искомая величина найдена и оперируем ей как известной величиной. После нахождения х полученные результаты переводятся с математического языка на естественный.
АРИФМЕТИЧЕСКИЙ СПОСОБ РЕШЕНИЯ

Математика
Повседневная жизнь
Торговля
Финансовая
сфера
Статистика
Движение
Строительство

№1 Дорога в школу…
Маша и Андрей живут в одном доме. Маша вышла из дома и направилась в школу. Через четыре минуты после неё из дома вышел Андрей и догнал Машу у школы. Найдите расстояние от дома до школы, если Маша шла со скоростью 60 м/мин, а скорость Андрея 80 м/мин.
80 м/мин
60 м/мин

Решение.
Пусть х м-расстояние от дома до школы , тогда
х х
60 мин – время движения Маши , 80 мин – время движения Андрея.
В задаче известно , что через 4 минуты после Маши вышел Андрей и догнал её у школы.
Имеем уравнение:
х _ х
60 80 = 4 * 240
4х – 3х = 960
х = 960
Ответ:960 метров или 0,96 км – расстояние от дома школы.

№2 От Твери до Казани …
От Твери до Казани теплоход плывёт трое суток. А от Казани до Твери четверо суток. Чему равно время движения плота от Твери до Казани?

3 суток Казань
Тверь t - ? 4 суток
Решение:
Пусть х км/ч скорость плота, а у км/ч собственная скорость теплохода. (у + х) км/ч скорость теплохода по течению реки, (у – х) км/ч скорость теплохода против течения.
В задаче известно, что теплоход по течению шёл 3 суток или 72 часа. Имеем уравнение: (у +х) 72 = 1
Далее, известно, что против течения теплоход шёл 4 суток или 96 часов. Имеем уравнение: (у – х) 96 = 1.
Составим систему уравнений:
(у +х) 72 = 1 24у = 168х 1/х = 576
(у – х) 96 = 1 у = 7х 576 часов = 24 сут.
72у + 72х = 96у – 96х 72(7х + х) = 1
96у – 72у = 72х + 96х 576х = 1
Ответ: 24 суткам равно время движения плота от Твери до Казани.

Грузовой и легковой автомобили выехали одновременно навстречу друг другу соответственно из пунктов А и В. После встречи грузовой автомобиль прибывает в В через два часа, а легковой в А через 9/8 часа. Каждый едет с постоянной скоростью без остановки и, приехав в конечный пункт, тут же поворачивает обратно, и на обратном пути встречаются в 60 км от В. Найти время затраченное каждым автомобилем на поездку туда и обратно.
№3 Грузовик и легковушка…

Решение.
Пусть скорость грузового автомобиля V1 км/ч, скорость легкового автомобиля V2 км/ч, а расстояние от А до В равно S км.
После встречи грузовой автомобиль прибывает в B через 2 ч, легковой автомобиль в А через 9/8 ч
Приехав в конечный пункт, они тут же поворачивают обратно, и на обратном пути встречаются в 60 км.
Ответ: 7часов, 5 часов 15 минут.

№1 ДТП
В прошлом году в двух крупных городах области было зарегистрировано 900 дорожно-транспортных происшествий. В текущем году число ДТП в первом городе уменьшилось на 10%, во втором – на 30%, и всего в этих городах было зарегистрировано 740 случаев ДТП. Сколько происшествий было зарегистрировано в каждом из этих городов в прошлом году?

Решение.
Пусть х ДТП было в первом городе, а у ДТП было во втором городе. В задаче известно, что всего ДТП было 900.
Имеем уравнение: х + у = 900
Далее, 0,9х ДТП стало в первом городе, а 0,7у ДТП стало во втором городе. В задаче известно, что всего стало 740 ДТП.
Имеем уравнение: 0,9х + 0,7у = 740.
Составим систему:
х + у = 900 - 2х = - 1100 : (-2)
0,9х + 0,7у = 740 *10 х = 550
х + у = 900 *7 550 + у = 900
9х + 7у = 7400 у = 900 - 550
у = 350
7х + 7у = 6300 Ответ: 550 ДТП; 350 ДТП.
9х + 7у = 7400

В прошлом году на два самых популярных факультета университета было подано 1100 заявлений. В текущем году число заявлений на первый из этих факультетов уменьшилось на 20%, а на второй увеличилось на 30%, причём всего было подано 1130 заявлений.
Сколько заявлений было подано на каждый из этих факультетов в текущем году?
№2 Университет

Решение.
Пусть х заявлений подано на первый факультет в прошлом году, тогда (1100 – х) заявлений подано на второй факультет в прошлом году.
0,8х заявлений подано на первый факультет в текущем году, 1,3(1100 – х) заявлений –на второй факультет .
В задаче известно, что в текущем году было подано 1130 заявлений.
Имеем уравнение:
0,8х +1,3 (1100 – х) = 1130 600*0,8= 480 (з)
0,8 х +1430 – 1,3 х = 1130 1130 – 480 = 650(з)
-0,5 х = - 300
х = 600
Ответ: 480 заявлений; 650 заявлений.

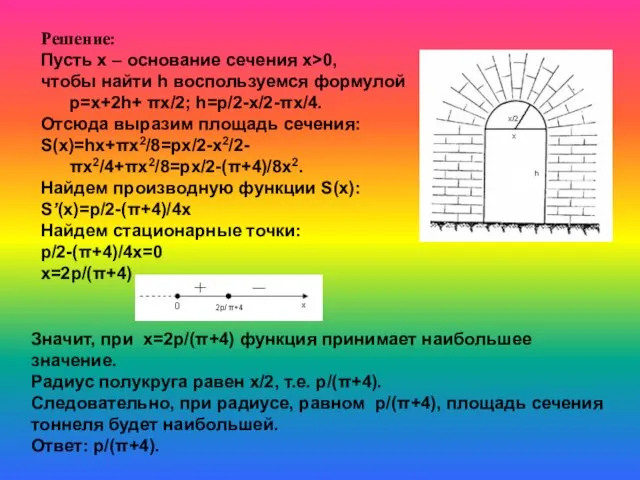
Сечение тоннеля имеет форму прямоугольника, сверху завершенного полукругом. Определить радиус полукруга, при котором площадь сечения будет наибольшей, если периметр сечения равен p.
№1 Туннель

Решение:
Пусть х – основание сечения x>0,
чтобы найти h воспользуемся формулой р=х+2h+ πх/2; h=р/2-х/2-πх/4.
Отсюда выразим площадь сечения:
S(x)=hx+πx2/8=px/2-x2/2-πx2/4+πx2/8=px/2-(π+4)/8x2.
Найдем производную функции S(x):
S’(x)=p/2-(π+4)/4x
Найдем стационарные точки:
p/2-(π+4)/4x=0
x=2p/(π+4)
Значит, при x=2p/(π+4) функция принимает наибольшее значение.
Радиус полукруга равен х/2, т.е. p/(π+4).
Следовательно, при радиусе, равном p/(π+4), площадь сечения тоннеля будет наибольшей.
Ответ: p/(π+4).

№2 Школьная площадка
Для школьной площадки выделен прямоугольный участок земли. Длина ограды вокруг площадки окажется меньше, если участок при той же площади будет иметь квадратную форму. Для этого надо одну сторону участка увеличить на 18 метров, а другую уменьшить на 27 метров. Какова сторона квадратного участка?

Решение.
Пусть х м сторона квадратного участка, тогда (х – 18) м ширина первоначального участка, а (х + 27) м длина первоначального участка.
(х - 18)(х +27) м² площадь первоначального участка.
В задаче известно, что площади этих двух участков равны.
Имеем уравнение:
х² = (х - 18)(х + 27)
х² = х² - 18х + 27х - 486
х² - х² +9х - 486 = 0
9х =486
х = 54
Ответ: 54 метра сторона квадратного участка.

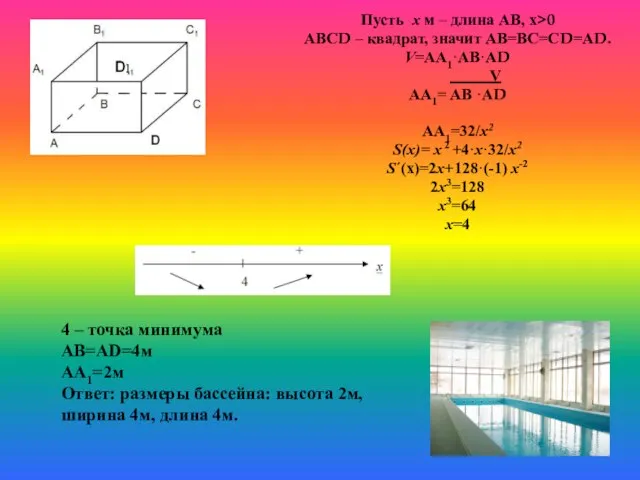
Определите размеры бассейна с квадратным дном и объёмом 32 м3 таким образом, чтобы на его отделку пошло как можно меньше плитки?
№3 Бассейн

Пусть х м – длина АВ, х>0
АВСD – квадрат, значит АВ=ВС=СD=АD.
V=AA1·АВ·АD
V
АА1= АВ ·АD
АА1=32/х2
S(х)= х 2 +4·х·32/х2
S´(х)=2x+128·(-1) x-2
2x3=128
x3=64
x=4
4 – точка минимума
АВ=АD=4м
АА1=2м
Ответ: размеры бассейна: высота 2м, ширина 4м, длина 4м.

Купол здания имеет форму конуса с радиусом основания 8/π м, а образующей 6м, решено обкладывать плиткой.
Сколько м2 плитки надо приобрести, если плитка покупается с запасом в 10%?
№4 Купола

Решение:
По условию дано, что R=8/π м и L=6м. Чтобы узнать, сколько м2 плитки необходимо приобрести, надо узнать площадь боковой поверхности купола.
Площадь боковой поверхности
такого конуса равна: S= πRL
S=π*8/ π*6=8*6=48м2
Нам сказано, что плитка покупается с запасом в 10%.
Значит, 48*0.1+48=4.8+48=52,8м2
Ответ: надо приобрести 52,8 м2 плитки.

№1 Банковский счет
На банковский счет было положено 10 тыс. руб. После того, как деньги пролежали один год со счета сняли 1 тыс. руб. Еще через год на счету стало 11 тыс. руб. Определить, какой процент годовых начисляет банк.

Решение.
Пусть банк начисляет р% годовых.
1) Сумма в 10000 рублей, положенная на банковский счет под р% годовых, через год возрастет до величины
10000 + 0,01×p× 10000 = 10000 + 100р (руб).
Когда со счета снимут 1000 руб., там останется 9000 + 100р (руб).
2) Еще через год последняя величина за счет начисления процентов возрастет до величины
9000 + 100р + 0,01p(9000 + 100р) = р2 + 190р + 9000 (руб).
По условию эта величина равна 11000 руб.
р2 + 190р + 9000 = 11000;
р2 + 190р - 2000 = 0.
Решим это квадратное уравнение, используя теорему Виета, p1 = 10, p2 = -200.
Отрицательный корень не подходит.
Ответ. 10%.

№1 Изменение стоимости
Первоначальная стоимость товара равнялась 75 руб. В течение первого года она повысилась на некоторое число процентов, а в течение второго года снизилась (по отношению к повышенной стоимости) на такое же число процентов, в результате чего она стала равна 72 руб. Определите проценты повышения и понижения стоимости товара.

Решение.
Пусть х% - это проценты повышения (и понижения) стоимости товара. По определению х% от 75 это — 75×0,01x. Тогда после первого повышения цена станет равняться (75 + 0,75x) руб.
В течение второго года цена снизится на величину
0,01x(75+0,75х) = (0,75х + 0,0075х2) руб.
Теперь можно записать уравнение для окончательной цены
(75 + 0,75х) - (0,75х + 0,0075х2) = 72;
х2 = 400; отсюда x1 = - 20, x2 = 20.
Подходит только один корень этого уравнения: х2 = 20.
Ответ: 20%.

№1 Грибы
Влажность свежих грибов 90%, а сухих – 15%. Сколько сухих грибов получится из 1,7 кг свежих?

Решение.
Сколько процентов свежих грибов составляет масса без воды?
100 – 90 = 10%
Свежие грибы – 1,7кг 100%
Масса без воды - х кг 10%
Составим пропорцию:
1,7 : х = 100 : 10
х = 1,7 *10 : 100
х = 0,17 кг
Сколько процентов сухих грибов составляет масса без воды?
100 – 15 = 85%
Сухие грибы – у кг 100%
Масса без воды - 0,17 кг 85%
Составим пропорцию:
у :0,17 = 100 : 85
у = 0,17 *100 : 85
у = 0,2 кг
Ответ: 200 г сухих грибов получится из 1,7 кг свежих.

№2 Два мастера
Два мастера оклеили обоями квартиры на этаже в новом доме за 15 дней, причём второй присоединился к первому через 7 дней после начала работы. Известно, что первому мастеру на выполнение всей работы потребовалось бы на 7 дней меньше, чем второму. За какое время мог бы выполнить эту работу каждый мастер, работая отдельно?

Решение.
Пусть х дней потратил бы на выполнение всей работы первый мастер, х>0, тогда (х + 7) дней – второй рабочий.
1/х – производительность труда первого рабочего, а 1/(х +7) – производительность труда второго рабочего.
В задаче известно, что первый мастер работал 15 дней, а второй 8 дней и выполнили вместе всю работу.
Имеем уравнение:
15 8
х + х +7 = 1 *х(х+7)
15х + 105 + 8х = х2 + 7х
х2 – 16х – 105 = 0
х = 21 и х = - 5
21 +7 =28 дней
Ответ: 21 день, 28 дней.

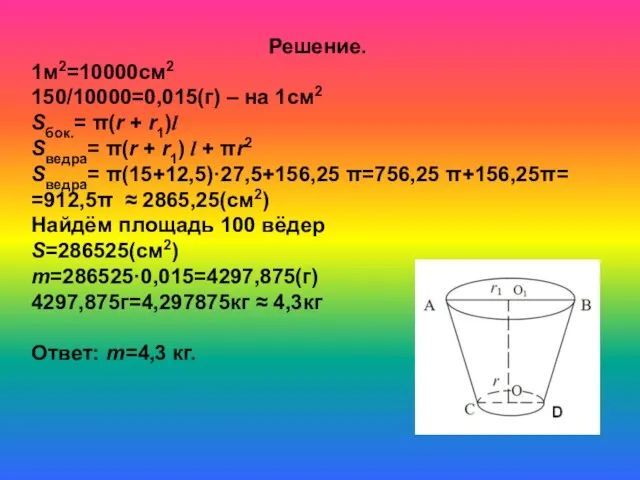
№3 Вёдра
Сколько олифы потребуется для окраски 100 вёдер в форме усечённого конуса, диаметры ведра 30см и 25 см, а образующая 27,5см, если на 1м2 надо 150 г олифы?

Решение.
1м2=10000см2
150/10000=0,015(г) – на 1см2
Sбок.= π(r + r1)l
Sведра= π(r + r1) l + πr2
Sведра= π(15+12,5)·27,5+156,25 π=756,25 π+156,25π= =912,5π ≈ 2865,25(см2)
Найдём площадь 100 вёдер
S=286525(см2)
т=286525·0,015=4297,875(г)
4297,875г=4,297875кг ≈ 4,3кг
Ответ: т=4,3 кг.