Mat_Modelirovanie_-_1

Основные понятия и характеристика пласта
Фильтрацией называется движение жидкостей, газов, их смесей в пористых и трещиноватых средах, то есть в твердых телах,
системой сообщающихся
между
газов
по сравнению
собой пор и
с
пронизанных микротрещин. движением
Фильтрация жидкостей и
в трубах и каналах
обладает
специфическими
некоторыми особенностями: происходит по чрезвычайно
малым в поперечных размерах поровым каналам при очень малых
движения жидкостей;
силы
трения
скоростях
жидкости в
пористой среде очень велики, так
при движении
как площади
огромны.
соприкосновения жидкости с твердыми частицами
Коэффициентом пористости m называется
отношение
объема пор в образце Vп к объему образца V:
m=Vп/V
Коэффициент пористости выражается в долях
единицы
или в
к объему образца.
Определение
коэффициента
необходимо для
процентах пористости процессов
фильтрации
оценки запасов
в
пористой
нефти и изучения
среде.

Основные понятия и характеристика пласта
Коэффициентом просветности n называется отношение площади просветов ωпр в данном сечении пористой среды ко всей площади этого сечения ω:
n=ωпр/ω
Площадь просветов различна в различных поперечных сечениях ωпр(х).
Поперечным сечением ω называется поверхность,
проведенная перпендикулярно направлению скорости.
жидкости,
Объемным расходом Q называется объем
прошедший через поперечное сечение за единицу времени:
Q=V/t
жидкости,
Массовым расходом Qm называется масса
прошедшая через поперечное сечение за единицу времени:
Qm=m/t

Основные понятия и характеристика пласта
Массовый расход равен произведению плотности ρ на объемный расход:
Qm=ρ·Q
Скоростью фильтрации u называется отношение объемного расхода жидкости к площади поперечного сечения:
u=Q/ω
В действительности фильтрация жидкости или газа происходит по просветам, поэтому действительная скорость v определяется по следующей формуле:
v=u/m

Закон Дарси
В основе математической формулировки всякой физической задачи должен лежать какой-либо основной закон, устанавливающий вид связи между изучаемыми величинами. В теории фильтрации одним из таких основных законов, является закон Дарси.
Закон Дарси – устанавливает связь между величиной скорости фильтрации вдоль линии тока и силами, действующими в жидкости.
его способность
Проницаемость коллектора – параметр, характеризующий пропускать жидкость или газ при перепаде
давления. Как и пористость, проницаемость не постоянная величина
и изменяется по площади пласта и по напластованию.
Для характеристики проницаемости пород нефтесодержащих пластов введены понятия абсолютной, фазовой и относительной проницаемости.

Закон Дарси
Для оценки проницаемости
горных
пород
обычно
пользуются
жидкости в единицу времени, м3/с;
μ – динамическая
жидкости, Па·с; F – площадь фильтрации, м2;
вязкость ΔР – перепад
Физический смысл размерности коэффициента
проницаемости
– это величина площади сечения каналов пористой среды горной
породы, по которым происходит фильтрация флюидов.
линейным законом фильтрации Дарси, по которому скорость фильтрации жидкости в пористой среде пропорциональна градиенту давления и обратно пропорциональна динамической вязкости:
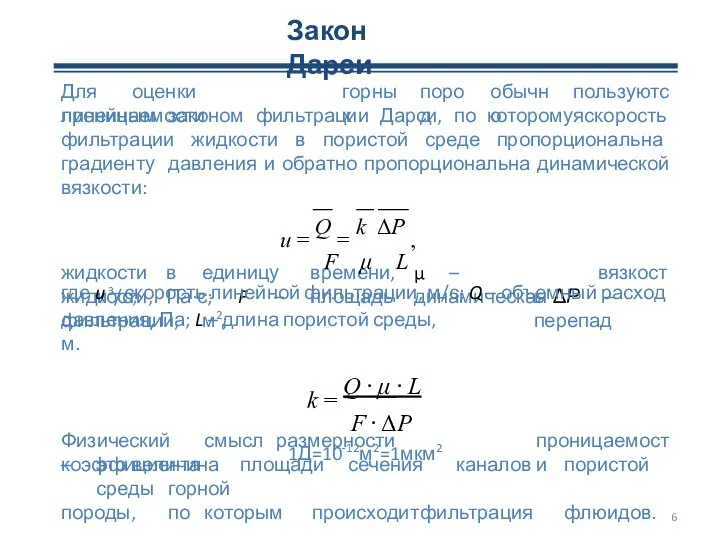
u = Q = k ΔP ,
F μ L
где u – скорость линейной фильтрации, м/с; Q – объемный расход
давления, Па; L – длина пористой среды, м.
k = Q ⋅ μ ⋅ L
F ⋅ ΔP
1Д=10-12м2=1мкм2

7
Нарушение закона Дарси.
Нелинейные законы фильтрации
Подобно тому, как в трубной гидравлике критерием режима движения
служит число Рейнольдса –
критического (Reкр), которое устанавливается из опыта.
Re = υdρ / μ
в теории фильтрации вводится безразмерный параметр – Re = uaρ / μ, где u - некоторая характерная скорость; a - линейный параметр, характеризующий среднее сечение поровых каналов; ρ - плотность жидкости; μ - динамический коэффициент вязкости.
Скорость фильтрации, при которой нарушается закон Дарси, называется критической скоростью фильтрации (uкр ).
Однако нарушение линейного закона фильтрации еще не означает перехода от ламинарного движения к турбулентному. Закон Дарси нарушается вследствие того, что силы инерции, возникающие в жидкости за счет извилистости каналов и изменения площади их поперечных сечений, становятся при u>uкр соизмеримыми с силами трения.
В трубной гидравлике значение Re, при котором происходит смена режимов, равно Reкр = 2320, в теории фильтрации закон Дарси имеет место при значении безразмерного параметра Re, меньшего

Нарушение закона Дарси.
Нелинейные законы фильтрации
Впервые число Рейнольдса для фильтрации жидкости было введено Н.Н.Павловским в виде:
пропорциональное корню квадратному из коэффициента проницаемости
Число Рейнольдса по В.Н.Щелкачеву имеет вид
а критические значения лежат в интервале l
Re =
(0,75m + 0,23)μ
udэρ
a =
dэ
0,75m + 0,23
Критические значения Re по Павловскому заключены в интервале:
Reкр = 7,5 ÷ 9
В.Н.Щелкачев предложил взять за линейный параметр выражение,
а =10 km−2,3
m2,3μ
Re = 10u kρ

Нарушение закона Дарси.
Нелинейные законы фильтрации
По М.Д.Миллионщикову за характерную скорость
взята
действительная скорость движения жидкости, а за линейный параметр
– выражение
кр
- 0,022 < Re < 0,29.
Если вычисленное по одной из вышепредставленных формул значение числа Re оказывается меньше нижнего критического значения Reкр, то закон Дарси справедлив, если Re больше верхнего значения Reкр, то закон Дарси заведомо нарушен.
Определение режима фильтрации жидкостей и газов имеет большое практическое значение, ибо без знания закона фильтрации в пласте нельзя правильно рассчитать дебиты скважин, распределение давления в пласте, а также невозможно определение параметров пласта по данным исследования нефтяных и газовых скважин.
m μ
m1,5 μ
k , т.е. Re = υ k / mρ = u k ρ

Нарушение закона Дарси.
Нелинейные законы фильтрации
двучленной формулой
имеют один и тот же порядок; при больших скоростях
,
что соответствует квадратичному закону сопротивления и имеет место при фильтрации в крупнозернистых и трещиноватых породах. Формула называется формулой А.А. Краснопольского.
При нарушении закона Дарси зависимость между скоростью фильтрацииu и градиентом давления dp/ ds лучше всего описывается
dp = au + bu 2
ds
которая выражает плавный переход от линейного закона фильтрации к
нелинейному. При малых значениях скоростиau >> bu2 пренебрегаем
вторым членом и получаем закон Дарси; при значениях u ≥ uкрслагаемые
au и bu2
фильтрации au << bu2 и можно принять
ds
dp = bu2
a = μ/ k
63⋅106
b = ρ(k / m)3/ 2

Задачи
Задача 1
По керну диаметром 2 см, длиной 5 см за десять минут прокачано 0,6 см3 воды. Абсолютное давление на входе 0,5 МПа, а на выходе 0,2 МПа. Определить действительную скорость и скорость фильтрации на входе в керн, если пористость керна 10%.
Задача 2
Определить значение числа Рейнольдса у стенки гидродинамически несовершенной по характеру вскрытия нефтяной скважины, если известно, что эксплуатационная колонна перфорирована, на каждом метре длины колонны прострелено 10 отверстий диаметром d0=10 мм, толщина пласта h=15 м, проницаемость пласта k=1 мкм2, пористость его m=18%, коэффициент вязкости нефти µ=4 мПа∙с, плотность нефти ρ= 870 кг/м3 и дебит скважины составляет 140 м3/сут.
Задача 3
Определить по формуле Щелкачева, происходит ли фильтрация в пласте по закону Дарси, если известно, что дебит нефтяной скважины Q=200 м3/сут, толщина пласта h=5 м, коэффициент пористости m=16%, коэффициент проницаемости k=0,2 мкм2, плотность нефти ρ=0,8 г/см3, динамический
гидродинамически
11
коэффициент вязкости ее µ=5 мПа*с. Скважина совершенна, радиус ее rc=0,1 м.

План лекционного занятия
1. Основные понятия и характеристики пласта;
2. Закон Дарси;
3. Нарушение закона Дарси. Нелинейные законы фильтрации;
4. Исследование прямолинейно-параллельного установившегося фильтрационного потока несжимаемой жидкости в однородном пласте.