Решение задач с практическим содержанием

вступление
Зная принципы решения теоретических алгебраических и геометрических задач, можно применить их для достижения практически необходимых в жизни человека вещей. Начиная от постройки игрушечного домика и кончая моделированием и постройкой всевозможных аппаратов. С помощью этих знаний можно рассчитать минимальное или максимальное количество ресурсов, потребующихся для выполнения поставленной задачи. С помощью этого можно определить практические площади, объёмы, поправки, расстояния и т.д. Этот далеко не полный список показывает, как необходимо знание теоретических принципов на практике, и доказывает, как важно знание математики в жизни.

Задача 1.
а)
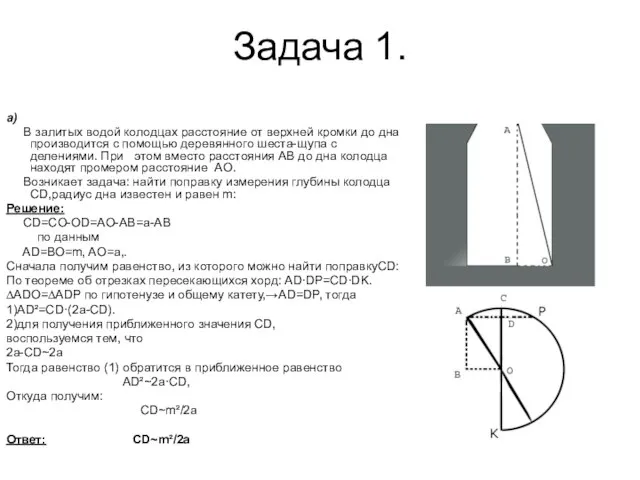
В залитых водой колодцах расстояние от верхней кромки до дна производится с помощью деревянного шеста-щупа с делениями. При этом вместо расстояния АВ до дна колодца находят промером расстояние AO.
Возникает задача: найти поправку измерения глубины колодца CD,радиус дна известен и равен m:
Решение:
CD=CO-OD=AO-AB=a-AB
по данным
AD=ВО=m, AO=a,.
Сначала получим равенство, из которого можно найти поправкуCD:
По теореме об отрезках пересекающихся хорд: AD∙DP=CD∙DK.
∆ADO=∆ADP по гипотенузе и общему катету,→AD=DP, тогда
1)AD²=CD·(2a-CD).
2)для получения приближенного значения CD,
воспользуемся тем, что
2a-CD~2a
Тогда равенство (1) обратится в приближенное равенство
AD²~2a·CD,
Откуда получим:
CD~m²/2a
Ответ: CD~m²/2a

Задача 1
б)
Найдём количество дней, на которые хватит полного колодца для семьи из 4 человек, при условии того, что суточная норма потребления воды каждого члена-10 литров, если известны радиусы дна и верхней кромки и высота колодца.
Решение: путем некоторых преобразований найдем объём колодца: Разделим колодец на 2 фигуры: усечённый конус и цилиндр, объемы, которых соответственно равны:
V2= (π/3) ·h2· ( r22+r32+r2 ·r3), и V1=π·r12 ·h1
Vоб =V1+V2
h2=√d²-(r2- r3)²,где d-длина скоса; h1=h- h2
Суточное потребление воды семьёй равняется 40 литров (10·4). Тогда количество дней будет вычисляться по формуле: V/40, то есть
((π/3) ·h2· ( r22+r32+r2 ·r3) + π·r12 ·h1)/40= n, где n- количество дней.
Ответ:
((π/3) ·h2· ( r22+r32+r2 ·r3) + π·r12 ·h1)/40= n

Задача 2.
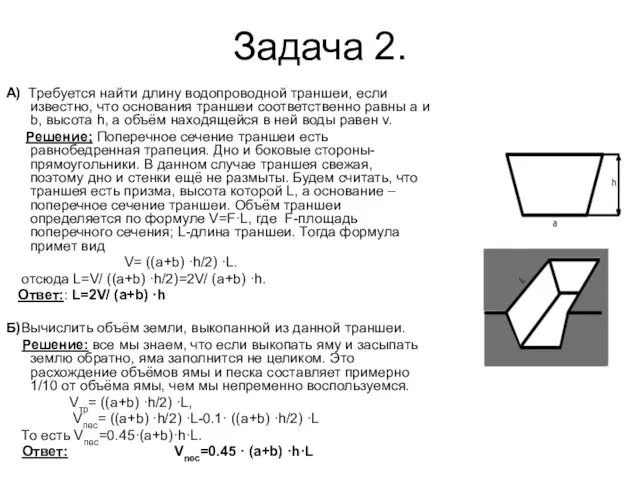
А) Требуется найти длину водопроводной траншеи, если известно, что основания траншеи соответственно равны a и b, высота h, а объём находящейся в ней воды равен v.
Решение; Поперечное сечение траншеи есть равнобедренная трапеция. Дно и боковые стороны- прямоугольники. В данном случае траншея свежая, поэтому дно и стенки ещё не размыты. Будем считать, что траншея есть призма, высота которой L, а основание – поперечное сечение траншеи. Объём траншеи определяется по формуле V=F·L, где F-площадь поперечного сечения; L-длина траншеи. Тогда формула примет вид
V= ((a+b) ·h/2) ·L.
отсюда L=V/ ((a+b) ·h/2)=2V/ (a+b) ·h.
Ответ:: L=2V/ (a+b) ·h
Б)Вычислить объём земли, выкопанной из данной траншеи.
Решение: все мы знаем, что если выкопать яму и засыпать землю обратно, яма заполнится не целиком. Это расхождение объёмов ямы и песка составляет примерно 1/10 от объёма ямы, чем мы непременно воспользуемся.
Vтр= ((a+b) ·h/2) ·L,
Vпес= ((a+b) ·h/2) ·L-0.1· ((a+b) ·h/2) ·L
То есть Vпес=0.45·(a+b)·h·L.
Ответ: Vпес=0.45 · (a+b) ·h·L

Задача 3
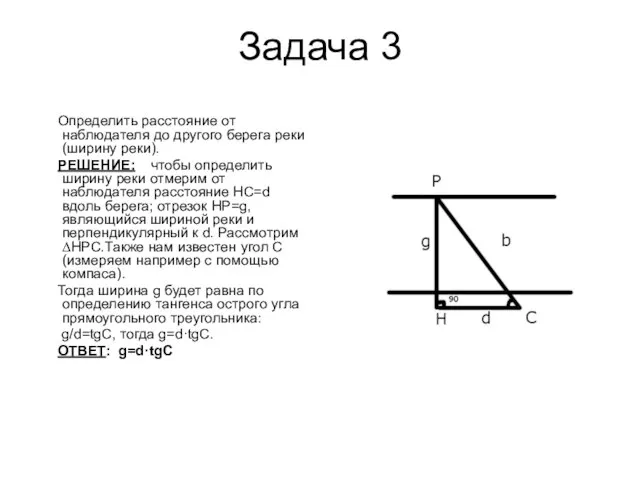
Определить расстояние от наблюдателя до другого берега реки (ширину реки). РЕШЕНИЕ: чтобы определить ширину реки отмерим от наблюдателя расстояние HC=d вдоль берега; отрезок HP=g, являющийся шириной реки и перпендикулярный к d. Рассмотрим ∆HPC.Также нам известен угол С(измеряем например с помощью компаса).
Тогда ширина g будет равна по определению тангенса острого угла прямоугольного треугольника:
g/d=tgС, тогда g=d·tgС.
ОТВЕТ: g=d·tgС

Задача 4
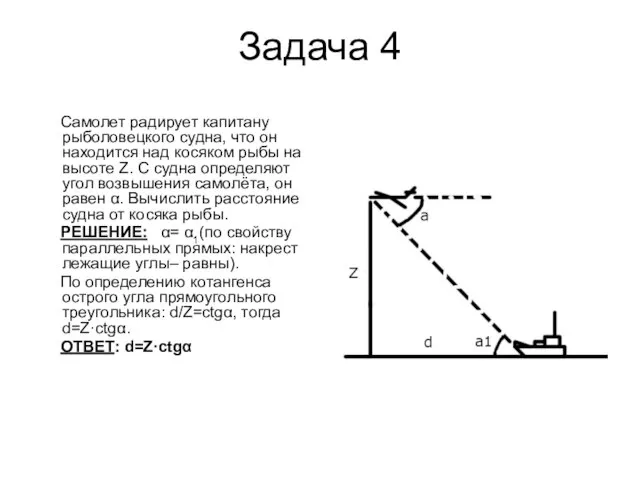
Самолет радирует капитану рыболовецкого судна, что он находится над косяком рыбы на высоте Z. С судна определяют угол возвышения самолёта, он равен α. Вычислить расстояние судна от косяка рыбы.
РЕШЕНИЕ: α= α1(по свойству параллельных прямых: накрест лежащие углы– равны).
По определению котангенса острого угла прямоугольного треугольника: d/Z=ctgα, тогда d=Z·ctgα.
ОТВЕТ: d=Z·ctgα

Задача 5
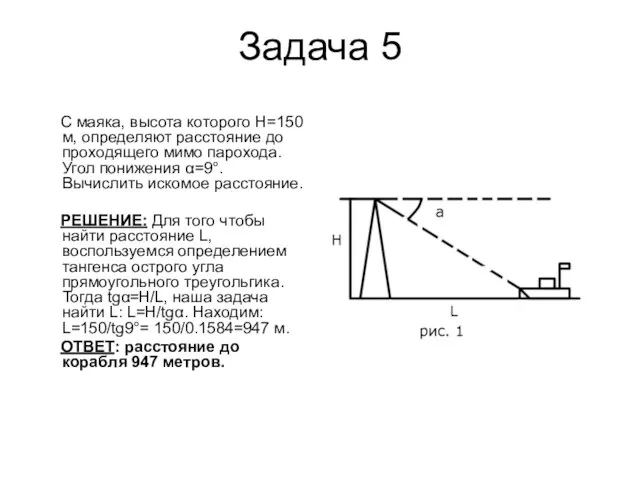
С маяка, высота которого Н=150 м, определяют расстояние до проходящего мимо парохода. Угол понижения α=9°. Вычислить искомое расстояние.
РЕШЕНИЕ: Для того чтобы найти расстояние L, воспользуемся определением тангенса острого угла прямоугольного треугольгика. Тогда tgα=H/L, наша задача найти L: L=H/tgα. Находим: L=150/tg9°= 150/0.1584=947 м.
ОТВЕТ: расстояние до корабля 947 метров.

Задача 6
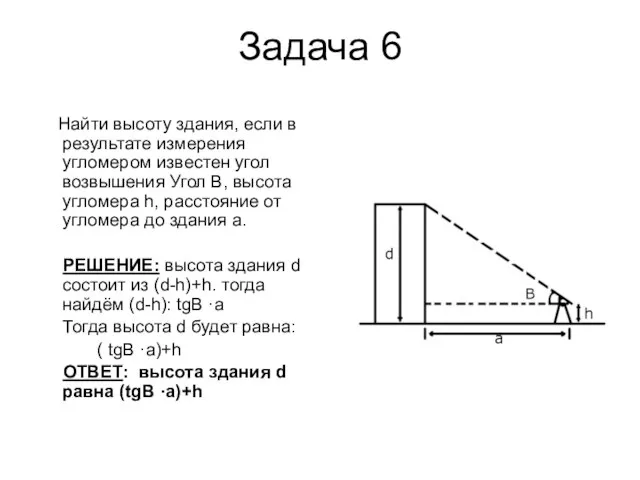
Найти высоту здания, если в результате измерения угломером известен угол возвышения Угол В, высота угломера h, расстояние от угломера до здания а.
РЕШЕНИЕ: высота здания d состоит из (d-h)+h. тогда найдём (d-h): tgB ·a
Тогда высота d будет равна:
( tgB ·a)+h
ОТВЕТ: высота здания d равна (tgB ·a)+h

Задача 7
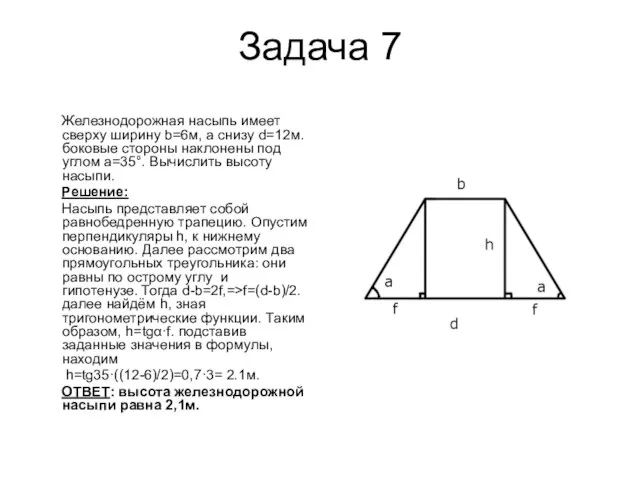
Железнодорожная насыпь имеет сверху ширину b=6м, а снизу d=12м. боковые стороны наклонены под углом a=35°. Вычислить высоту насыпи.
Решение:
Насыпь представляет собой равнобедренную трапецию. Опустим перпендикуляры h, к нижнему основанию. Далее рассмотрим два прямоугольных треугольника: они равны по острому углу и гипотенузе. Тогда d-b=2f,=>f=(d-b)/2. далее найдём h, зная тригонометрические функции. Таким образом, h=tgα·f. подставив заданные значения в формулы, находим
h=tg35·((12-6)/2)=0,7·3= 2.1м.
ОТВЕТ: высота железнодорожной насыпи равна 2,1м.

Задача 8
Две водопроводные трубы с диаметрами d нужно заменить одной большой трубой, но с той же пропускной способностью. Рассчитать диаметр D новой трубы.
РЕШЕНИЕ: так как новая труба имеет такую же пропускную способность, как и две первые, то, следовательно, она имеет такую же площадь сечения, как у двух первых:
S=2s.
Мы знаем, что s=πr², тогда 2s=2(πr²), или
2s=2(πd²/4) =πd²/2,
S=πD²/4,
тогда
πd²/2=πD²/4, или d²/2=D²/4,
отсюда следует, что
D²=4d²/2=2d², а D=d√ 2.
ОТВЕТ: D=d√ 2

Задача 9
Запроектирована водонапорная башня с металлическим баком на 100 м³. диаметр бака 5,5 м. найти высоту бака.
Решение: в данном баке нам дан диаметр 2r,а также его объём v=πr²h. Наша задача нахождение высоты бака. Найдём её по формуле:
h=v/πr².
Подставив в формулу известные величины, найдем:
h=100/ ((5, 5/2)²·3.14)= =100/23,74625~4,2 метра
ОТВЕТ: высота бака 4,2 метра