Содержание
- 2. Проекции преобразуют точки из координатной системы размерности n в точки координатной системы размерности меньше n.
- 3. Проекции строятся с помощью прямых линий – проекторов (лучи проекции), пересекающих поверхность проекции; оперируют с плоскими
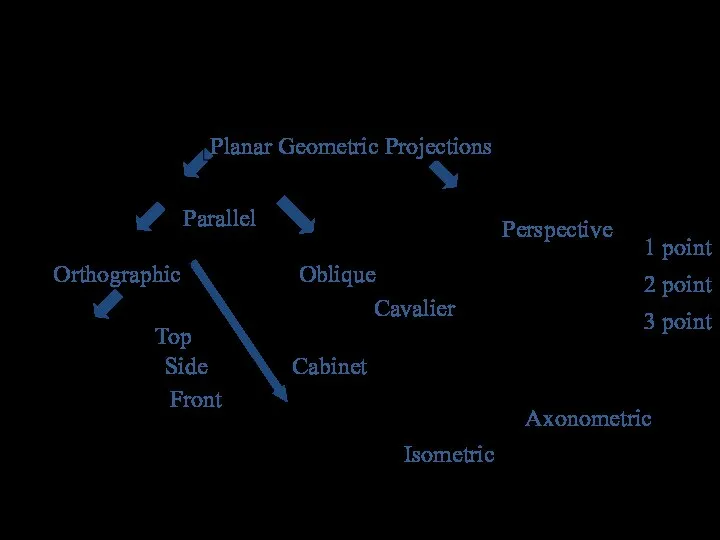
- 4. Классификация проекций ПРОЕКЦИИ одноточечные двухточечные трёхточечные Параллельные проекции Ортогональные Аксонометрические изометрия диметрия триметрия Косоугольные изометрия диметрия
- 5. Центральные проекции
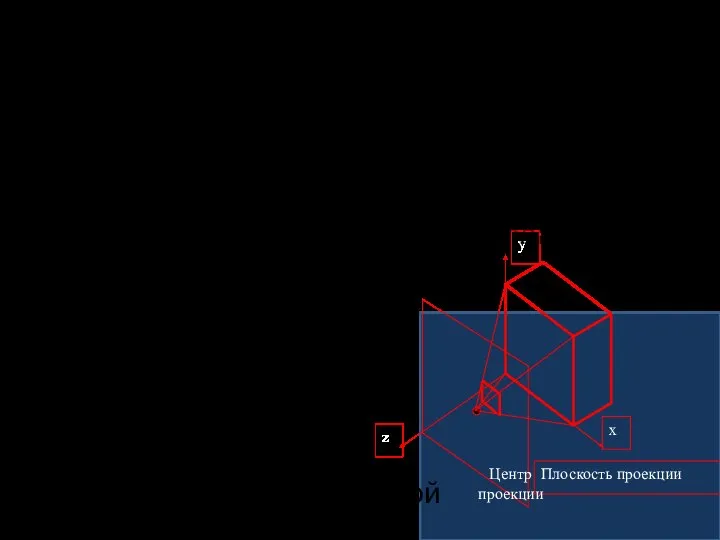
- 6. Центральные проекции Определяются плоскостью проекции и центром проекции. Визуальный эффект – перспективное искажение (перспектива). Размер проекций
- 7. Перспектива (Perspective) Первое изображение с перспективой – "Троица" Мазаччо, 1427г.
- 8. Центральные проекции Центральные проекции любой совокупности параллельных прямых, не параллельные проекционной плоскости, будут сходиться в центре
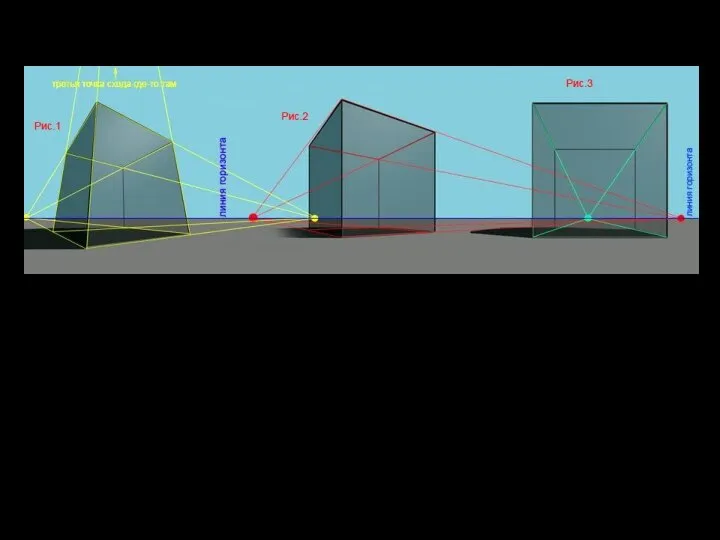
- 9. 1-точечная проекция Плоскость проекции пересекается только с одной осью. Точка схода в однородных координатах имеет w
- 10. 2-х точечная проекция Edward Hopper The Mansard Roof 1923 г.
- 11. 3-х точечная проекция Georgia O'Keefe «City Night»,1926 г.
- 12. Центральные проекции 3-х точечная 2-х точечная 1- точечная
- 13. Параллельные проекции
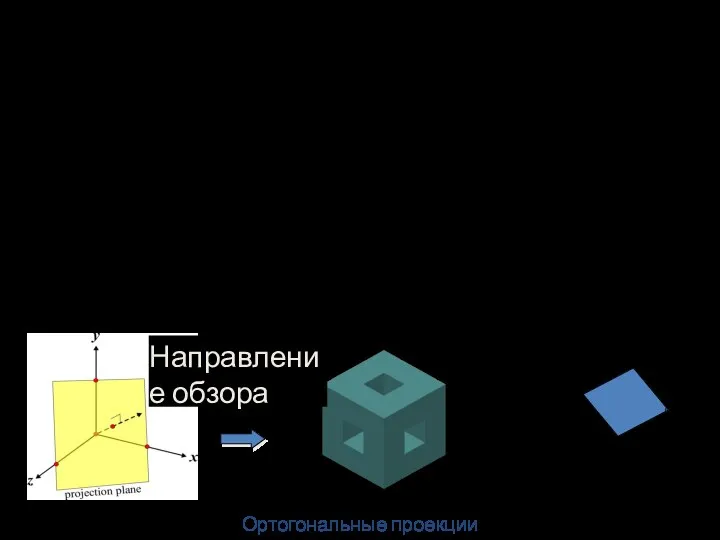
- 14. Ортогональные проекции Строится параллельным проецированием на плоскость отображения. Проецирующие лучи перпендикулярны к плоскости проекций. Обычно плоскость
- 15. Множественные проекции (Multiple Projections) Ортогональные проекции часто используются для построения множественных проекций объекта: вид сверху или
- 16. Проекционные плоскости не перпендикулярны осям координат. Одновременно видны несколько поверхностей объекта. Используется для измерений: углы изменяются;
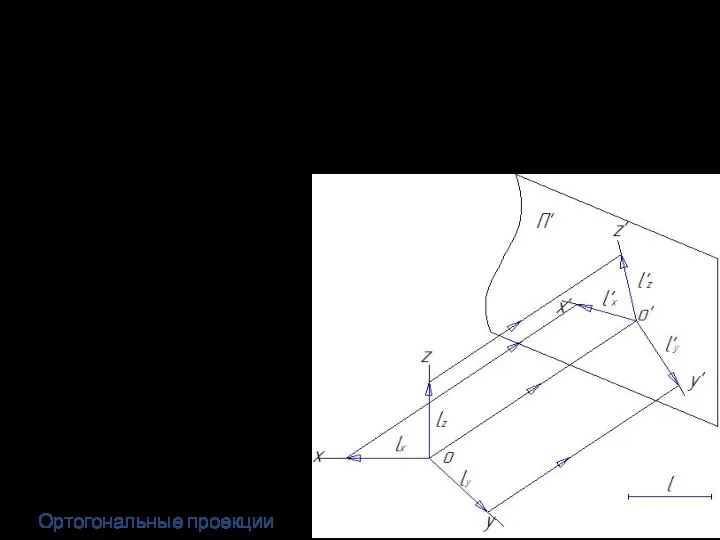
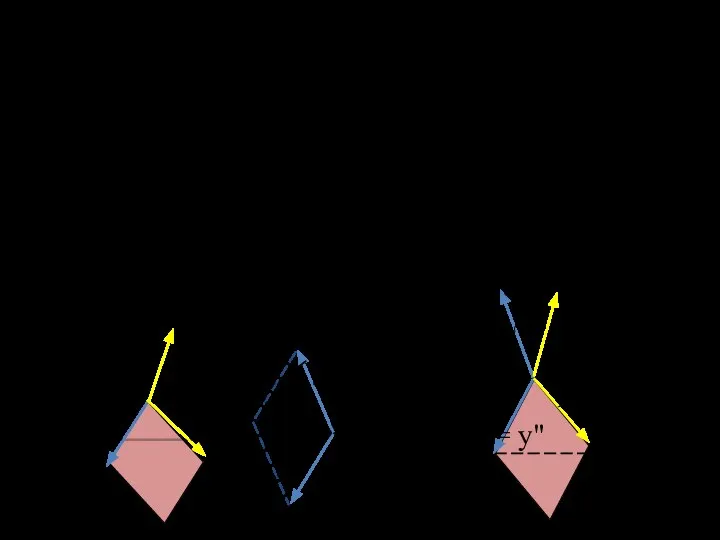
- 17. Основная теорема аксонометрии: теорема Польке: «три отрезка произвольной длины, лежащие в 1-й плоскости и выходящие из
- 18. Согласно этой теореме: любые три прямые в плоскости, исходящие из одной точки и не совпадающие между
- 19. Отношение единичных отрезков на аксонометрических осях к единичным отрезкам на координатных осях называется коэффициентом искажения (коэффициентом
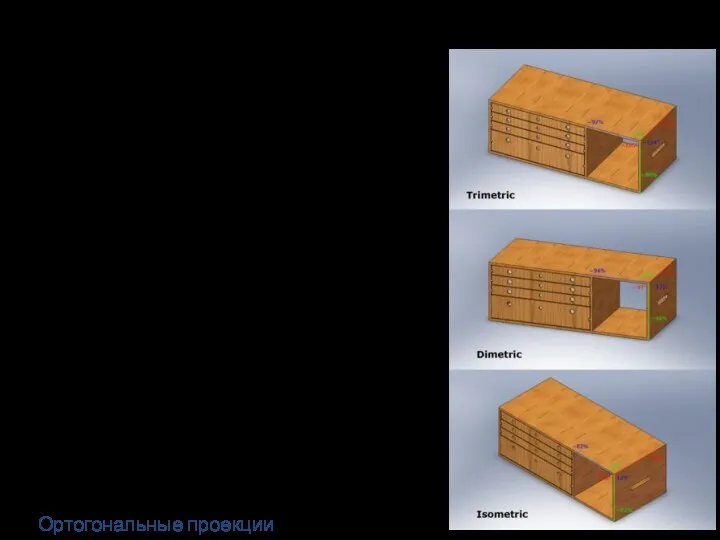
- 20. Если коэф. искажения по всем трём осям не равны p≠q≠r, то проекция называется триметрической. Если коэф.
- 21. p≠q ≠ r , триметрическая проекция p=r, q=1/2p, диметрическая проекция p=q=r , изометрическая проекция Ортогональные проекции
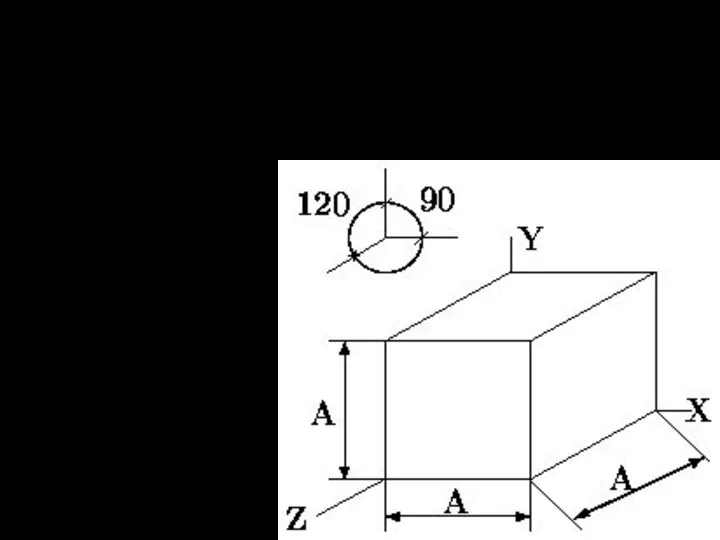
- 22. Изометрическая прямоугольная проекция Наиболее распространенный случай аксонометрических проекций. Нормаль плоскости проекции образует равные углы с каждой
- 23. Коэффициенты искажения: По теореме синусов: sin2 α +sin2 β +sin2 γ =1 sin2 α =1-cos2 α
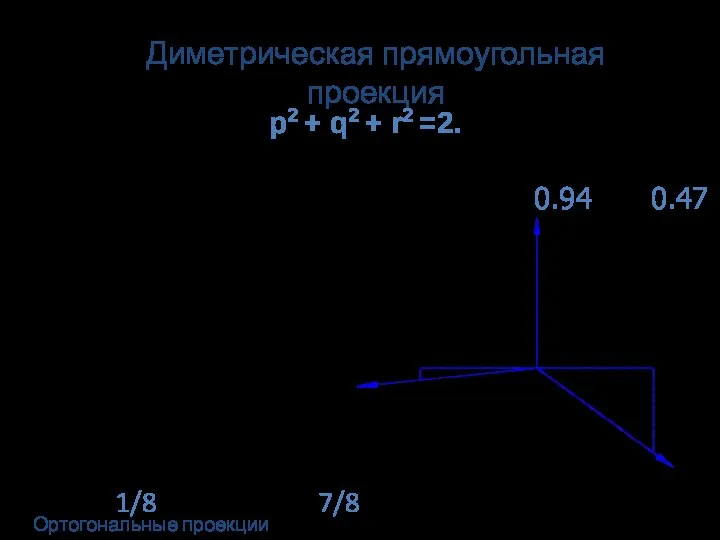
- 24. p2+q2+r2=2 – для прямоугольной аксонометрии сумма квадратов коэффициентов искажения = 2. Установим численные значения коэффициентов искажения
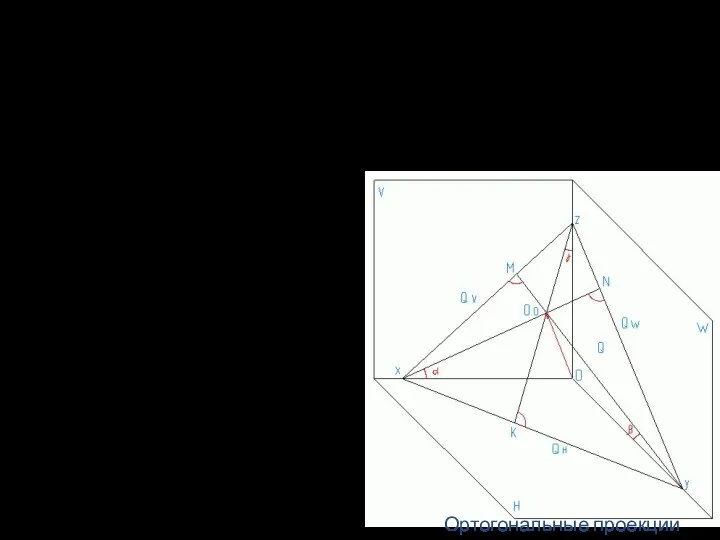
- 25. Треугольник следов – равносторонний. Угол между высотами в равностороннем треугольнике = 120°. Ось z располагается вертикально.
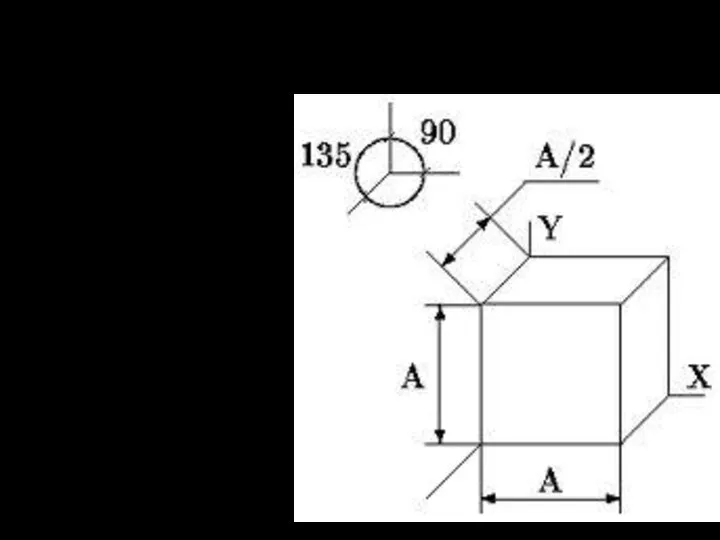
- 26. Треугольник следов – равнобедренный. Приближённо аксонометрические оси диметрической проекции можно построить, если принять tg 7°10'=1/8, а
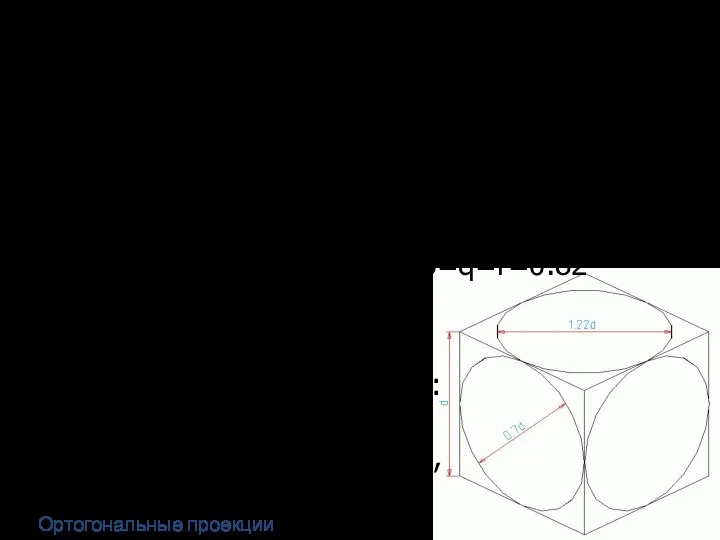
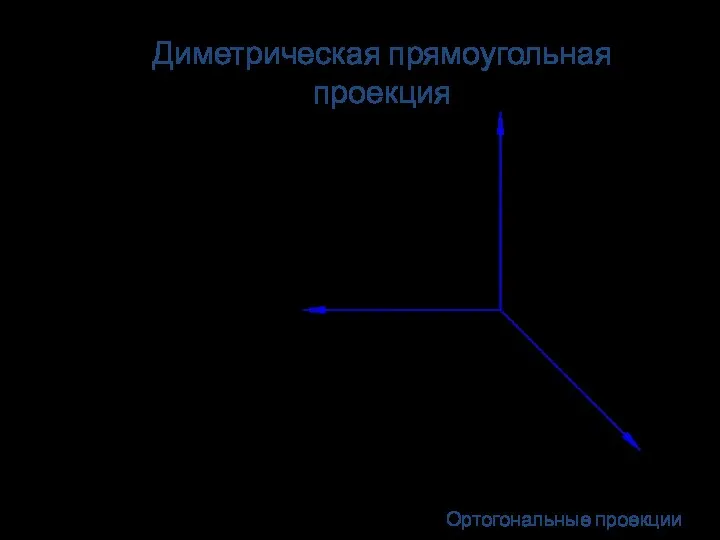
- 27. На практике используют приведённые коэффициенты искажения p=r=1; q=0,5. Тогда получается проекция, увеличенная в 1,06 раза. Диметрическая
- 28. Косоугольные проекции Нормаль плоскости параллельна оси X Лучи составляют с плоскостью проекции угол до 90°.
- 29. Косоугольные проекции Нормаль плоскости проекции не совпадает с направлением проецирующих лучей. Плоскость проекции перпендикулярна одной из
- 30. Косоугольная фронтальная диметрия (Cabinet) p = r = 1.0; q = 0.5; β = γ =135
- 31. Косоугольная горизонтальная изометрия (Cavalier) p = r = q = 1.0; = γ =120 ; α
- 32. Проекции в однородных координатах
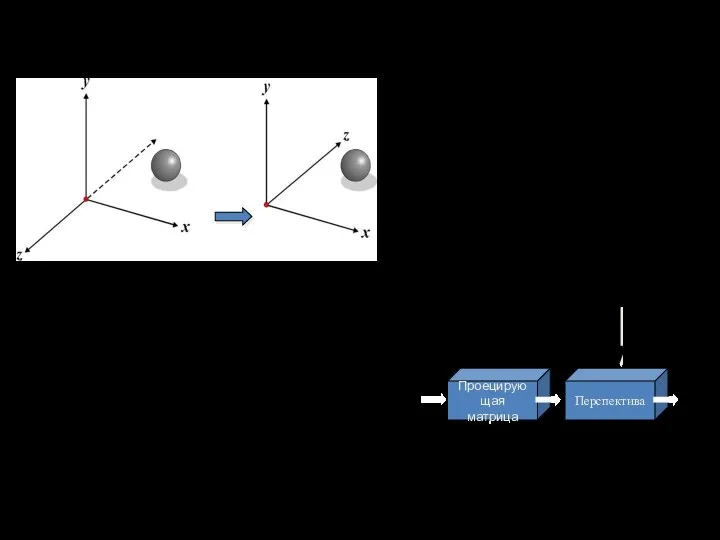
- 33. Аксонометрические проекции могут реализовываться с помощью 2-х поворотов объекта и ортогонального проецирования (переноса) на плоскость, что
- 34. Аксонометрические проекции
- 35. Единичный вектор OX: [1001], если его повернуть: Единичный вектор OY: [0101], если его повернуть: Координаты вектора
- 36. Для изометрии справедливо p=r=q, 3p2=2. Тогда: Для диметрии справедливо: p=r=2q; 2p2 + p2/4 = 2. Тогда
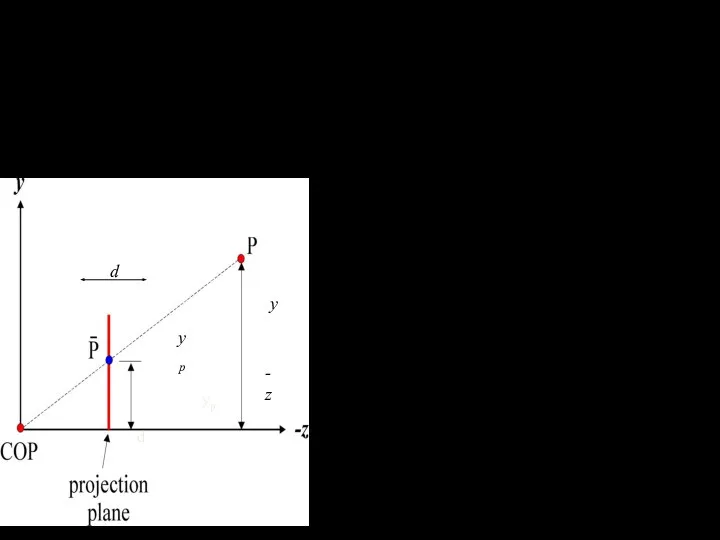
- 37. Точка P=(0,0,1) проецируется в точку P’. Плоскость проекции совпадает с XOY. Направление проецирования задаётся: (Lcosα, Lsinα,-1),L=1/tan(β);
- 38. Матрица косоугольной проекции для случая проецирования в плоскость Z = 0, выполняет: плоскости с заданной координатой
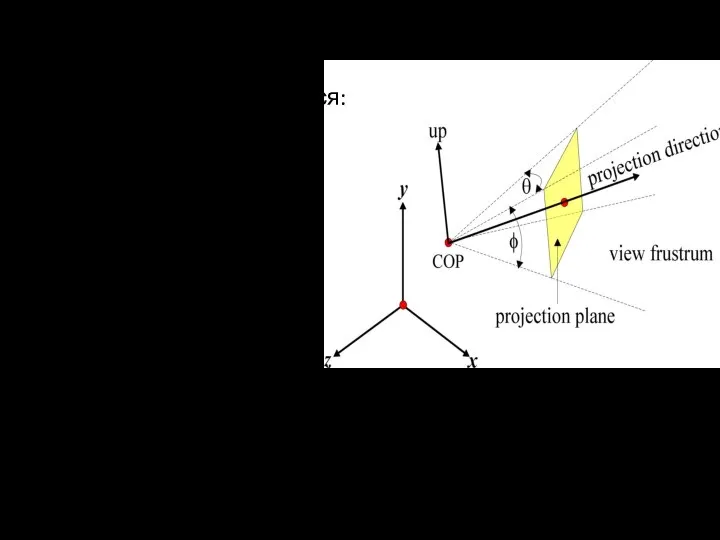
- 39. Более сложные! Для построения учитываются: ракурс; перспективы; объём видимости (в виде усечённой пирамиды) или угол обзора
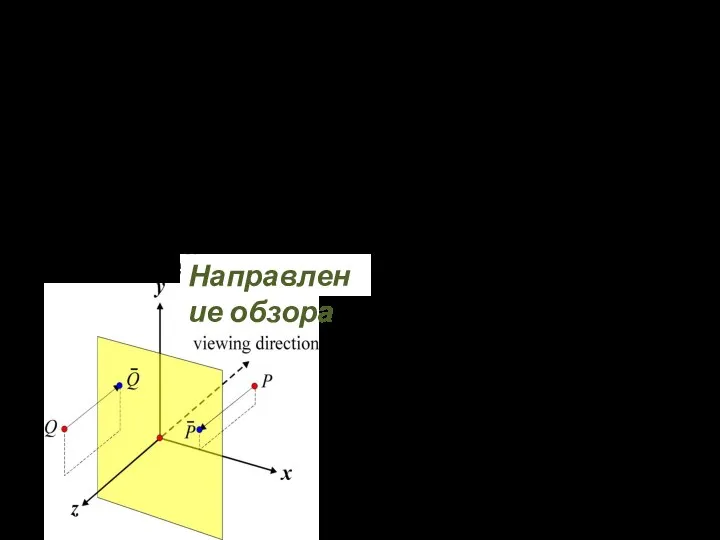
- 40. Если поместить центр проекции в центр координат и направление взгляда ориентировать по положительному направлению оси –z,
- 41. Отражение оси z для перехода в левую систему координат ⇒ увеличение z подразумевает увеличение расстояния до
- 42. В зависимости от приложений могут использоваться различные механизмы для задания перспективных искажений: углы обзора (field of
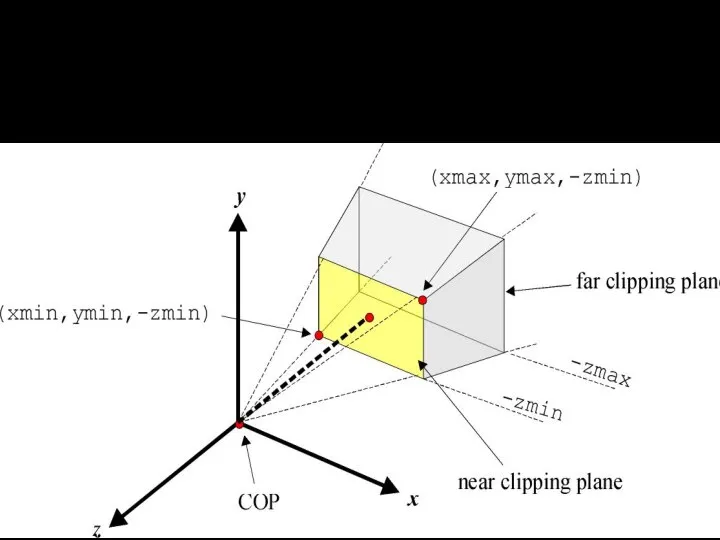
- 43. glFrustrum(xmin, xmax, ymin, ymax, zmin, zmax); Центральные проекции
- 44. glFrustrum Все точки на линии задаваемой COP и координатами(xmin,ymin,-zmin)будут спроецированы в нижнюю левую точку устройства вывода.
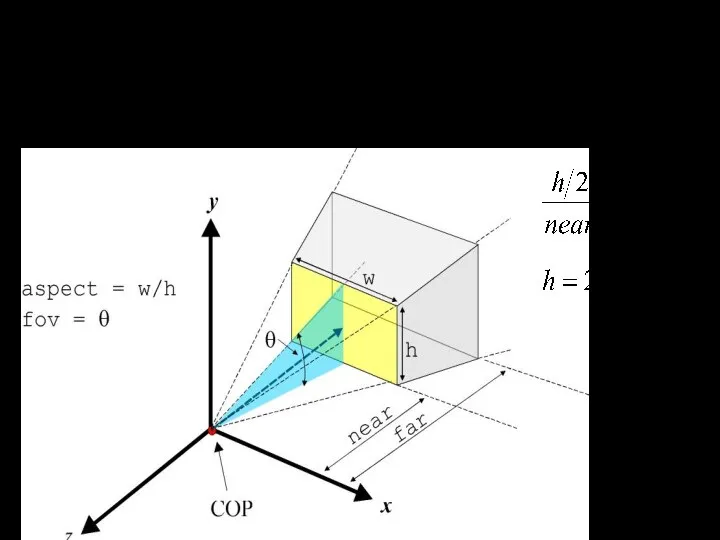
- 45. gluPerspective(fov, aspect, near, far); Центральные проекции
- 46. gluPerspective Предназначение функции упростить определение перспективных проекций. Позволяет создавать симметричные раструбы камеры (symmetric frustrums). Точка наблюдения
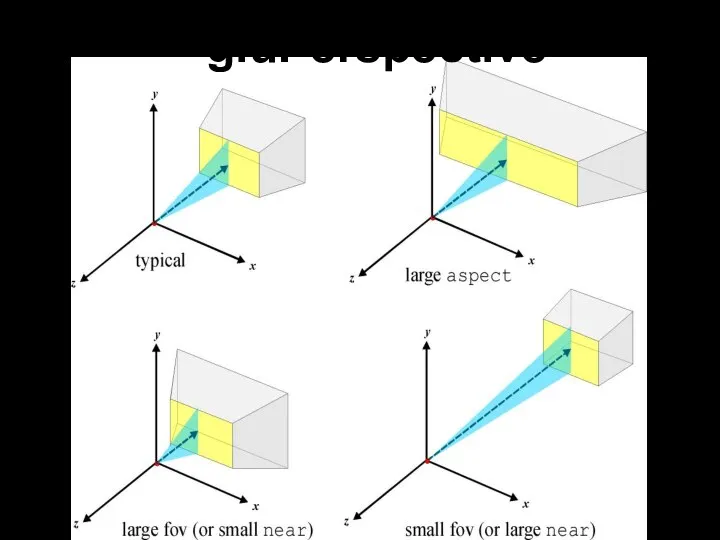
- 47. gluPerspective
- 49. Скачать презентацию

















![Единичный вектор OX: [1001], если его повернуть: Единичный вектор OY: [0101], если](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1120854/slide-34.jpg)
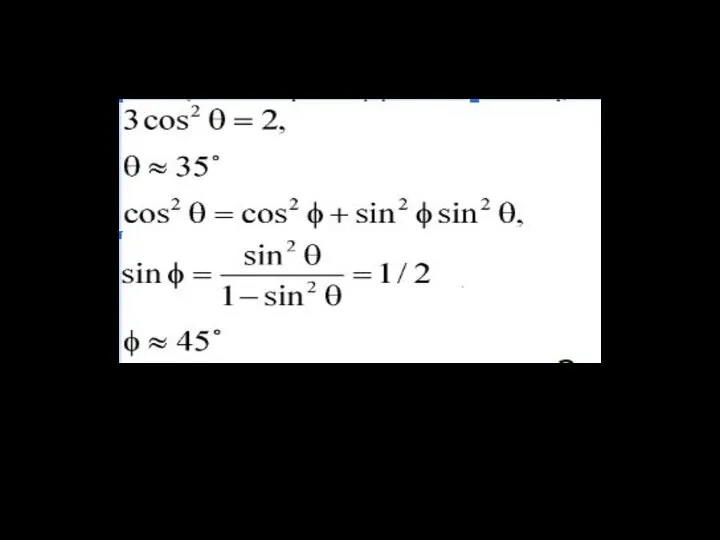





 Теоретико-методологические ориентиры инклюзивного образования
Теоретико-методологические ориентиры инклюзивного образования Судьба свободолюбивой личности в романтической поэме М.Ю.Лермонтова «Мцыри»
Судьба свободолюбивой личности в романтической поэме М.Ю.Лермонтова «Мцыри» Tauride Gardens or Tavrichesky Garden
Tauride Gardens or Tavrichesky Garden  Почему Лига Наций не смогла сохранить мир после Первой мировой войны
Почему Лига Наций не смогла сохранить мир после Первой мировой войны Рисуем рыбку
Рисуем рыбку Интеллектуальная электроэнергетика
Интеллектуальная электроэнергетика 222 группа. Лукояновский педагогический колледж им. А.М. Горького
222 группа. Лукояновский педагогический колледж им. А.М. Горького Задачи апробации электронных учебников
Задачи апробации электронных учебников Законодательные возможности участия граждан в управлении природными ресурсами
Законодательные возможности участия граждан в управлении природными ресурсами Шоколад
Шоколад Приемная кампания 2021 в АПОУ УР ГАПТ
Приемная кампания 2021 в АПОУ УР ГАПТ Презентация на тему Цепи питания
Презентация на тему Цепи питания  Неотложная терапия для детей
Неотложная терапия для детей Презентация на тему Средневековый город и его обитатели
Презентация на тему Средневековый город и его обитатели  Презентация на тему Пейзаж и его разновидности
Презентация на тему Пейзаж и его разновидности Круговой метод тренировки
Круговой метод тренировки Об амфибиях и рептилиях, которых многие совсем не любят
Об амфибиях и рептилиях, которых многие совсем не любят Презентация на тему Не с существительными (5 класс)
Презентация на тему Не с существительными (5 класс) Презентация на тему Строчная буква с
Презентация на тему Строчная буква с  Коммуникация как инструмент управления командой
Коммуникация как инструмент управления командой Презентация на тему Эпоха Петра 1
Презентация на тему Эпоха Петра 1 Времена года в творчестве А.С. Пушкина
Времена года в творчестве А.С. Пушкина Неопределённые местоимения
Неопределённые местоимения Модульный курс для аспирантов «Некоторые дискуссионные проблемы в современном страховании» Гомелля Владимир Борисович к.э.н.,
Модульный курс для аспирантов «Некоторые дискуссионные проблемы в современном страховании» Гомелля Владимир Борисович к.э.н.,  Приемы наблюдения за противником и местностью, действиями соседей и за сигналами командира на месте и в движении
Приемы наблюдения за противником и местностью, действиями соседей и за сигналами командира на месте и в движении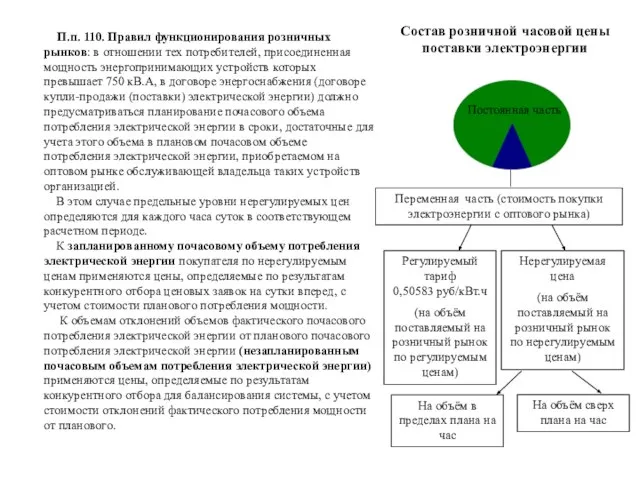 Состав розничной часовой цены поставки электроэнергии
Состав розничной часовой цены поставки электроэнергии Солнечный Сидней
Солнечный Сидней Компьютерная зависимость
Компьютерная зависимость