Медианы, биссектрисы и высоты треугольника. Свойства равнобедренного треугольника

Медианы треугольника
Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны
На рисунке АА₁ , ВВ₁ и СС₁ – медианы.
Свойства медиан
1. Медианы треугольника точкой их пересечения делятся в отношении 2:1 (считая от вершин треугольника).
2. Медиана делит треугольник на два равновеликих треугольника. (Два треугольника равновелики, если их площади равны.)
3. Три медианы треугольника делят треугольник на шесть равновеликих треугольников

Биссектриса треугольника
Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч с началом в вершине угла, делящий угол на два равных угла
На рисунке отрезок EG – это биссектриса угла Е
Свойства биссектрис
Три биссектрисы треугольника пересекаются в одной точке
2. Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам.

Высоты треугольника
Высота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
В остроугольном треугольнике все три высоты лежат внутри треугольника.
В тупоугольном треугольнике две высоты пересекают продолжение сторон и лежат вне треугольника; третья высота пересекает сторону треугольника.

Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Равные стороны называются боковыми, а последняя — основанием.
Свойства равнобедренного треугольника
1 свойство: Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.
2 свойство: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

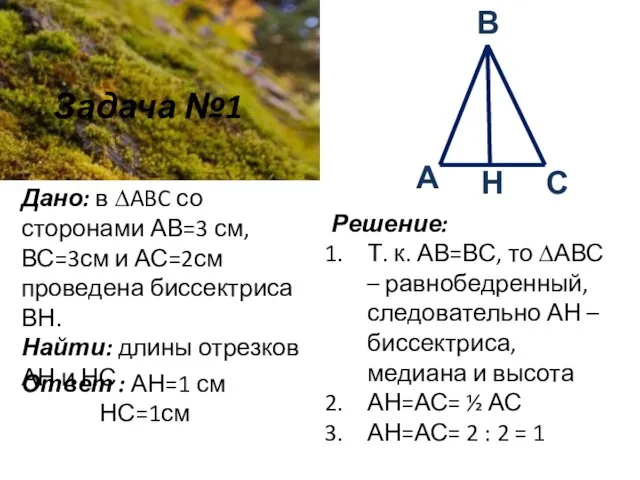
Задача №1
Дано: в ∆ABC со сторонами АВ=3 см, ВС=3см и АС=2см проведена биссектриса ВН.
Найти: длины отрезков АН и НС
Ответ : АН=1 см
НС=1см
Решение:
Т. к. АВ=ВС, то ∆АВС – равнобедренный, следовательно АН – биссектриса, медиана и высота
АН=АС= ½ АС
АН=АС= 2 : 2 = 1

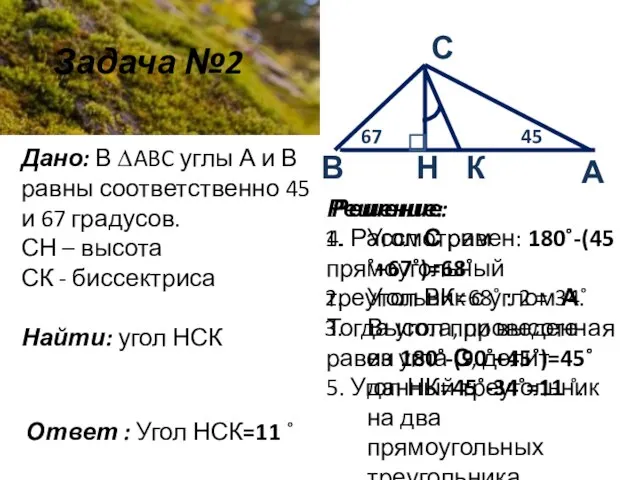
Задача №2
Дано: В ∆ABC углы А и В равны соответственно 45 и 67 градусов.
СН – высота
СК - биссектриса
Найти: угол НСК
Ответ : Угол НСК=11 ˚
А
С
Н
В
Решение:
Угол С равен: 180˚-(45˚+67˚)=68˚
Угол ВК=68˚ : 2 = 34˚
Высота, проведенная из угла С, делит данный треугольник на два прямоугольных треугольника.
К
45
67
Решение:
4. Рассмотрим прямоугольный треугольник с углом А. Тогда угол при высоте равен 180˚-(90˚+45˚)=45˚
5. Угол НК=45˚-34˚=11 ˚.