Содержание
- 2. Ме́тод Мо́нте-Ка́рло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа
- 3. Основными недостатками аналитических методов являются: Недостаточная универсальность основных способов решения. Например, способ разложения в ряд по
- 4. Упрощенно схему алгоритма можно представить в виде:
- 6. Сущность метода Монте-Карло состоит в следующем: требуется найти значение А некоторой изучаемой величины. Для этого выбирают
- 7. Примеры задач, решаемых методом Монте-Карло расчет системы массового обслуживания; расчет качества и надежности изделий; теория передачи
- 8. Простейший пример использования метода Монте-Карло N точек внутри квадрата M точек попало внутрь фигуры Площадь фигуры
- 10. Скачать презентацию
Слайд 2Ме́тод Мо́нте-Ка́рло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении
Ме́тод Мо́нте-Ка́рло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении

большого числа реализаций стохастического (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического(случайного) процесса, который формируется таким образом, чтобы его вероятностные (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического(случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического(случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического(случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии, математики (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического(случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии, математики, экономики (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического(случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии, математики, экономики, оптимизации (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического(случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии, математики, экономики, оптимизации, теории управления и др.
Слайд 3Основными недостатками аналитических методов являются:
Недостаточная универсальность основных способов решения. Например, способ разложения
Основными недостатками аналитических методов являются:
Недостаточная универсальность основных способов решения. Например, способ разложения

в ряд по собственным функциям практически не работают для тех дифференциальных уравнений в частных производных, где переменные не разделяются, и так далее.
Крайне ограниченный набор геометрических условий, для которых возможно решение задачи. Даже сочетание простых, но разнотипных поверхностей делает задачу неразрешимой.
Невозможность расчета физического процесса, вероятностное описание которого известно, но выражение в виде уравнения крайне затруднительно.
Классические численные методы исправляют часть этих недостатков, но зато добавляют свои собственные. Они не страшатся сложной геометрии задач, однако:
Они чрезвычайно громоздки. Объем промежуточной информации трудно вместить даже в память современного компьютера.
Оценка погрешности решения представляет намного более трудную процедуру, чем сам процесс решения. Зачастую она просто невозможна.
Крайне ограниченный набор геометрических условий, для которых возможно решение задачи. Даже сочетание простых, но разнотипных поверхностей делает задачу неразрешимой.
Невозможность расчета физического процесса, вероятностное описание которого известно, но выражение в виде уравнения крайне затруднительно.
Классические численные методы исправляют часть этих недостатков, но зато добавляют свои собственные. Они не страшатся сложной геометрии задач, однако:
Они чрезвычайно громоздки. Объем промежуточной информации трудно вместить даже в память современного компьютера.
Оценка погрешности решения представляет намного более трудную процедуру, чем сам процесс решения. Зачастую она просто невозможна.
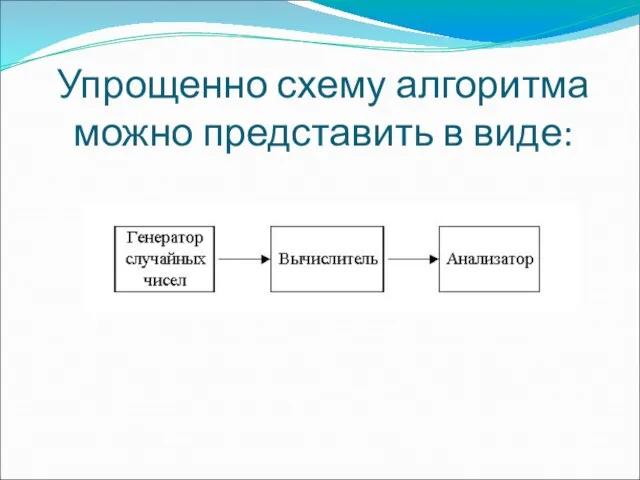
Слайд 4Упрощенно схему алгоритма можно представить в виде:
Упрощенно схему алгоритма можно представить в виде:
Слайд 6Сущность метода Монте-Карло состоит в следующем: требуется найти значение А некоторой изучаемой
Сущность метода Монте-Карло состоит в следующем: требуется найти значение А некоторой изучаемой

величины. Для этого выбирают такую случайную величину X, математическое ожидание которой равно А:
М(Х)=A.
Практически же поступают так: производят N испытаний, в результате которых получают N возможных значений X, вычисляют их среднее арифметическое и принимают его в качестве оценки (приближенного значения) A’ искомого числа A.
Как правило, составляется программа для осуществления одного случайного испытания. Погрешность вычислений, как правило, пропорциональна D/sqrt(N), где D – некоторая постоянная.
Это значит, что N должно быть велико, поэтому метод существенно опирается на возможности ЭВМ. Ясно, что добиться таким путем высокой точности невозможно. Это один из недостатков метода. Во многих задачах удается значительно увеличить точность, выбрав способ расчета, которому соответствует значительно меньшее D.
М(Х)=A.
Практически же поступают так: производят N испытаний, в результате которых получают N возможных значений X, вычисляют их среднее арифметическое и принимают его в качестве оценки (приближенного значения) A’ искомого числа A.
Как правило, составляется программа для осуществления одного случайного испытания. Погрешность вычислений, как правило, пропорциональна D/sqrt(N), где D – некоторая постоянная.
Это значит, что N должно быть велико, поэтому метод существенно опирается на возможности ЭВМ. Ясно, что добиться таким путем высокой точности невозможно. Это один из недостатков метода. Во многих задачах удается значительно увеличить точность, выбрав способ расчета, которому соответствует значительно меньшее D.
Слайд 7Примеры задач, решаемых методом Монте-Карло
расчет системы массового обслуживания;
расчет качества и надежности изделий;
теория
Примеры задач, решаемых методом Монте-Карло
расчет системы массового обслуживания;
расчет качества и надежности изделий;
теория

передачи сообщений;
вычисление определенного интеграла;
задачи вычислительной математики;
задачи нейтронной физики и другие
вычисление определенного интеграла;
задачи вычислительной математики;
задачи нейтронной физики и другие
Слайд 8Простейший пример использования метода
Монте-Карло
N точек внутри квадрата
M точек попало внутрь фигуры
Площадь
Простейший пример использования метода
Монте-Карло
N точек внутри квадрата
M точек попало внутрь фигуры
Площадь

фигуры равна M/N
- Предыдущая
Решение задач экологического мониторинга Следующая -
Мораль и нравственность 
 Услуги и продукты: данные по Гл. Дорожному управлению
Услуги и продукты: данные по Гл. Дорожному управлению Дыхание растений
Дыхание растений Исследование аудиторий СМИ г. Сыктывкара
Исследование аудиторий СМИ г. Сыктывкара Отсчет до кубка конфедераций
Отсчет до кубка конфедераций Ты - предприниматель2012
Ты - предприниматель2012 Презентация на тему Белый цвет
Презентация на тему Белый цвет Количество студентов ИТ-специальностей в российских вузах и ссузах
Количество студентов ИТ-специальностей в российских вузах и ссузах STARTglobal
STARTglobal Государственно-общественное управление российским образованием
Государственно-общественное управление российским образованием Аналитическая биохимия
Аналитическая биохимия Русско-турецкая война 1877-1878 гг. глазами В.В. Верещагина
Русско-турецкая война 1877-1878 гг. глазами В.В. Верещагина Литература барокко. Драматургия Жана Расина. Творчество Жана де Лафонтена.Творчество Вольтера
Литература барокко. Драматургия Жана Расина. Творчество Жана де Лафонтена.Творчество Вольтера www.ratsp.ru
www.ratsp.ru Меры имущественной поддержки субъектов малого и среднего предпринимательства и самозанятых граждан в городе Кировске
Меры имущественной поддержки субъектов малого и среднего предпринимательства и самозанятых граждан в городе Кировске RT Channel 100 МИЛЛИОНОВ Число просмотров роликов RT на канале YOUTUBE достигло 100 МИЛЛИОНОВ В начале декабря RT стал САМЫМ ПРОСМАТРИВАЕМЫМ КА
RT Channel 100 МИЛЛИОНОВ Число просмотров роликов RT на канале YOUTUBE достигло 100 МИЛЛИОНОВ В начале декабря RT стал САМЫМ ПРОСМАТРИВАЕМЫМ КА ИППП сегодня!
ИППП сегодня! Презентация на тему Драгоценные камни
Презентация на тему Драгоценные камни Презентация на тему Слуховой анализатор Орган равновесия
Презентация на тему Слуховой анализатор Орган равновесия Интерференция света 9 класс
Интерференция света 9 класс Религиозно-рекреационный комплекс Шедруб линг в посёлке Косья
Религиозно-рекреационный комплекс Шедруб линг в посёлке Косья Заимствованные слова 6 класс
Заимствованные слова 6 класс Веселая Ярмарка для для настоящих мужчин и русских красавиц Туристического Комплекса «Ярославна»
Веселая Ярмарка для для настоящих мужчин и русских красавиц Туристического Комплекса «Ярославна» Предпринимательская деятельность граждан. Предпринимательская деятельность
Предпринимательская деятельность граждан. Предпринимательская деятельность Презентация на тему Использование энергии солнца на Земле
Презентация на тему Использование энергии солнца на Земле  Printsipy_organizatsii_sistemy_kontrolya_2022_mai_774_obschee
Printsipy_organizatsii_sistemy_kontrolya_2022_mai_774_obschee Алгоритмы циклическойструктуры, программирование на языке PascalЧасть 2
Алгоритмы циклическойструктуры, программирование на языке PascalЧасть 2 Презентация на тему Прощай, Азбука! 1 класс
Презентация на тему Прощай, Азбука! 1 класс Ланец Екатерина Артуровна Учитель начальных классов . Стаж работы в школе-32 года Закончила Серовское педагогическое училище в 197
Ланец Екатерина Артуровна Учитель начальных классов . Стаж работы в школе-32 года Закончила Серовское педагогическое училище в 197