Метод Ньютона(метод касательных)

Историческая справка
Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном, под именем которого и обрёл свою известность.
Впервые метод был опубликован в трактате Алгебра Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном.
Исаак Ньютон
1643-1727

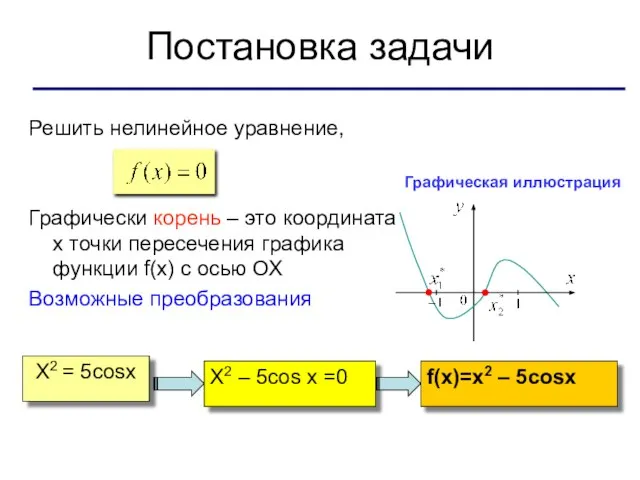
Постановка задачи
Решить нелинейное уравнение,
Графически корень – это координата х точки пересечения графика функции f(x) с осью ОХ
Возможные преобразования
X2 = 5cosx
f(x)=x2 – 5cosx
X2 – 5cos x =0

Исходные данные и результаты
Функция f(x)
Точность вычисления ε>0
Начальное приближение к корню x0
Корень уравнения х*
Количество шагов метода k
Исходные данные
Результаты вычислений

Основная идея метода
Метод Ньютона основан на замене исходной функции f(x), на каждом шаге поиска касательной, проведенной к этой функции. Пересечение касательной с осью Х дает очередное приближение к корню.

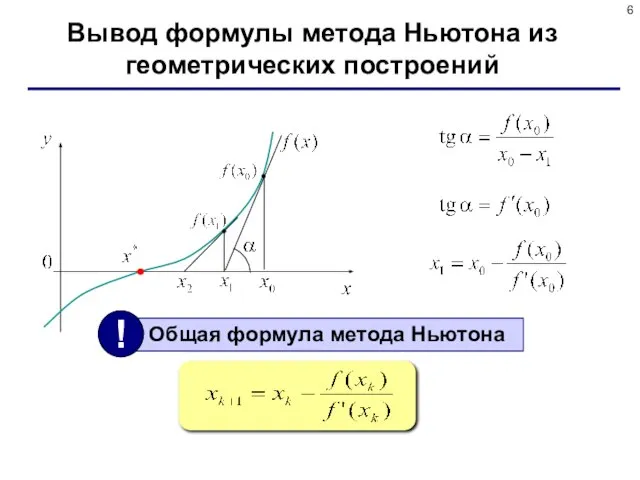
Вывод формулы метода Ньютона из геометрических построений

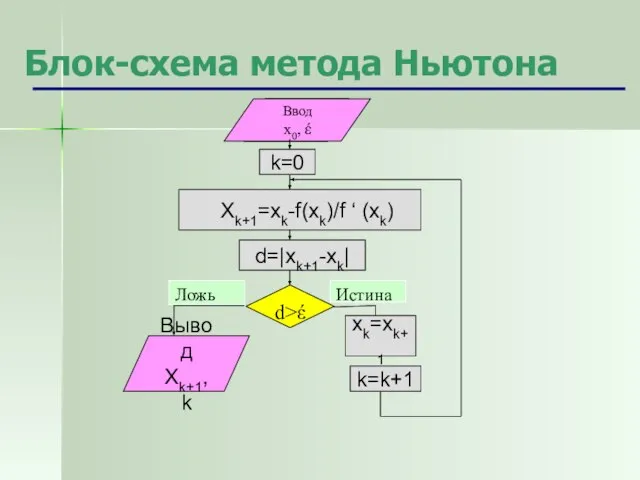
Блок-схема метода Ньютона
Ввод
x0, έ
d>έ
Ложь
Истина
k=0
d=|xk+1-xk|
xk=xk+1
Ввод
x0, έ
Ввод
x0, έ
Вывод
Xk+1, k
k=k+1
Xk+1=xk-f(xk)/f ‘ (xk)

Функция – реализация метода Ньютона
//----------------------------------------------
// Newton решение уравнения методом Ньютона
// Вход: x – начальное приближение
// eps - точность решения
// Выход: решение уравнения f(x)=3x3+2x+5=0
// k - число шагов
//----------------------------------------------
float Newton ( float x, float eps, int &k)
{ float dx, xk;
k = 0;
do {
xk =x - f(x) / df(x);
d = fabs(xk – x);
if ( d > eps )
{ x=xk;
k++;
}
} while (d
return xk;
}
float f ( float x ) {
return 3*x*x*x+2*x+5;
}
float df ( float x ) {
return 9*x*x + 2;
}
Пуск

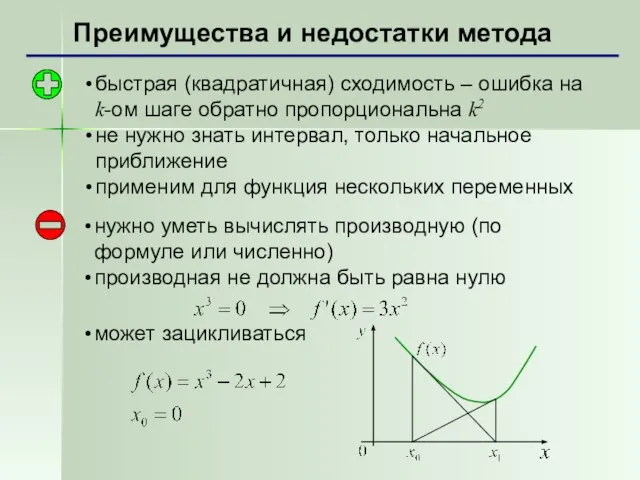
Преимущества и недостатки метода
быстрая (квадратичная) сходимость – ошибка на k-ом шаге обратно пропорциональна k2
не нужно знать интервал, только начальное приближение
применим для функция нескольких переменных
нужно уметь вычислять производную (по формуле или численно)
производная не должна быть равна нулю
может зацикливаться