Метод обратного рассеяния для измерения МДВ. Лекция 10

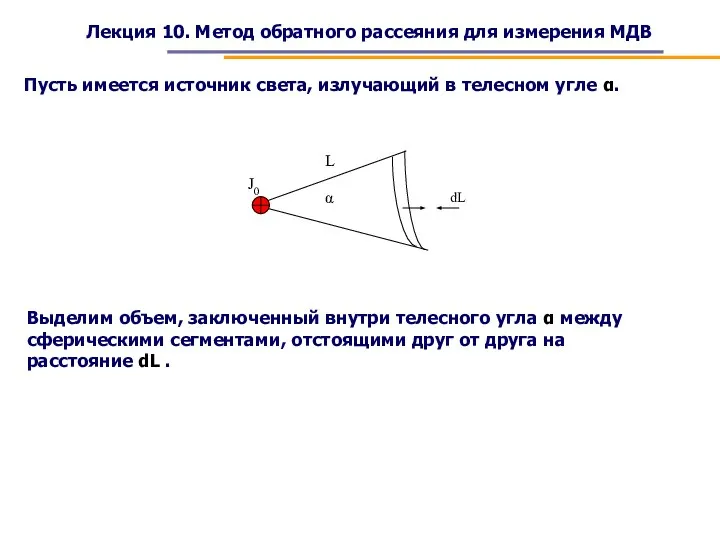
Лекция 10. Метод обратного рассеяния для измерения МДВ
dL
L
J0
α
Пусть имеется источник света, излучающий в телесном угле α.
Выделим объем, заключенный внутри телесного угла α между сферическими сегментами, отстоящими друг от друга на расстояние dL .

Лекция 10. Метод обратного рассеяния для измерения МДВ
Площадь сегмента, ограниченного телесным углом α:
Тогда элементарный объем толщиной dL:
Если число частиц в единице объема равно N, то их число в объеме dV:

Лекция 10. Метод обратного рассеяния для измерения МДВ
Пусть все частицы одинаковые, шарообразные с радиусом r. Тогда поперечник одной частицы:
Излучение, падающее на одну частицу, рассчитаем по закону Буге-Ламберта:

Лекция 10. Метод обратного рассеяния для измерения МДВ
С учетом того, что все излучение распространяется внутри телесного угла α, излучение, падающее на одну частицу:
А излучение, рассеянное одной частицей:

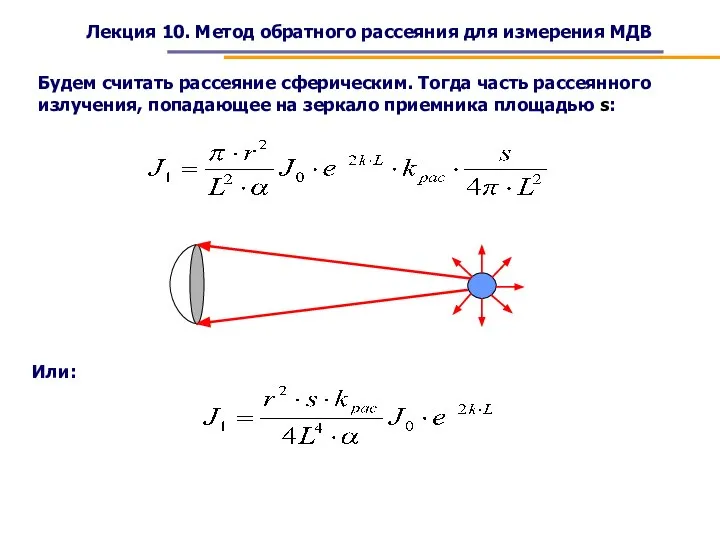
Лекция 10. Метод обратного рассеяния для измерения МДВ
Будем считать рассеяние сферическим. Тогда часть рассеянного излучения, попадающее на зеркало приемника площадью s:
Или:

Лекция 10. Метод обратного рассеяния для измерения МДВ
Излучение, полученное от всех частиц в объеме dV:
Интегральное излучение, полученное от всех частиц на всем протяжении луча:
Или:

Лекция 10. Метод обратного рассеяния для измерения МДВ
Обозначим:
Тогда:
Исследуя зависимость В(L) можно заключить, что при L > 50 м интеграл В не изменятся. Тогда верхний предел в формуле для В можно принять равным 50 м.
Некорректно брать нижний предел интеграл В равным нулю. С учетом того, что источник света находится внутри прибора на некотором расстоянии от стенки, примем нижний предел равным 0,5 м.
Интеграл В в конечном виде не берется. Его можно взять только численно.

Лекция 10. Метод обратного рассеяния для измерения МДВ
Теперь свяжем величину обратного сигнала J с МДВ. По формуле Траберта:
.
Тогда:
Подставив в формулу для J, получим:

Лекция 10. Метод обратного рассеяния для измерения МДВ
С другой стороны, по формуле Кошмидера, приняв ε = 0,03 , имеем:
Значит, интеграл В также зависит от МДВ.
Видно, что МДВ не может быть выражено через J в конечном виде. Обратная задача решена быть не может.
Можно, однако, решить прямую задачу – выразить J через МДВ.
Эту задачу можно решить только численно.

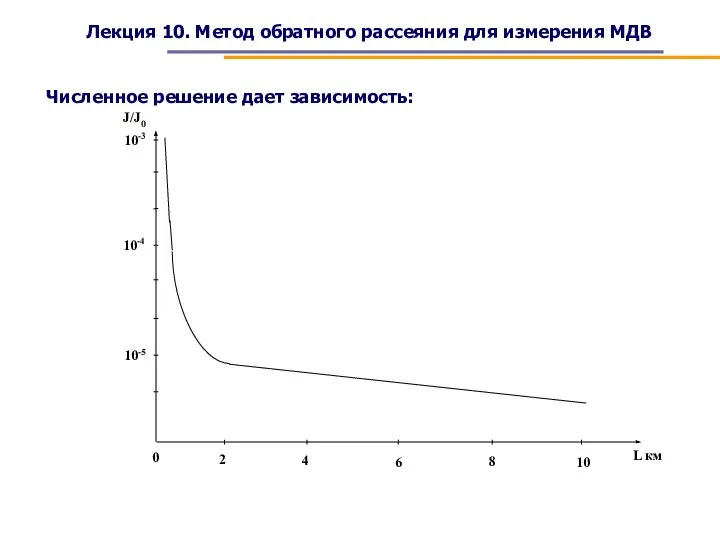
Лекция 10. Метод обратного рассеяния для измерения МДВ
Численное решение дает зависимость: