Содержание
- 2. Тригонометрическая подстановка используется в тех случаях, когда область определения исходного уравнения совпадает с областью значения тригонометрической
- 3. Если из условия задачи следует, что допустимые значения переменной определяются неравенством |x|≤1, то удобны замены x=cos
- 4. Непрерывная функция y=cos x убывает на промежутке [0;π], поэтому также каждое свое значение принимает ровно в
- 5. В случаях, когда переменная может принимать любые действительные значения, используются замены x=tg α, α∈(−π/2;π/2) или x=ctg
- 6. Когда выражение зависит от двух переменных x и y, целесообразно положить x=r sinα, y=r cos α,
- 7. А числа, сумма квадратов которых равна единице, по модулю не превосходят единицы и их можно рассматривать
- 8. Теперь решим несколько примеров
- 9. Пример 1. Решить уравнение Конечно, данный пример можно разрешить, возведя в квадрат, не забыв про условие.
- 10. Легче сделать так: Пусть x=cos α, α∈[0;π], тогда Решение задач Пример 1 Лишь три корня удовлетворяют
- 11. Решение задач Пример 1
- 12. Пример 2. Решить уравнение Перепишем пример в таком виде: Решение задач Пример 2 Пример 1
- 13. Решение задач Пример 2 С учетом замены уравнение принимает такой вид:
- 14. Решение задач Пример 2 Используем формулу разности синусов:
- 15. Решение задач Пример 2 Учитывая, что α∈[0;π], получаем
- 16. Пример 3. Решить уравнение Поделим все члены уравнения на 2. Уравнение примет вид Решение задач Пример
- 17. Докажем, что все корни данного уравнения по модулю не превосходят единицы. Пусть |x|>1, тогда |4x2−3|>1, |x(4x2−
- 18. Положим x=cos α, α∈[0;π]. Уравнение примет вид Решение задач Пример 3
- 19. Условию α∈[0;π] удовлетворяют три значения Решение задач Пример 3
- 20. Поскольку кубическое уравнение не может иметь больше трех различных корней, то мы нашли все решения. Решение
- 21. Пример 4. Решить уравнение Пусть x=t+1, тогда уравнение перепишется в виде Решение задач Пример 4 Введем
- 22. Это уравнение мы уже решали. Его корни Решение задач Пример 4 Два последних значения меньше нуля,
- 23. Перейдем к переменной t, а затем к переменной x Решение задач Пример 4
- 24. Пример 5. При каких а неравенство имеет решение. x=y=0 не является решением неравенства, поэтому поделим обе
- 25. Положим x=r cos α, y=r sin α, α∈[0;π], тогда Решение задач Пример 5
- 26. Оценим выражение Решение задач Пример 5 Наименьшее значение выражения равно −4,5. Значит, при a>−4,5 неравенство имеет
- 28. Скачать презентацию


![Непрерывная функция y=cos x убывает на промежутке [0;π], поэтому также каждое свое](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464601/slide-3.jpg)





![Легче сделать так: Пусть x=cos α, α∈[0;π], тогда Решение задач Пример 1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464601/slide-9.jpg)




![Решение задач Пример 2 Учитывая, что α∈[0;π], получаем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464601/slide-14.jpg)


![Положим x=cos α, α∈[0;π]. Уравнение примет вид Решение задач Пример 3](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464601/slide-17.jpg)
![Условию α∈[0;π] удовлетворяют три значения Решение задач Пример 3](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464601/slide-18.jpg)





![Положим x=r cos α, y=r sin α, α∈[0;π], тогда Решение задач Пример 5](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/464601/slide-24.jpg)

 Учебно-методический семинар «Проблемы перехода на федеральные государственные образовательные стандарты (ФГОС)третьего поколе
Учебно-методический семинар «Проблемы перехода на федеральные государственные образовательные стандарты (ФГОС)третьего поколе Регенерация
Регенерация Фашизм и тоталитарные режимы
Фашизм и тоталитарные режимы Презентация на тему Европейский Север Факторы формирования района
Презентация на тему Европейский Север Факторы формирования района Сравнение отрезков
Сравнение отрезков Презентация на тему: Построим корабль
Презентация на тему: Построим корабль Содержание воспитания, образования, обучения
Содержание воспитания, образования, обучения Памятники религиозных культур в городе томске
Памятники религиозных культур в городе томске Возрастной макияж
Возрастной макияж  Тюнинг NGINX
Тюнинг NGINX Тест по литературе в 6 классе: Иван Сергеевич Тургенев "Муму"
Тест по литературе в 6 классе: Иван Сергеевич Тургенев "Муму" Зимние игры, направленные на развитие сильной, целенаправленной воздушной струи
Зимние игры, направленные на развитие сильной, целенаправленной воздушной струи Права ребёнка в семье
Права ребёнка в семье Добывающий и очистной модуль железнодорожного комплекса
Добывающий и очистной модуль железнодорожного комплекса Опыт внедрения АИАС «АВЕРС: УПРАВЛЕНИЕ ДОУ»
Опыт внедрения АИАС «АВЕРС: УПРАВЛЕНИЕ ДОУ» Наука и образование
Наука и образование Тема внеклассного мероприятия «12 апреля - День космонавтики»
Тема внеклассного мероприятия «12 апреля - День космонавтики» Философия, её смысл, функции и роль в обществе
Философия, её смысл, функции и роль в обществе Общешкольное мероприятие «Олимпиаде в Сочи быть!»Разработал:Учитель музыки высшей категории Мороз Ирина ВладиславовнаМОУ СОШ
Общешкольное мероприятие «Олимпиаде в Сочи быть!»Разработал:Учитель музыки высшей категории Мороз Ирина ВладиславовнаМОУ СОШ Остров мечты
Остров мечты Trip to UK
Trip to UK Спаситель Петербурга
Спаситель Петербурга БЦ Карма Кагью Якутск
БЦ Карма Кагью Якутск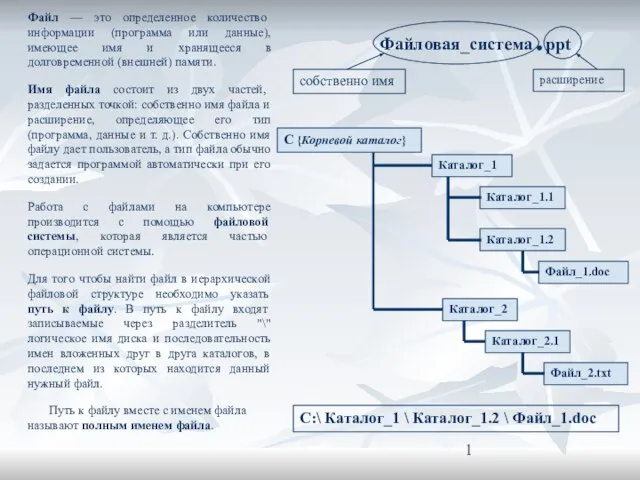 С:\ Каталог_1 \ Каталог_1.2 \ Файл_1.doc
С:\ Каталог_1 \ Каталог_1.2 \ Файл_1.doc Транспозитор спектра, использующего принцип сжатия сигнала во времени для устройств сигнализации об опасности
Транспозитор спектра, использующего принцип сжатия сигнала во времени для устройств сигнализации об опасности Презентация на тему Культура Древней Греции
Презентация на тему Культура Древней Греции Программа кандидата в председатели Студенческого совета МГЛУ
Программа кандидата в председатели Студенческого совета МГЛУ Дружок
Дружок