metod_dekompozicii

ЕГЭ - 2012
62% - не приступали к решению С3
9,1% - получили от 1 до 2 баллов
2,4% - получили 3 балла

Объект исследования
Предмет исследования
Метод декомпозиции
Логарифмические неравенства

Цель исследования
Изучение теоретического обоснования
метода декомпозиции и его применение при решении логарифмических неравенств

Задачи исследования
Изучить и доказать теоремы, которые позволяют заменять сложные выражения на более простые
Рассмотреть примеры применения метода декомпозиции при решении логарифмических неравенств
Сравнить метод интервалов и декомпозиции
На основе полученных результатов сделать выводы
Создать банк заданий, решаемых методом декомпозиции, на сайте гимназии

Гипотеза
При решении логарифмических неравенств
целесообразнее использовать
метод декомпозиции

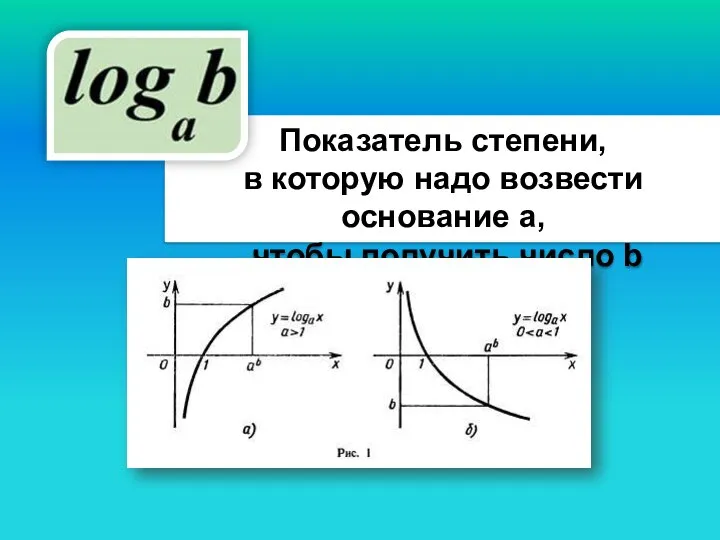
Показатель степени,
в которую надо возвести основание а,
чтобы получить число b

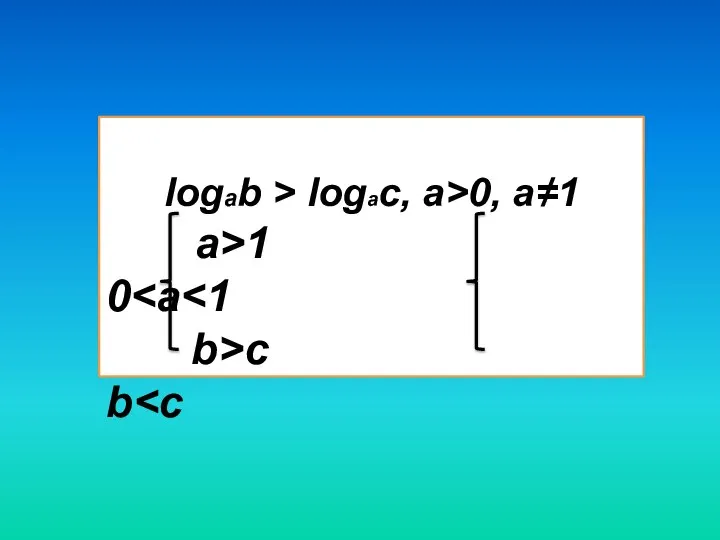
logab > logac, a>0, a≠1
a>1 0
b>c b

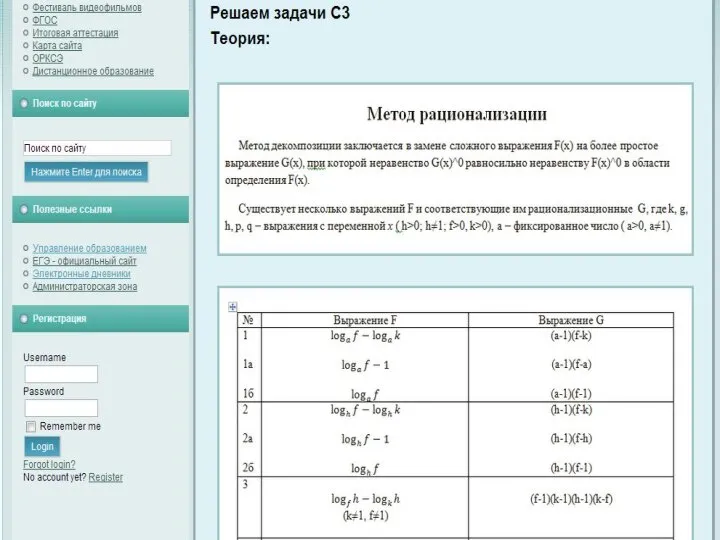
Метод декомпозиции заключается
в замене сложного выражения F(x) на
более простое выражение G(x),
при которой
неравенство G(x)v0 равносильно
неравенству F(x)v0 в
области определения выражения F(x)

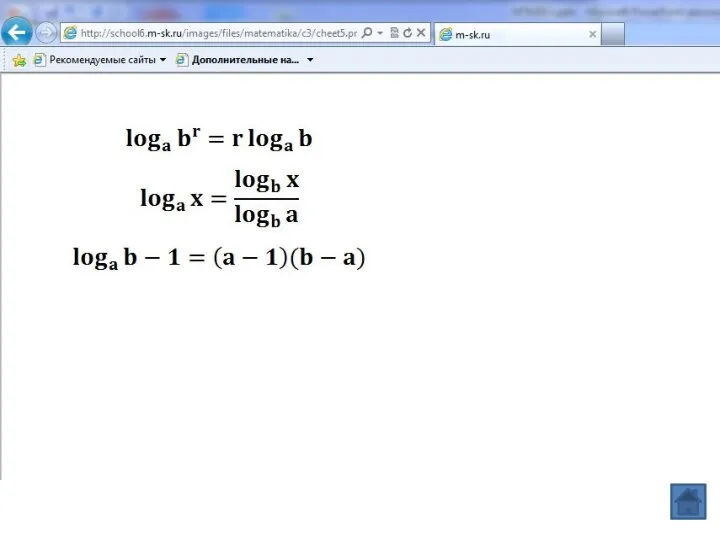
Метод декомпозиции
logab-logac=(a-1)(b-c)
logab-1=(a-1)(b-a)
logab=(a-1)(b-1)
logac-logbc=(c-1)(a-1)(b-1)(b-a)

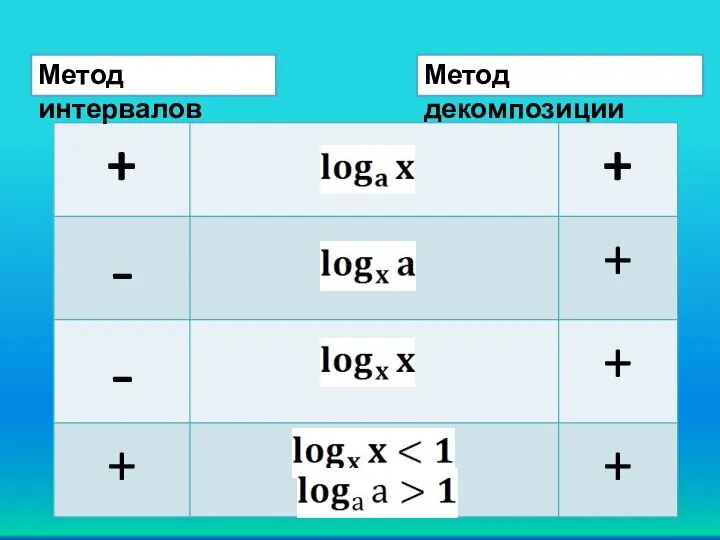
1. Метод интервалов
2. Метод декомпозиции

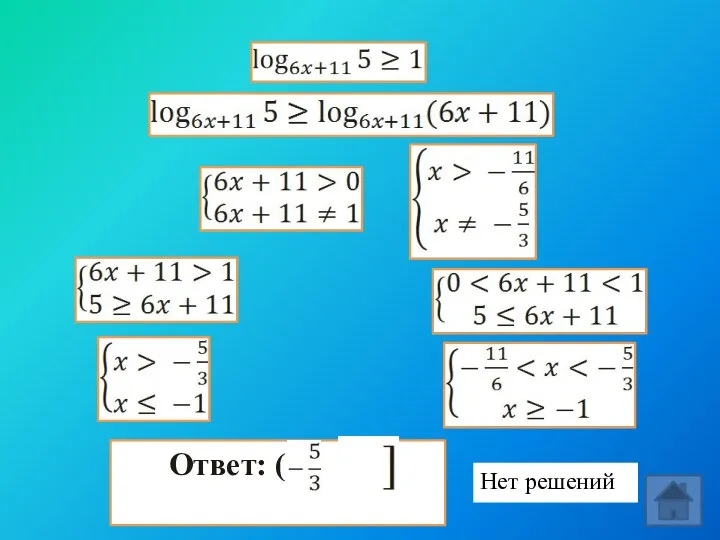
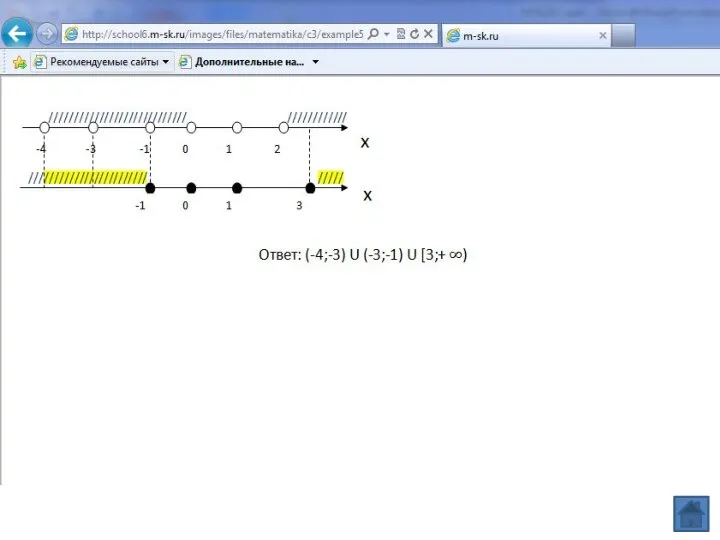
О.Д.З.
a)
b)
Нет решений
Ответ: ( ; -1

Ответ: ( ; -1]

Сравнительная характеристика

Метод декомпозиции
Метод интервалов

Выводы
Метод декомпозиции удобен при решении неравенств с
основаниями, содержащие выражения с переменной
Метод интервалов оптимален для неравенств
c числовым основанием
На решение неравенства методом декомпозиции
затрачивается меньше времени