Методическая разработка

Цель:
оказать помощь учителю в повышении
эффективности преподавания
геометрии на примере обучения
различным способам
доказательства.

Доказательство, его сущность и содержание
Доказательством называется такая логическая
форма мышления, в которой из истинности отдельных суждений с помощью ряда последовательных умозаключений определенным образом выясняется
истинность некоторого положения.
Сущность всякого доказательства состоит в том, что некоторые ранее принятые или доказанные суждения ставятся в соответствие друг другу так,
что их соотношения приводят к другим мыслям, в результате которых получаются новые суждения.

Всякое доказательство включает в себя некоторое доказываемое положение, называемое тезисом.
За основание всякого доказательства принимают некоторые истинные суждения. Эти суждения называются аргументами.
В доказательстве выделяется и третья его часть – демонстрация или способ доказательства.
После того, как в ходе доказательства высказанное предположение подтверждено, тезис становится истинным суждением.

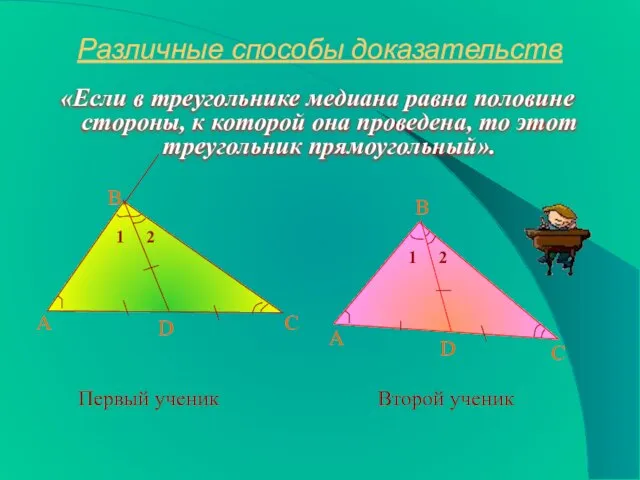
Различные способы доказательств
«Если в треугольнике медиана равна половине стороны, к которой она проведена, то этот треугольник прямоугольный».
D
С
А
В
1
2
2
1
D
С
В
А
Первый ученик
Второй ученик

Первые доказательства и их разновидности
Практику отыскания различных способов доказательств полезно начинать как можно раньше. Уже на первых уроках необходимо демонстрировать учащимся разнообразие путей, которыми можно прийти к умозаключению. Очень важно в это время обучать учащихся тому, как отыскивать различные варианты решений. Большую роль здесь должна играть наглядная иллюстрация способов решения.
«Сравнение отрезков и действия над ними»
.
.
.
.
А
D
С
В
На отрезке АВ взяты точки C и D
так, что АС = BD.
Сосчитать число отрезков и выделить среди них равные пары.

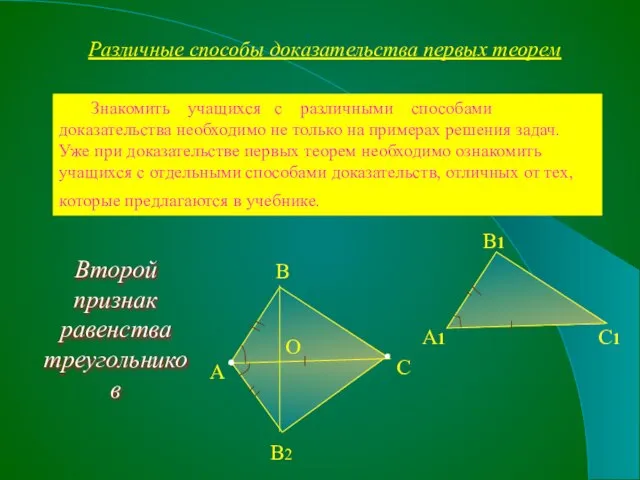
Различные способы доказательства первых теорем
Знакомить учащихся с различными способами доказательства необходимо не только на примерах решения задач. Уже при доказательстве первых теорем необходимо ознакомить учащихся с отдельными способами доказательств, отличных от тех, которые предлагаются в учебнике.
О
В2
С
В
A
С1
В1
A1
.
.
Второй признак
равенства
треугольников

Доказательства, способствующие выработке у учащихся
навыков работы с книгой
Успех учебы во многом зависит от умения учащихся
работать с книгой, в частности с учебником. В связи
с этим одной из важнейших задач обучения является
привитие учащимся навыков этой творческой работы.
А1
С1
В1
А
В2
В
С
Признак равенства
прямоугольного
треугольника
по гипотенузе и катету

Доказательства, способствующие закреплению
изученных положений
Учитель может навести учащихся на путь поиска способов доказательства уже после рассмотрения доказательства учебника. В этом случае предложенное доказательство явится закреплением ранее изученного материала.
D
С
В
А
Против большего угла
в треугольнике
лежит большая сторона

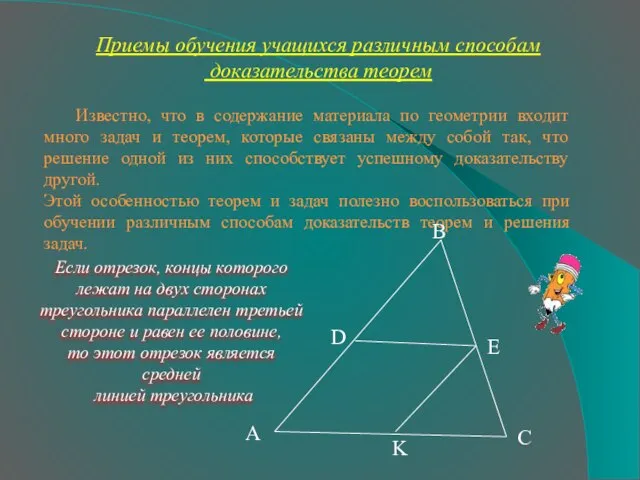
Приемы обучения учащихся различным способам
доказательства теорем
Известно, что в содержание материала по геометрии входит много задач и теорем, которые связаны между собой так, что решение одной из них способствует успешному доказательству другой.
Этой особенностью теорем и задач полезно воспользоваться при обучении различным способам доказательств теорем и решения задач.
D
В
E
С
K
А
Если отрезок, концы которого
лежат на двух сторонах
треугольника параллелен третьей
стороне и равен ее половине,
то этот отрезок является средней
линией треугольника

Итак, если учителю удастся привить детям
интерес к отысканию различных способов
решения задач и разных способов доказательств
теорем, то он может испытать, а, следовательно,
и развить исследовательские способности учащихся.
Заключение