Методические особенности обучения учащихся решению уравнений в курсе математики 5-7 классов

Уравнение – это золотой ключ, открывающий все математические сезамы.
С. Коваль

Цели:
рассмотреть различные виды уравнений, изучаемые в курсе математики 5-7 классов;
привести алгоритмы их решения;
дать методические рекомендации по обучению учащихся решению уравнений.

Алгоритм – понятное предписание, указывающее, какие операции и в какой последовательности необходимо выполнить с данными, чтобы решить любую задачу данного типа.

Характеристические свойства понятия «алгоритм»:
Свойство массовости
Свойство дискретности и элементарности шагов
Свойство результативности
Свойство детерминированности

Всякий алгоритм описывает общий метод решения класса однотипных задач

Правило - «свернутый» алгоритм

Всякий алгоритм можно назвать правилом, но не всякое правило можно назвать алгоритмом

Три основных этапа:
введение алгоритма;
усвоение алгоритма;
применение алгоритма.

Цели этапов:
цель первого этапа – актуализация знаний, необходимых для введения и обоснования алгоритма, а также формулирование алгоритма;
цель второго этапа – отработка операций, входящих в алгоритм, и усвоение их последовательности;
цель третьего этапа – отработка алгоритма в знакомых (при варьировании исходных данных) и незнакомых ситуациях.

Формы работы с учащимися:
на первом этапе - устная работа на повторение.
на втором этапе – письменная коллективная работа с широким использованием комментирования выполняемых действий.
на третьем этапе – самостоятельная работа.

V класс
Уравнения решаются на основе зависимости между результатом и компонентами арифметического действия.

a+x=b
Правило:
«Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое».

a – x = в
x – a = в
1) «Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность»;
2) «Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность».

V класс
13899 + x = 2716 + 13899
4х + 4х = 424
15а – 8а = 714
8,6 – (x + 2,75) = 1,85
45,7х + 0,3х – 2,4 = 89,6
x + 2,8 = 3,72 + 0,38

V класс
1) x + 37 = 85;
2) m – 94 = 18;
3) 85 – z = 36;
4) 4x = 144;
5) x : 8 = 13;
6) 42 : x = 6

V класс
Правило 1: Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Правило 2: Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.
Правило 3: Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Правило 4: Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Правило 5: Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Правило 6: Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Учащиеся V класса сначала должны определить неизвестный компонент действия, а затем найти его, пользуясь одним из вышеперечисленных правил.
x + 25 = 50
x = 50 – 25
x = 25
Ответ: 25
y + 64 = 48 + 38
y + 64 = 86
y = 86 – 64
y = 22
Ответ: 22

Задания:
1. Заполните пропуски в формулировках и определениях.
Уравнением называется ____________, содержащее ____________.
Корнем уравнения называется такое значение ______________, при котором уравнение обращается в _____________ равенство.
Чтобы найти неизвестное уменьшаемое, нужно к _____________ вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно _______________ вычесть _______________.

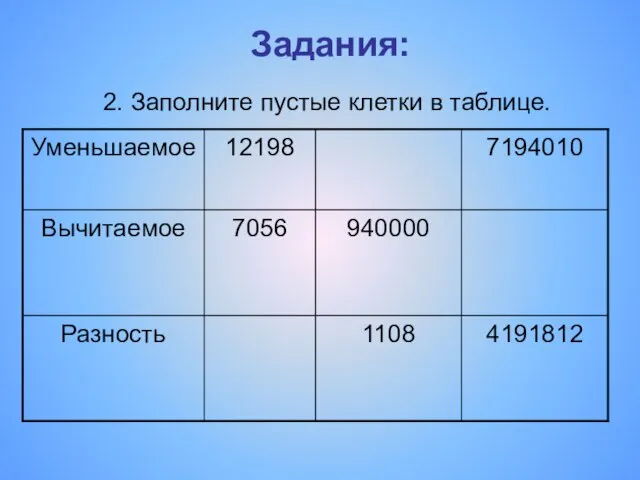
Задания:
2. Заполните пустые клетки в таблице.

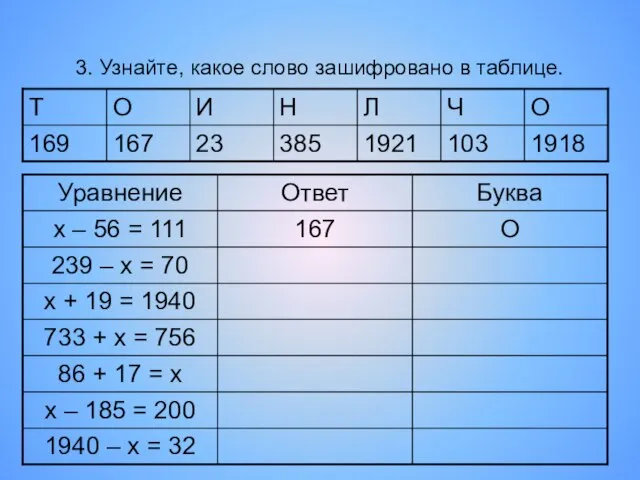
3. Узнайте, какое слово зашифровано в таблице.

VI класс
Общий приём решения уравнений:
слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак.

VI класс
–x = 607
-а = -30,04
-5 + (а - 25) = -4
|y| = 20
|a| = 0
|b| = -3
7,2 – (6,2 - x) = 2,2
|x| = 9

«Универсальный» алгоритм решения линейных уравнений с одним неизвестным вида: 6x – 12 = 5x + 4
1) раскрыть скобки (если таковые имеются);
2) оставить неизвестные в одной части уравнения, известные – в другой (уединение неизвестных);
3) привести подобные слагаемые;
4) разделить обе части уравнения на коэффициент при неизвестном;
5) записать ответ.

Пример
5х + 3 = 2х + 9
5х – 2х = 9 – 3
3х = 6
x = 2
Ответ: 2

Первый этап формирования алгоритма
Устные упражнения на повторение:
1) Перенесите из левой части уравнения в правую то слагаемое, которое не содержит неизвестного:
а) 8х + 5,9 = 7х + 20;
б) 6х – 8 = -5х – 1,6.
2) Оставьте в левой части уравнения все слагаемые, содержащие неизвестное, а в правой – не содержащие неизвестное:
а) 15y – 8 = -6y +4,6;
б) -16z + 1,7 = 2z – 1.

Первый этап формирования алгоритма
Устные упражнения на повторение:
3) Приведите подобные слагаемые:
а) 15t + 8 – 8t – 6;
б) 13a + 4 – 7a - 25a;
в) 24m + 7 – 9m – 14m.
4) Раскройте скобки и приведите подобные слагаемые:
а) 7b – (3b + 1);
б) 3(x - 5) + 10x;
в) -2(x + 1) + x.

Первый вид тестовых заданий
1. Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», _________________ знаки слагаемых, стоящих в скобках.
2. Раскройте скобки:
-17,5 + (3,02 – 2,51) = __________________.
3. -(a + b) = __________________.

Первый вид тестовых заданий
4. Коэффициентом такого выражения, как a или ab, считают _________.
5. Слагаемые, имеющие одинаковую буквенную часть, называют ______________________ слагаемыми.
6. Выполните приведение подобных слагаемых:
b – 2c + 4b – c = _________________________.
7. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то корни уравнения ________________________.

Второй вид тестовых заданий
1. Выражение a + (b + c) можно записать без скобок:
a + (b + c) = a + b + c
2. Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
3. Приведение подобных слагаемых выполняют на основании переместительного свойства умножения.
4. Число -30 является корнем уравнения
0,5х – 15 = х.

Третий вид тестовых заданий
1. Раскройте скобки в выражении: a – (b + c - d)
А) a – b + c – d;
Б) a – b – c + d;
В) a + b + c – d.
2. Найдите значение выражения: 25 – (12 - 53)
А) -40;
Б) -16;
В) 66.
3. Упростите: 5x – 5y – 6x + y
А) –x – 5y;
Б) -6x + y;
В) –x – 4y.
4. Найдите корень уравнения: 4 – 3y = 7 - y
А) 1,5;
Б) -1;
В) -1,5.

Второй этап формирования алгоритма
Решите уравнения:
1) -2x + 16 = 5x – 19
2) 4(3 – 2x) + 24 = 2(3 + 2x)
3) 15 – 3(x - 8) = 3
4) 0,5(4 + x) – 0,4(x - 3) = 2,5
5) 0,4(x - 9) – 0,3(x + 2) = 0,7

Третий этап формирования алгоритма
Решите уравнения:
18 = 3y + 3
6x + 10 = 5x + 15
-5n – 16 = 3n
8 – 5n = 10 – 4n
9m – 8 = 6m + 7

Тестовые задания
1. Решите уравнение: 4,2х + 5 = -7,6
А) 4;
Б) -3;
В) -0,3;
Г) другой ответ.
2. Найдите сумму корней уравнений
х + 11,7 = 8,7 и (3х + 4,6) – 6,6 = 8,7 + 2,2
А) 4,3;
Б) -7,4;
В) 1,3;
Г) другой ответ.

Тестовые задания
3. Отец в два раза старше сына и на 25 лет старше дочери. Сколько лет дочери, если всем вместе им 95 лет?
А) 23;
Б) 24;
В) 48;
Г) другой ответ.

Самостоятельная работа
1. Решите уравнения:
а) 2,1х – 3,5 = 1,4х;
б) 2(4 – 1,9х) = 0,8 – 0,2х.
2. На верхней полке в 3 раза больше книг, чем на нижней. После того, как с верхней полки сняли 15 книг, а на нижнюю добавили 11 книг, книг на обеих полках стало поровну. Сколько книг было на каждой полке первоначально?
3. Путь из города в село турист прошел со скоростью 4,8 км/ч. На обратном пути он увеличил скорость до 6 км/ч, что позволило ему пройти это расстояние на 1 час быстрее. Найдите расстояние от города до села.

VII класс
0,5(4 – 2a) = a – 1,8
2 – a = a – 1,8
a + a = 2 + 1,8
2a = 3,8
a = 1,9
Ответ: 1,9

Алгоритм решения линейного уравнения с двумя переменными типа: 5y – 2x = 1
1) воспользовавшись свойствами уравнений, выразить из данного уравнения одну переменную через другую;
2) воспользовавшись свойствами уравнений, добиться того, чтобы коэффициент при одной из переменных был равен единице;
3) взять произвольное значение одной из переменных и вычислить соответствующее ему значение другой переменной;
4) записать решение исходного (данного) уравнения в виде пары (пар) чисел.

Пример
3x + 2y = 12 (1)
2y = 12 – 3x
y = 6 – 1,5x (2)
если x = 2, то = 6 – 3 = 3;
если x = 6, то = 6 – 9 = -3.
Пары чисел (2; 3), (6;-3) – решение уравнения (1).
уравнение (1) имеет бесконечно много решений

Тестовые задания по теме:
«Уравнение с одной переменной»
1. Выберите уравнения, для которых число -3 является корнем:
1) (2x + 3)(2x - 6) = 0; 3) (2x + 6)(x - 4) = 0;
2) (x2 - 9) + (x2 - 7) = 2; 4) (x + 3)(x2 – 3x + 9) = 0.
а) 1; 2; б) всех; в) 3; 4; г) 2; 3; 4.
2. Найдите все натуральные значения p, при которых корнем уравнения px = 8 является целое число.
а) 1; 2; 4; 8; б) 1; 8; в) 2; 4; г) 2; 4; 8.

Тестовые задания по теме
«Уравнения с двумя переменными»
1. При каком значении c пара (c;3) является решением уравнения
3x – 4y = 6?
а) -6; б) 6.
2. Точка с абсциссой -3 принадлежит графику уравнения x – 2y = 10. Найдите ординату этой точки.
а) -6,5; б) 6,5; в) 4; г) -4.

Самостоятельная работа
1. Решите уравнения:
а) -8х = -24;
б) 50х = -5;
в) -18х = 1.
2. Определите значение x, при котором значение выражения -3х равно:
а) 0; б) 6; в) -12;
3. При каких значениях a уравнение ax = 8:
1) имеет корень, равный -4, 0;
2) не имеет корней;
3) имеет отрицательный корень?