Содержание
- 2. Задача №4 районной олимпиады по информатике Сумма двух чисел. Заданы три числа a, b, c. Необходимо
- 3. Решение задачи Текст программы (мой алгоритм) Решение задачи (мой алгоритм) Ссылки не работают. Для получения текста
- 4. Комбинаторные алгоритмы
- 5. Из предисловия к главе 2 книги С.М. Окулова «Программирование в алгоритмах» Одной из главных целей изучения
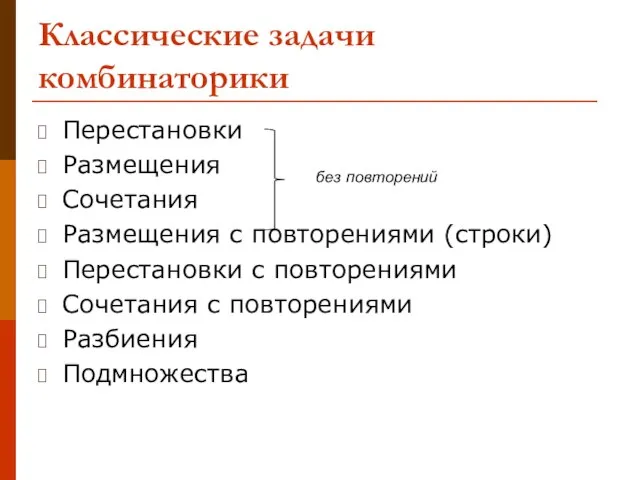
- 6. Классические задачи комбинаторики Перестановки Размещения Сочетания Размещения с повторениями (строки) Перестановки с повторениями Сочетания с повторениями
- 7. Перестановки Сколькими способами можно переставить N различных предметов, расположенных на N различных местах. Примеры: 1. Сколькими
- 8. Размещения Сколькими способами можно выбрать и разместить по М различным местам М из N различных предметов?
- 9. Сочетания (выборки) Сколькими способами можно выбрать М из N различных предметов? Примеры: 1. Сколькими способами можно
- 10. Перестановки Перестановкой конечного множества называется упорядоченная последовательность всех его элементов, в которой каждый элемент встречается ровно
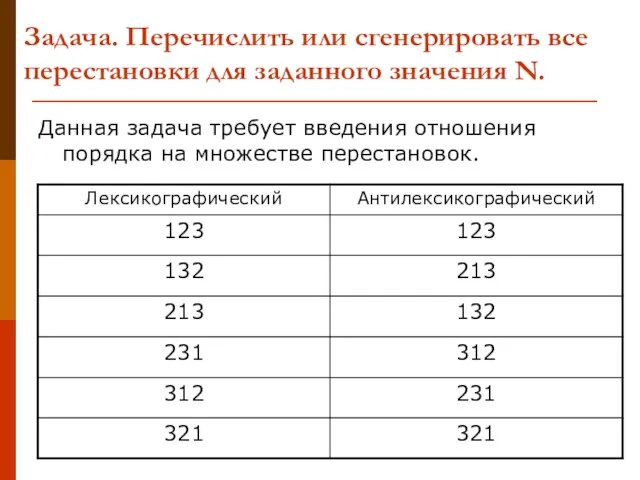
- 11. Задача. Перечислить или сгенерировать все перестановки для заданного значения N. Данная задача требует введения отношения порядка
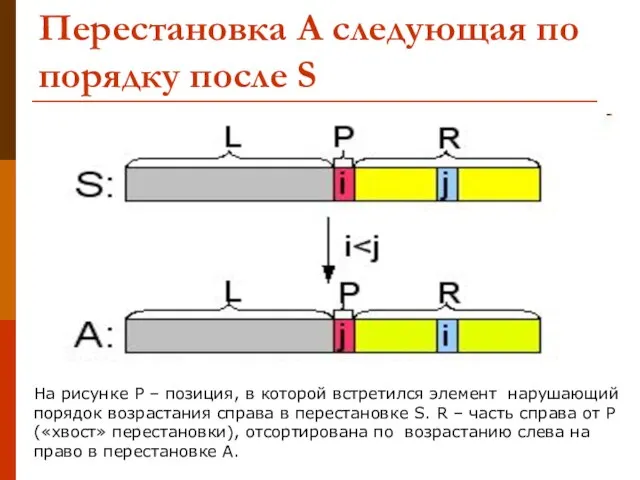
- 12. Перестановка А следующая по порядку после S На рисунке Р – позиция, в которой встретился элемент
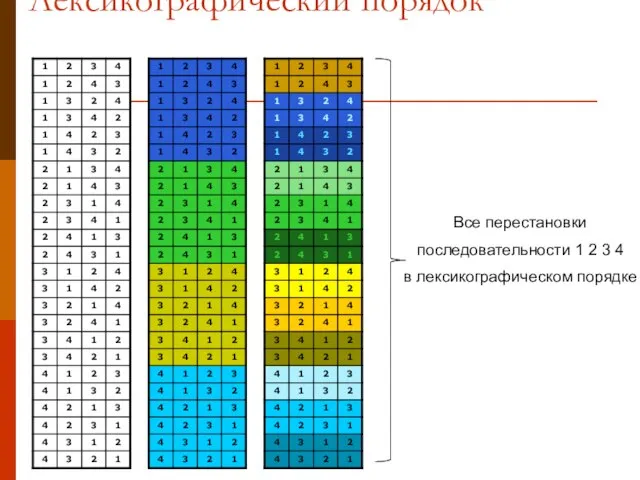
- 13. Лексикографический порядок Все перестановки последовательности 1 2 3 4 в лексикографическом порядке
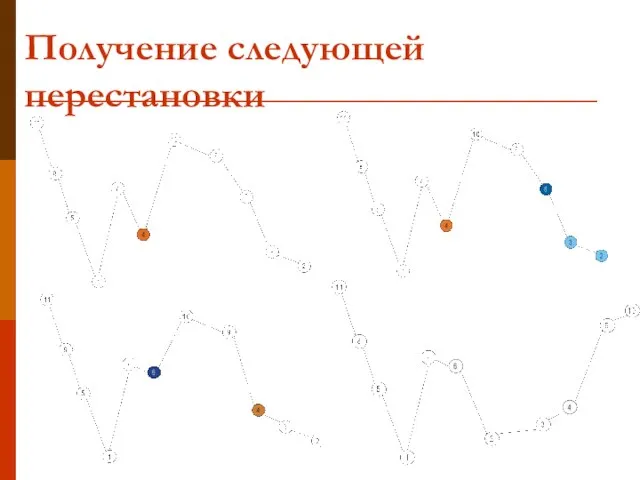
- 14. Получение следующей перестановки
- 15. Получение следующей перестановки 1. Пусть P – массив, содержащий перестановку. 2. Находим первое i с конца
- 16. Решение задачи на основе классического алгоритма генерации перестановок в лексикографическом порядке. Текст программы Решение задачи Ссылки
- 17. Перевод числа а в массив цифр * * * am[0]:=0; while a>0 do begin inc(am[0]); am[am[0]]:=a
- 18. Получение числа, соответствующего полученной перестановке * * * a:=0; for k:=1 to am[0] do a:=10*a+am[p[k]]; *
- 20. Скачать презентацию









![Перевод числа а в массив цифр * * * am[0]:=0; while a>0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/439533/slide-16.jpg)

 Федеральный государственный образовательный стандарт общего начального образования второго поколения
Федеральный государственный образовательный стандарт общего начального образования второго поколения Деструктивные организации
Деструктивные организации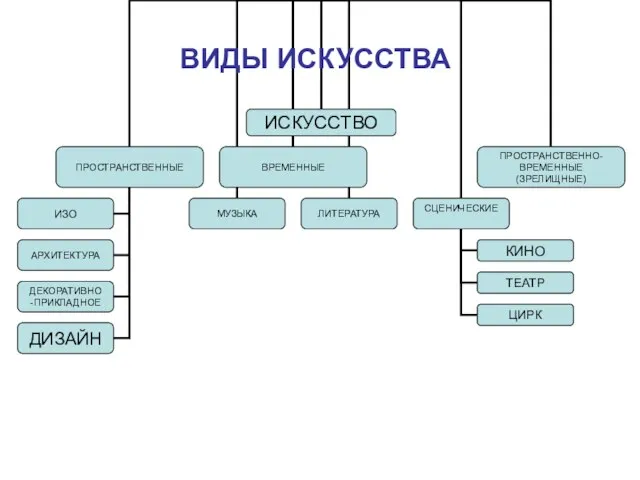 Виды искусства
Виды искусства Психоанализ и культура
Психоанализ и культура Основные законы управления
Основные законы управления Россия в XYIII столетии Россия при Петре I Российская империя как исторический феномен Эпоха дворцовых переворотов Россия при Екат
Россия в XYIII столетии Россия при Петре I Российская империя как исторический феномен Эпоха дворцовых переворотов Россия при Екат План недели Понедельник – Открытие недели начальных классов - День знатоков русского языка Вторник – Всероссийский конкурс по ма
План недели Понедельник – Открытие недели начальных классов - День знатоков русского языка Вторник – Всероссийский конкурс по ма 220 лет РГПУ им. А.И.Герцена
220 лет РГПУ им. А.И.Герцена Презентация на тему Что изучает современная экология?
Презентация на тему Что изучает современная экология?  Экспорт нефти и нормативно-правовое регулирование
Экспорт нефти и нормативно-правовое регулирование Векторная алгебра
Векторная алгебра Физическое развитие детей и подростков (2)
Физическое развитие детей и подростков (2) Презентация на тему Франциск 1
Презентация на тему Франциск 1 Основные виды организационных структур
Основные виды организационных структур Tunti 8. Ruoka
Tunti 8. Ruoka Гражданственность
Гражданственность Особенности региональной работы ЗПИФов недвижимости 27 ноября 2007
Особенности региональной работы ЗПИФов недвижимости 27 ноября 2007 Волейбол
Волейбол Факторы, оказывающие влияние на стоимость геодезических работ. Определение стоимости инженерно-геодезических изысканий
Факторы, оказывающие влияние на стоимость геодезических работ. Определение стоимости инженерно-геодезических изысканий МОУ СОШ №1 г.Краснознаменска урок МХК в 10 классе «Импрессионизм в живописи»
МОУ СОШ №1 г.Краснознаменска урок МХК в 10 классе «Импрессионизм в живописи» Презентация на тему Школьный референдум
Презентация на тему Школьный референдум Региональная инфраструктура сопровождения инновационных процессов в областной системе образования
Региональная инфраструктура сопровождения инновационных процессов в областной системе образования Русский народный праздник «Святки»
Русский народный праздник «Святки» Госбюджет. Внебюджетные фонды. Тема 6
Госбюджет. Внебюджетные фонды. Тема 6 Повышение эффективности системы поддержки научных исследований в интересах модернизации и инновационного развития оА.А. Фурсе
Повышение эффективности системы поддержки научных исследований в интересах модернизации и инновационного развития оА.А. Фурсе Доказательство теоремы Пифагора,основанного на теории подобия
Доказательство теоремы Пифагора,основанного на теории подобия Японская мифология
Японская мифология Научно-практическая конференция«Система взаимоотношений в теплоснабжении.Требования существующего и нового законодательства»
Научно-практическая конференция«Система взаимоотношений в теплоснабжении.Требования существующего и нового законодательства»