Методы поиска в структурированных файлах функции ранжирования

Содержание
Векторная модель
TF-IDF
Косинусная мера
Структурированный файл
на примере XML
Лексические поддеревья
Структурные термы
Расширение векторной модели на случай структурированных файлов
Схожесть контекстов
Okapi BM25
BM25F
BM25Е

Векторная модель
Векторная модель (англ. vector space model) — представление коллекции документов векторами из одного общего для всей коллекции векторного пространства.
Коллекция - неупорядоченное множество документов.
Документ - неупорядоченное множество термов.
Термы (словарные термы) - слова, из которых состоит текст (определение терма зависит от приложения)
В векторной модели термы – это измерения.
Вес терма – координата в данном измерении.

Векторная модель
Более формально
dj = (w1j, w2j, …, wnj), где
dj — векторное представление j-го документа,
wij — вес i-го терма в j-м документе,
n — общее количество различных термов во всех документах коллекции.
Запросы представляются в той же форме, что и документы. Т.е.
q = (w1q,w2q,...,wtq), где
q – векторное представление запроса,
wiq - вес i-го терма в запросе

TF-IDF
TF-IDF (от англ. TF — term frequency, IDF — inverse document frequency) — статистическая мера, используемая для оценки важности слова в контексте документа, являющегося частью коллекции документов. TF-IDF = TF*IDF
ni - число вхождений терма в документ
k – общее число термов в документе
|D| — количество документов в коллекции
— количество документов, в которых встречается терм ti (когда ni≠0)

Косинусная мера

Косинусная мера
ρ(Q,D) – соответствие запроса Q документу D
ti – терм (измерение)
wQ(ti) – вес терма ti в запросе Q
wD(ti) – вес терма ti в документе D

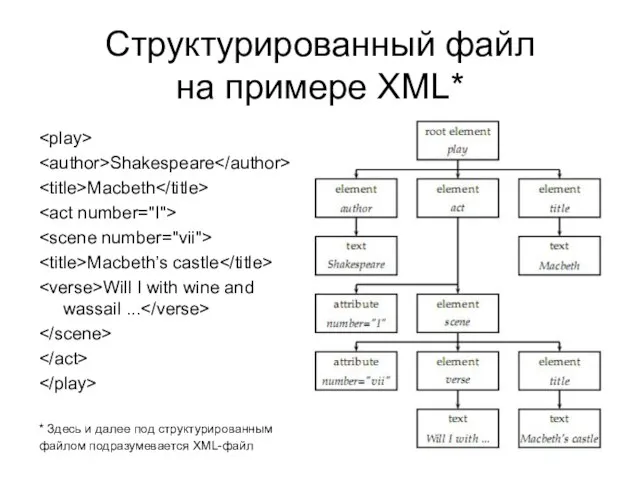
Структурированный файл
на примере XML*
Shakespeare
Macbeth
Macbeth’s castle
Will I with wine and wassail ...
* Здесь и далее под структурированным
файлом подразумевается XML-файл

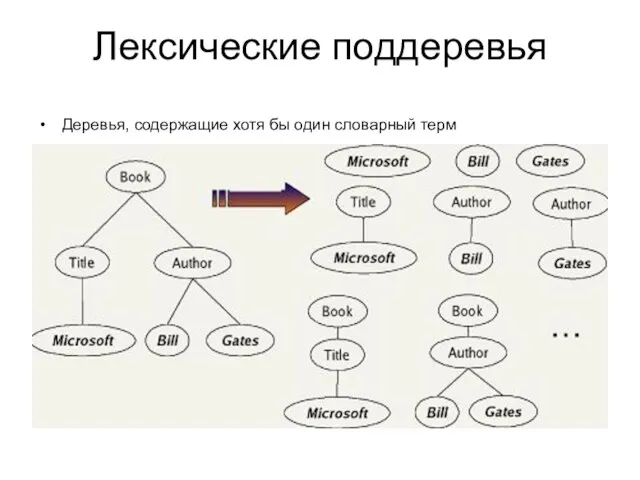
Лексические поддеревья
Деревья, содержащие хотя бы один словарный терм

Лексические поддеревья
С увеличением количества узлов в дереве
растет число лексических поддеревьев.

Структурные термы
Будем рассматривать только такие лексические поддеревья, которые оканчиваются единственным словарным термом
Такие поддеревья называются структурными термами и обозначаются парой (t,c), где t – это терм, c - его XML-контекст.

Расширение векторной модели на случай структурированных файлов
ρ(Q,D) – соответствие запроса Q документу D
(ti,c i) – структурный терм (измерение)
wQ(ti,c i) – вес структурного терма (ti,c i) в запросе Q
wD(ti,c i) – вес структурного терма (ti,c i) в документе D
cr(ci,ck) – схожесть контекстов (context resemblance) ci и ck, 0≤cr(ci,ck) ≤1

Схожесть контекстов
1 способ
|cq| - число узлов в контексте, соответствующем терму из запроса
|cd| - то же, но для документа
если cq соответствует cd
иначе

Схожесть контекстов
2 способ
Рассмотрим запрос в форме
T
Q = q1q2q3 – контекст появления Т в запросе
А = а1а2…а8 – контекст появления Т в произвольном XML документе
Пример:
Q = language/book/title
A = language/media/book/chapter/section/subsection/title/number

Схожесть контекстов
LCS(Q,A)
Longest Common Subsequence
LCS(Q,A) = lcs(Q,A)/|Q|, где
lcs(Q,A) – длина наибольшей общей подпоследовательности Q и А
0 ≤ LCS(Q,A) ≤ 1

Критерии оценки
Контекст А включает больше элементов qi в правильном порядке. (В примере - 3)
Элементы qi появляются ближе к началу А, чем к концу. (В примере – совпадение q1q2q3 с а1а3а7 предпочтительнее, чем с а1а3а8)
Элементы qi появляются в А ближе друг к другу. (В примере – совпадение q1q2q3 с а2а3а4 предпочтительнее, чем с а1а3а5)
Из двух контекстов документа, одинаково совпадающих с контекстом запроса, выше оценивается тот, который имеет меньшую длину.

Схожесть контекстов
POS(Q,A)
POS(Q,A) = 1-((AP-AverOptimalPosition)/(|A|-2*AverOptimalPosition+1))
AverOptimalPosition - среднее положение оптимального совпадения Q и А (если совпадение начинается с первого элемента и продолжается без пробелов)
АР - фактическое среднее положение совпадения Q и А
0 ≤ POS(Q,A) ≤ 1
(0 – в случае полного несовпадения, 1 – в случае «самого левого»
совпадения)

Схожесть контекстов
GAPS(Q,A)
GAPS(Q,A) = gaps/(gaps + lcs(Q,A))
gaps - число «пробелов» (в примере gaps = 4)
0 ≤ GAPS ≤ 1
( 0 – полное совпадение)

Схожесть контекстов
LD(Q,A)
LD(Q,A)= (|A|- lcs(Q,A))/|A|
0 ≤ LD ≤ 1
( 0 – полное совпадение)

Схожесть контекстов
cr(Q,A) = αLCS(Q,A) + βPOS(Q,A) – γGAPS(Q,A) – δLD(Q,A)
0 ≤ α ≤ 1, 0 ≤ β ≤ 1, 0 ≤ γ ≤ 1, 0 ≤ δ ≤ 1
α + β = 1 (т.к. cr(Q,A) = 1 в случае полного совпадения)

Примеры
Показывают, как влияют оценки LCS(Q,A) , POS(Q,A), GAPS(Q,A), LD(Q,A) на cr(Q,A)
Q = q1q2q3 = book/chapter/title
Положим α = 0.75, β = 0.25, γ = 0.25, δ = 0.2
Для простоты будем рассматривать lcs(Q,A) вместо LCS(Q,A),
АР вместо POS, gaps вместо GAPS, ld вместо LD

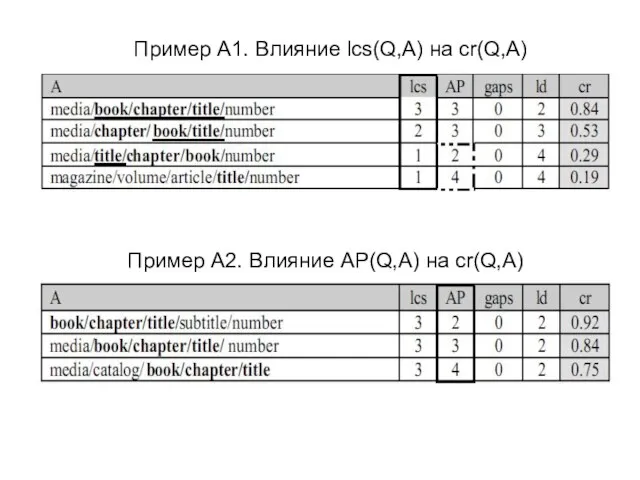
Пример A1. Влияние lcs(Q,A) на cr(Q,A)
Пример A2. Влияние AP(Q,A) на cr(Q,A)

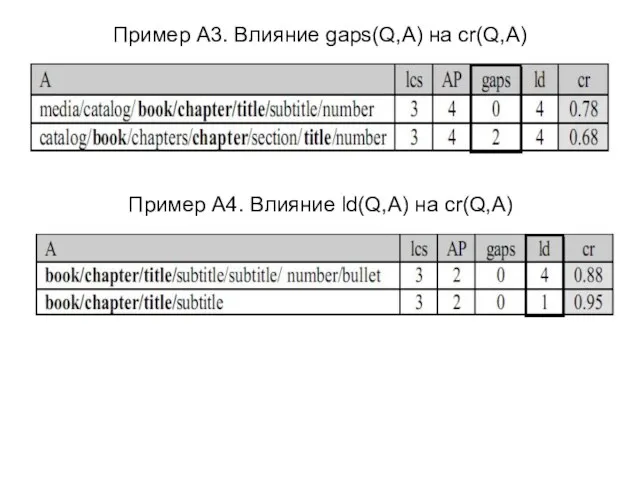
Пример A3. Влияние gaps(Q,A) на cr(Q,A)
Пример A4. Влияние ld(Q,A) на cr(Q,A)

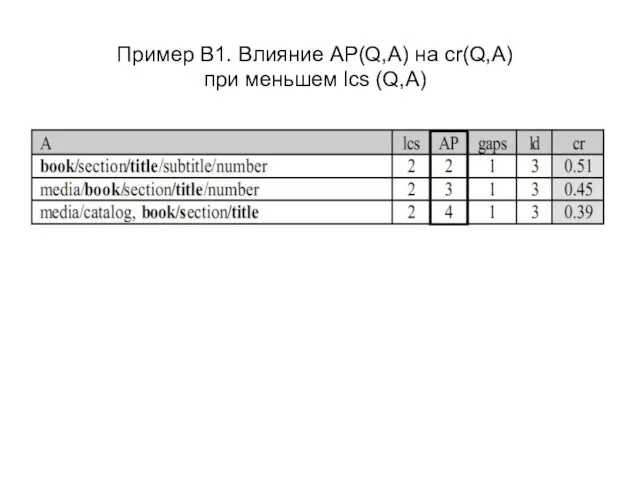
Пример B1. Влияние AP(Q,A) на cr(Q,A)
при меньшем lcs (Q,A)

Okapi BM25
d - документ
C – коллекция документов
W(d,q,C) – релевантность документа d из коллекции С запросу q
wj(d,C) – вес j-го терма в документе d коллекции С
qj – совпадание терма j из документа с термом запроса

Okapi BM25
d - документ
C – коллекция документов
wj(d,C) – вес j-го терма в документе d коллекции С
tfj – частота j-го терма в документе d коллекции С (TF)
dfj – количество документов коллекции, содержащих j-й терм
dl – длина документа
avdl – средняя длина документов в коллекции
k1, b – коэффициенты (обычно k1 = 2, b = 0.75)

BM25F
модификация BM25, в которой документ рассматривается как совокупность нескольких полей (таких как, например, заголовки, основной текст, ссылочный текст), длины которых независимо нормализуются, и каждому из которых может быть назначена своя степень значимости в итоговой функции ранжирования.
tf’j – взвешенная частота j-го терма в документе d
dl’ – взвешенная длина документа
avdl’ – взвешенная средняя длина документа
k’1 – взвешенный параметр

BM25F
Пусть имеется nF полей f = 1, …, nF
В данном поле f документа d терм t имеет частоту tfd,t,f
Пусть V – это словарь (набор термов). Тогда
Длина поля f в документе d
Частота терма t в документе d

BM25F
Пусть имеется nF полей f = 1, …, nF
В данном поле f документа d терм t имеет частоту tfd,t,f
Пусть V – это словарь (набор термов). Тогда
Длина документа d
Средняя длина документа

BM25F
Если считать, что полю f присвоен вес wf , получим:
N – мощность коллекции
atf – средняя частота терма

BM25E
В BM25F вместо частоты терма в документе используется линейная комбинация взвешенных частот терма в полях
Этот метод можно применить к поиску элементов.
Элементы можно обрабатывать так же, как и документы. Но каждый элемент может иметь ещё и дополнительные, унаследованные поля

BM25E
Пусть имеется nЕ элементов е = 1, …, nЕ в коллекции С
В элементе е терм t имеет частоту tfd,t,e
el – длина элемента
avel – средняя длина элемента
Тогда расширение ВМ25 на случай поиска элементов:

ВМ25Е
Соответственно, функция ВМ25Е:
tf’e,j – взвешенная частота j-го терма в элементе е
еl’ – взвешенная длина элемента
avеl’ – взвешенная средняя длина элемента в коллекции
k’1 – взвешенный параметр

BM25E
Соответственно,
M – мощность коллекции
atf – средняя частота терма

Литература
Christopher D. Manning, Prabhakar Raghavan and Hinrich Schütze, Introduction to Information Retrieval, Cambridge University Press. 2008.
David Carmel, Nadav Efraty, Gad M. Landau, Yoelle S. Maarek, Yosi Mass, An Extension of the Vector Space Model for Querying XML Documents via XML Fragments, ACM SIGIR'2002 Workshop on XML and IR, Tampere, Finland , Aug 2002
Wei Lu, Stephen Robertson, Andrew Macfarlane, Advances in XML Information Retrieval and Evaluation (INEX 2005). LNCS 3977, Springer 2006 (pp 161-171).