Слайд 2Содержание:
Введение 3
1. Составные части задачи и требования по ее решению в

школьном
курсе математики 4
2.Метод математического моделирования при решении текстовых задач. 6
2.1. Понятие модели и моделирования. 6
2.2. Моделирование при решении задач. 10
2.2.1.Задачи на встречное движение двух тел. 13
2.2.2.Задачи на движение двух тел в одном направлении. 14
2.2.3.Задачи на движение двух тел в противоположных направлениях. 15
2.3.Опытно-практическая работа по сопоставлению применяемых
способов решения задач в 5 и 9 классов. 17
Заключение 18
Приложение.
Список литературы.
Слайд 3Методы решения задач
- анализ и синтез
- метод сведения к ранее решённым
- метод

математического
моделировавния
- метод математической индукции
- метод исчерпывающих проб
Слайд 4Метод математического моделирования
«В процессе математического моделирования выделяют три этапа:
1. Формализация –

перевод предложенной задачи (ситуации) на язык
математической теории (построение математической модели задачи).
2. Решение задачи в рамках математической теории (говорят: решение внутри модели).
3.Перевод результата математического решения задачи на тот язык, на котором была сформулирована исходная задача (интерпретация решения).»
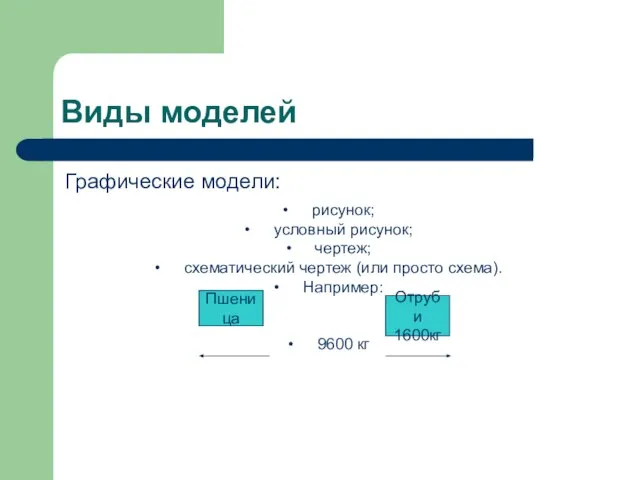
Слайд 5Виды моделей
Графические модели:
рисунок;
условный рисунок;
чертеж;
схематический чертеж (или просто схема).
Например:
9600 кг
Пшеница
Отруби
1600кг
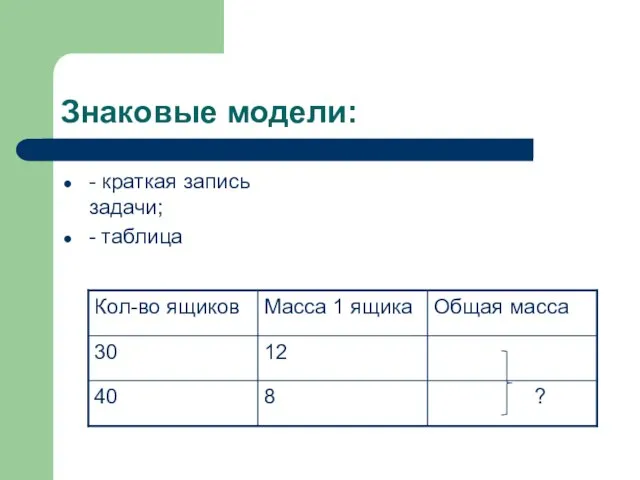
Слайд 6Знаковые модели:
- краткая запись задачи;
- таблица
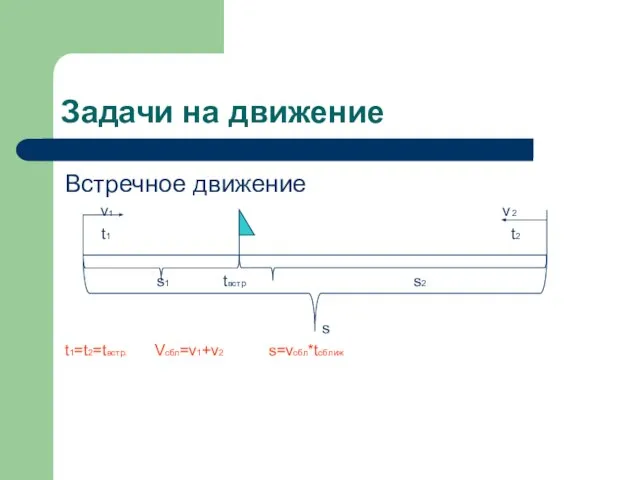
Слайд 7Задачи на движение
Встречное движение
v1 v2
t1 t2
s1 tвстр s2
s
t1=t2=tвстр. Vсбл=v1+v2 s=vсбл*tсближ
Слайд 8Движение в одном направлении
v1 v2
t1 t2
s s2
s1 vсближ =v1-v2,.s=s1-s2 ,
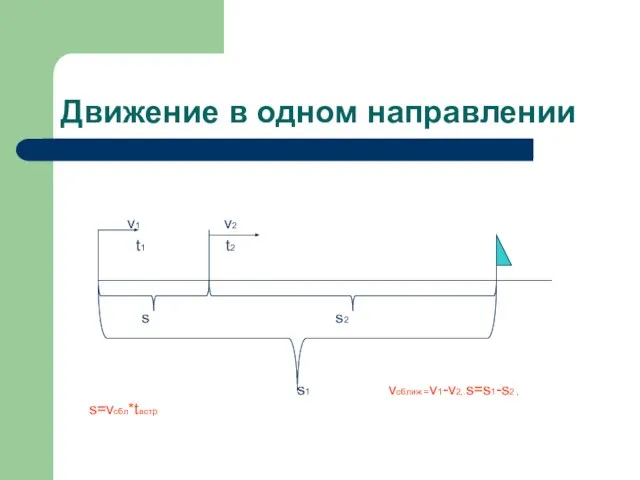
s=vсбл*tвстр
Слайд 9Движение в противоположных направлениях
В таких задачах два тела могут начинать движение в

противоположных направлениях из одной точки:
а) одновременно;
б) в разное время.
А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.
Общим теоретическим положением для них будет следующее:
v удал. = v1+ v2, где v1 и v2 соответственно скорости первого и второго тел.
(Схематический чертеж строится аналогично предыдущим).








 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва