МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Колебания - это движения или изменения состояния, обладающие той или иной степенью повторяемости.

Свободные гармонические колебания
Свободными собственными механическими колебаниями называют колебания, которые происходят без переменных внешних воздействий на колебательную систему и возникают вследствие начального смещения из положения равновесия или сообщения системе начальной скорости.

Гармонические колебания.
Колебания называются периодическими, если значения всех изменяющихся величин, характеризующих систему, повторяются через равные промежутки времени. Наименьший промежуток времени, удовлетворяющий этому условию называется периодом колебаний Т.

В качестве примера рассмотрим идеальный пружинный маятник
Рис. 1. Пружинный маятник

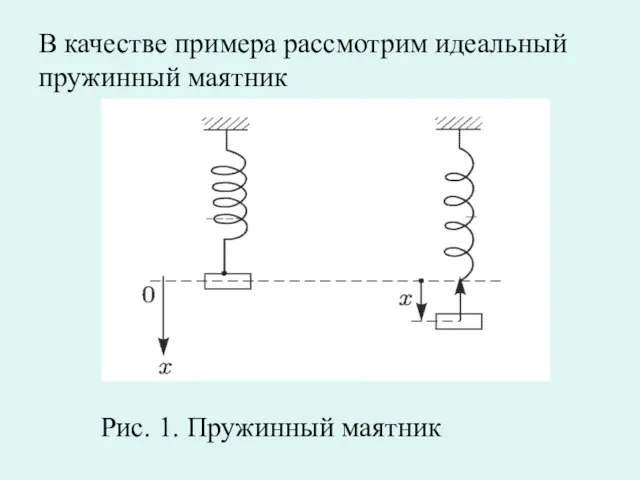
Если пружину оттянуть (сжать) на расстояние х от положения равновесия, то сила упругости, с которой деформированная пружина действует на внешнее тело, определяется законом Гука:
F = - k x (1)
где k - жесткость пружины, зависящая от ее размеров и материала, а знак « - » показывает, что сила упругости всегда направлена в сторону, противоположную направлению смещения, то есть к положению равновесия.

Предположим, что силы сопротивления отсутствуют. Тогда, подставив выражение (1) в формулу второго закона Ньютона
(ma = F), получим дифференциальное уравнение свободных колебаний при отсутствии трения:
(2)

Преобразуем выражение (2) следующим образом:
и получим дифференциальное уравнение второго порядка:
(3)
где

Общее решение уравнения (3) представляет периодическую функцию и может быть записано в одном из двух видов:
или (4)

Гармонические колебания — такие, при которых наблюдаемая величина изменяется во времени с определенной частотой по закону синуса или косинуса.

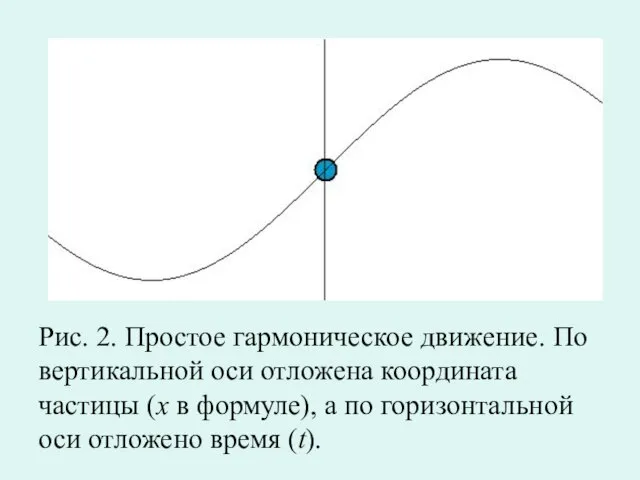
Рис. 2. Простое гармоническое движение. По вертикальной оси отложена координата частицы (x в формуле), а по горизонтальной оси отложено время (t).

Рис . 3.Система груз-пружина без затухания, в которой происходит простое гармоническое движение.

Величины, входящие в формулу (4), имеют следующий смысл:
х — смещение точки от положения равновесия в момент времени t;
А — амплитуда колебаний (максимальное смещение от положения равновесия);
ω0 — собственная круговая (циклическая) частота колебаний (число колебаний, совершаемых за 2π секунд);
φ = (ω0t + φ0) — фаза колебаний (в момент времени t);
φ0— начальная фаза колебаний (при t = 0).

Частота колебаний ν (число колебаний, совершаемых за единицу времени) равна
(5)
Период колебаний Т — это время, в течение которого совершается одно полное колебание:
(6)
Связь между указанными характеристиками определяется формулами:
(7)

Зная закон движения, можно определить скорость и ускорение колеблющегося тела в любой момент времени: υ = dx/dt, a = dv/dt. Для случая φ0= 0 получим:
(8)
где υmax — максимальная скорость (амплитуда скорости);
(9)
где amax — максимальное ускорение (амплитуда ускорения).

Колеблющееся тело в любой момент времени обладает кинетической энергией собственного движения — Ек и потенциальной энергией Еп, связанной с деформацией пружины.
Полная энергия колеблющегося тела складывается из его кинетической и потенциальной энергий:
(10)

Механические волны и их виды
Процесс распространения механических колебаний в упругой среде называется упругой, или механической, волной.
При распространении механической волны сами частицы среды не перемещаются вместе с ней, а колеблются около своих положений равновесия. Поэтому распространение волны не сопровождается переносом вещества!

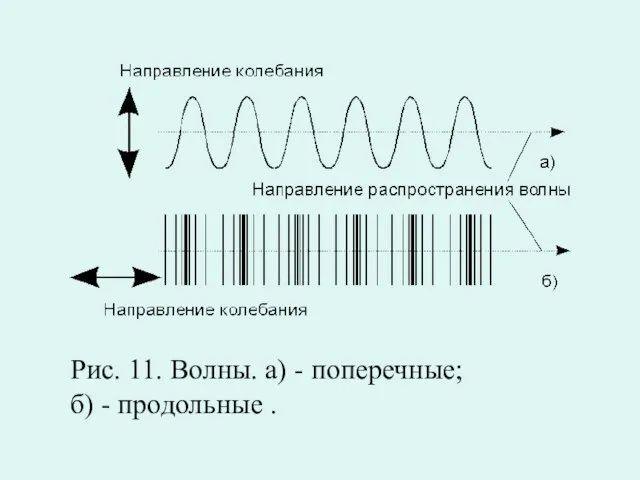
Продольные волны — такие, в которых частицы среды колеблются вдоль направления распространения колебаний. При этом в среде чередуются области сжатия и разряжения.
Поперечные волны — такие, в которых частицы колеблются перпендикулярно к направлению распространения колебаний. При этом в среде возникают периодические деформации сдвига.

Рис. 11. Волны. а) - поперечные;
б) - продольные .

Фронт волны — геометрическое место точек (поверхность), в которых фаза колебаний имеет одно и то же значение. Для всех точек фронта время, за которое до них дошло возмущение, одинаково.
Скоростью волны υ называется скорость перемещения ее фронта.

Плоской называется волна, у которой фронтом является плоскость, перпендикулярная направлению распространения.
Сферической называется волна, у которой фронт имеет форму сферы.

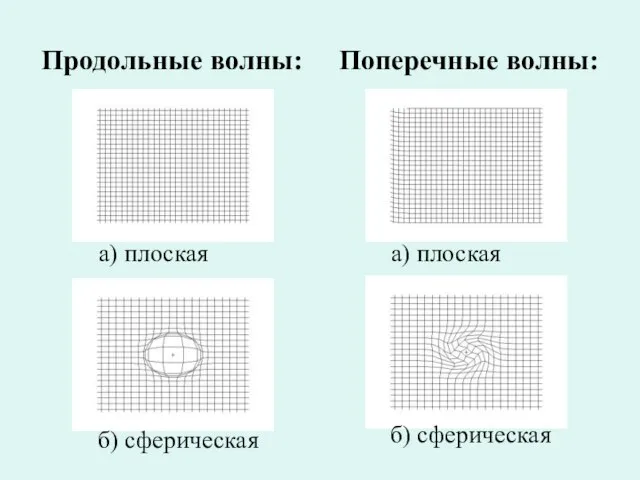
Продольные волны: Поперечные волны:
а) плоская
а) плоская
б) сферическая
б) сферическая

Частота волны. Уравнение плоской волны
Волна возникает в результате периодических внешних воздействий на среду. Если источник, создающий волну, колеблется по гармоническому закону с некоторой частотой v, то точки среды вовлекаются в колебательное движение с такой же частотой. Эта частота называется частотой волны.

Уравнение , определяющее смещение любой точки среды в любой момент времени, называется уравнением плоской волны.
(11)
Аргумент при косинусе — величина
φ= ω(t — s/υ) называется фазой волны.
Обычно вместо круговой частоты колебаний ω указывают частоту ν или период колебаний точек среды Т.

Длина волны
Длиной волны называется расстояние, на которое перемещается ее фронт за время равное периоду колебаний частиц среды:
λ = υT. (12)
Обычно в качестве характеристики волны используют не период колебаний (Т), а их частоту (v = 1/Т) и формулу для длины волны записывают в виде
λ = υ/v (13)

Энергетические характеристики волны
Поток энергии (Ф) — величина, равная средней энергии, проходящей за единицу времени через данную поверхность:
Ф = dE/dt [Вт] (14)
Объемная плотность энергии (wp) — средняя энергия колебательного движения, приходящаяся на единицу объема среды:
wp = ρA2ω2/2 [Дж/м3], (15)
где ρ — плотность среды.

Интенсивность волны (плотность потока энергии волны) (I) — величина, равная потоку энергии волны, проходящей через единичную площадь, перпендикулярную к направлению распространения волны:
I = Ф/S [Вт/м2] (16)
или
I = υρA2ω2/2

Некоторые специальные разновидности волн
Ударная волна — это распространяющаяся со сверхзвуковой скоростью тонкая переходная область, в которой происходит резкое возрастание плотности вещества и скорости движения частиц среды; это распространение скачка уплотнения со сверхзвуковой скоростью.

Эффект Доплера и его использование в медицине
Эффект Доплера состоит в том, что воспринимаемая приемником частота v отличается от излучаемой источником частоты v0 вследствие движения источника волн и приемника.
При приближении объекта к датчику частота отраженного сигнала увеличивается, а при удалении - уменьшается.

Звук, виды звука
Звук в широком смысле — упругие колебания и волны, распространяющиеся в газообразных, жидких и твердых веществах; в узком смысле — явление, субъективно воспринимаемое органом слуха человека и животных. В норме ухо человека слышит звук в диапазоне частот от 16 Гц до 20 кГц.

Звук с частотой ниже 16 Гц называется инфразвуком, выше 20 кГц — ультразвуком, а самые высокочастотные упругие волны в диапазоне от 109 до 1012 Гц — гиперзвуком.

Звуковой удар - это кратковременное звуковое воздействие (хлопок, взрыв, удар, гром).
Тон — это звук, представляющий собой периодический процесс. Основной характеристикой тона является частота.
Акустический спектр тона — это совокупность всех его частот с указанием их относительных интенсивностей или амплитуд.

Шум — это звук, имеющий сложную, неповторяющуюся временную зависимость, и представляет собой сочетание беспорядочно изменяющихся сложных тонов.
Сложные тоны имеют дискретный спектр, а шум – сплошной.

Физические характеристики звука
Скорость (υ). Звук распространяется в любой среде, кроме вакуума. Скорость его распространения зависит от упругости, плотности и температуры среды, но не зависит от частоты колебаний.

Интенсивность (I). Это энергетическая характеристика звука. По определению — это плотность потока энергии звуковой волны. Для уха человека важны два значения интенсивности (на частоте 1 кГц):
порог слышимости — это минимальное значение интенсивности звука воспринимаемое нормальным человеческим ухом I0 = 10-12 Вт/м2
порог болевого ощущения — Imax = 10 Вт/м2, звук такой интенсивности человек перестает слышать и воспринимает его как ощущение давления или боли.

Звуковое давление (Р) — это давление, дополнительно возникающее при прохождении звуковой волны в среде; оно является избыточным над средним давлением среды.
Между интенсивностью (I) и звуковым давлением (Р) существует связь: I = P2/2ρυ

Уровень интенсивности. При сравнении интенсивности звука удобно пользоваться логарифмической шкалой, то есть сравнивать не сами величины, а их логарифмы. Для этого используется специальная величина— уровень интенсивности (L):
L =lg(I/I0) = 2lg(P/P0).
Единицей измерения уровня интенсивности является — бел, [Б]

Характеристики слухового ощущения, звуковые измерения
Высота тона обусловлена, прежде всего, частотой основного тона (чем больше частота, тем более высоким воспринимается звук). В меньшей степени высота зависит от интенсивности волны (звук большей интенсивности воспринимается более низким).

Тембр звука определяется его гармоническим спектром. Различные акустические спектры соответствуют разному тембру, даже в том случае, когда основной тон у них одинаков. Тембр — это качественная характеристика звука.
Громкость звука — это субъективная оценка уровня его интенсивности.

Закон Вебера-Фехнера.
Если увеличивать раздражение в геометрической прогрессии (то есть в одинаковое число раз), то ощущение этого раздражения возрастает в арифметической прогрессии (то есть на одинаковую величину).
Cубъективное восприятие интенсивности звука связано не только с уровнем интенсивности, но и с частотой звука.

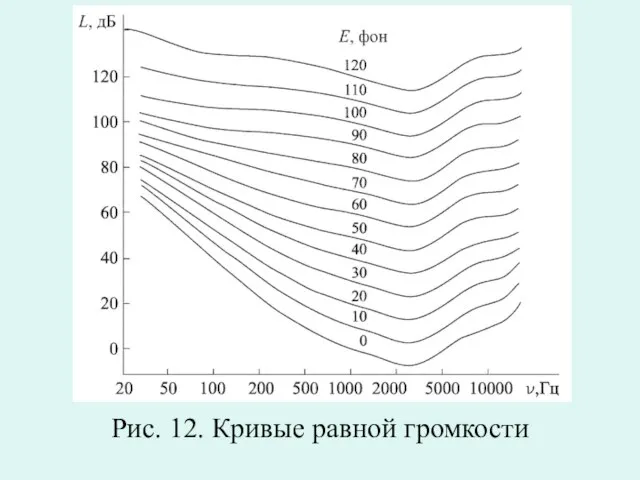
Для звука с частотой 1 кГц вводят единицу уровня громкости — фон, которая соответствует уровню интенсивности 1 дБ.
Громкость звука равна уровню интенсивности звука (дБ) на частоте 1 кГц, вызывающего у «среднего», человека такое лее ощущение громкости, что и данный звук.

Рис. 12. Кривые равной громкости

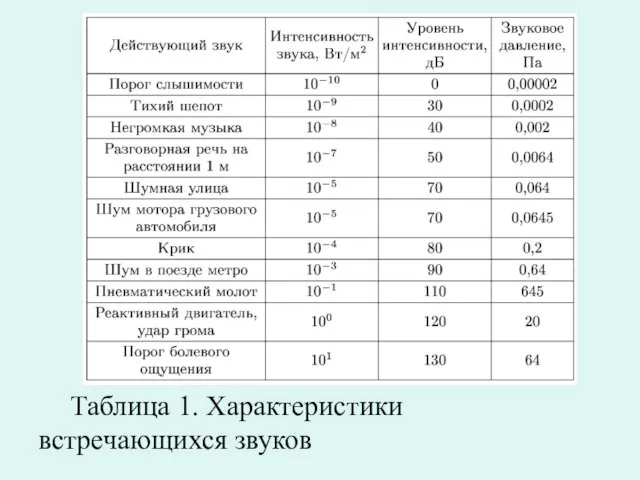
Таблица 1. Характеристики встречающихся звуков