МЕТОД ЗОЛОТОГО СЕЧЕНИЯ

Метод золотого сечения состоит в построении последовательности отрезков [a0,b0],[a1,b1],...,
стягивающихся к точке минимума функции f(x). На каждом шаге, за исключением первого, вычисление значения функции f(x) проводится лишь один раз. Эта точка, называемая золотым сечением, выбирается специальным образом.

На первом шаге процесса оптимизации внутри отрезка [a0,b0] выбираем две внутренние точки x1 и x2 и вычисляем значения целевой функции f(x1) и f(x2). Поскольку в данном случае f(x1)< f(x2), очевидно что
минимум расположен на одном из прилегающих к x1 отрезков [a0, x1] или [x1, x2]. Поэтому отрезок [x2, b0] можно отбросить, сузив тем самым первоначальный интервал неопределенности.
a0
b0
x1
x2
f(x1)
f(x2)

Второй шаг проводим на отрезке [a1, b1], где a1=a0, b1= x2. Нужно снова выбрать две внутренние точки, но одна из них (x1) осталась из предыдущего шага, поэтому достаточно выбрать лишь одну точку x3 , вычислить значение f(x3) и провести сравнение.
Поскольку здесь f(x3)>f(x1), ясно, что минимум находится на отрезке [x3, b1].
Обозначим этот отрезок [a2, b2], снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длина очередного отрезка [an, bn] не станет меньше заданной Е.
a1= a0
b1=x2
f(x3)
f(x1)

Рассмотрим способ размещения внутренних точек на каждом отрезке [ak, bk]. Пусть длина интервала неопределенности равна L, а точка деления делит его на части L1, L2: L1 > L2, L= L1 + L2. Золотое сечение интервала неопределенности выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка:
L1 /L= L2/ L1

Из этого соотношения можно найти точку деления, определив отношение L2/L1. Преобразуем равенство и найдем значение L2/L1 :
L1²=L2*L, L1²=L2*(L1+L2),
L2²+L1*L2-L1²=0,
(L2/L1)²+L2/L1-1=0,
L2/L1 =(-1+√5)/2 и L2/L1 =(-1-√5)/2,
Поскольку нас интересует только положительное решение, то
L2/L1 = L1/L=(-1+√5)/2≈0.618
L1≈0.618L, L2≈0.382L

Поскольку заранее неизвестно, в какой последовательности (L1 и L2 или L2и L1) делить интервал неопределенности, то рассматривают внутренние точки, соответствующие двум этим способам деления. На рисунке точки деления x1и x2 выбираются с учетом полученных значений для
частей отрезка. В данном случае имеем
x1-a0=b0-x2= 0.382d0,
b0-x1=x2-a0=0.618d0,
d0=b0-a0.
a0
b0
x1
x2

После первого шага оптимизации получается новый интервал неопределенности – отрезок [a1, b1]
Можно показать, что точка x1 делит этот отрезок в требуемом отношении, при этом
b1-x1=0.382d1, d1=b1-a1
Проведем преобразования:
b1-x1=x2-x1=x2-x1 +d0-d0=x2-x1+ b0-a0- b0 +a0=(b0-a0)-(x1-a0)-(b0-x2)=d0-0.382d0-0.382d0=0.236d0,
d1=x2-a0=0.618d0,
b1-x1=0.236(d1/0.618)=0.382d1
a1=a0
b1= x2
x3
x1

Вторая точка деления x3 выбирается на таком же расстоянии от левой границы отрезка, т.е.
x3-a1=0.382d1
И снова интервал неопределенности уменьшается до размера
d2=b2-a2=b1-x3=0.618d1=(0.618)²d0
Используя полученные соотношения, можно записать координаты точек деления y и z отрезка [ak,bk] на (k+1)-м шаге оптимизации (y
y-ak=0.382* dk
y=ak +0.382(bk-ak)=0.618*ak+0.382*bk
bk -z =0.382* dk
z= bk- 0.382(bk-ak)=0.382*ak+0.618*bk
При этом длина интервала неопределенности равна
dk=bk-ak=(0.618)kd0

Процесс оптимизации заканчивается при выполнении условия dk ak
Можно в качестве оптимального значения принять x=ak (или x=bk, x=(ak+bk)/2 и т.п.)
Блок-схема процесса одномерной оптимизации методом золотого сечения
y,z-точки деления отрезка [a,b],y

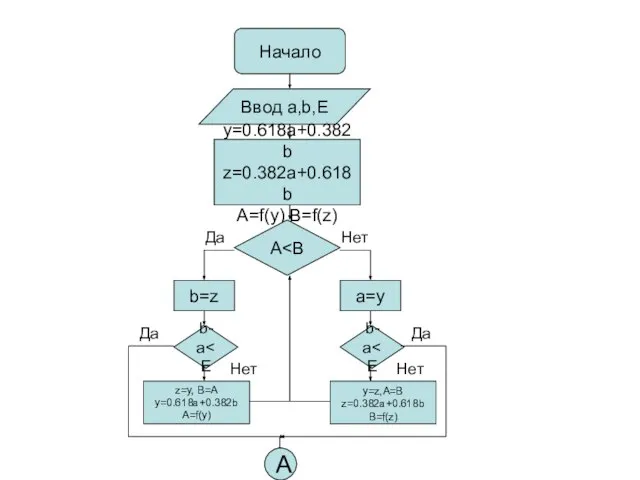
Начало
Ввод a,b,E
y=0.618a+0.382b
z=0.382a+0.618b
A=f(y),B=f(z)
A
a=y
b-a
y=z,A=B
z=0.382a+0.618b
B=f(z)
b=z
b-a
z=y, B=A
y=0.618a+0.382b
A=f(y)
A
Нет
Да
Да
Да
Нет
Нет

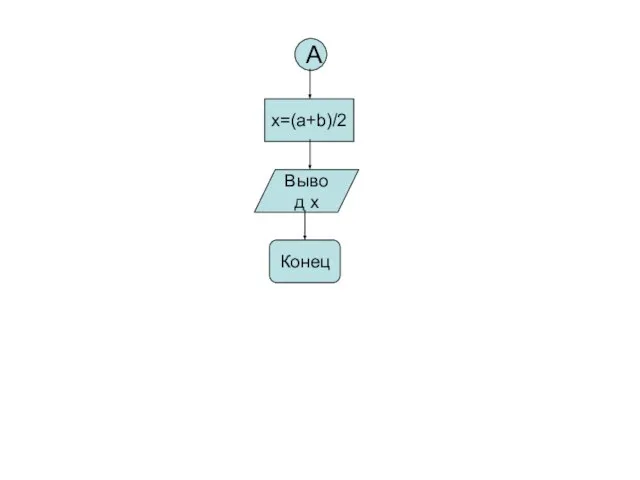
A
x=(a+b)/2
Вывод x
Конец

Пример
Для оценки сопротивления дороги движению автомобиля при скорости V км/ч можно использовать эмпирическую формулу f(V)=24-2/3*V+1/30*V². Определить скорость, при которой сопротивление будет минимальным.
Решение
Это задача одномерной оптимизации. Здесь сопротивление f(V)- целевая функция, а V-проектный параметр. Данную задачу легко решить путем нахождения минимума с помощью производной, поскольку данная функция дифференцируемая.
f′(V)=2/3+2*V/30=0
V=10 км/ч

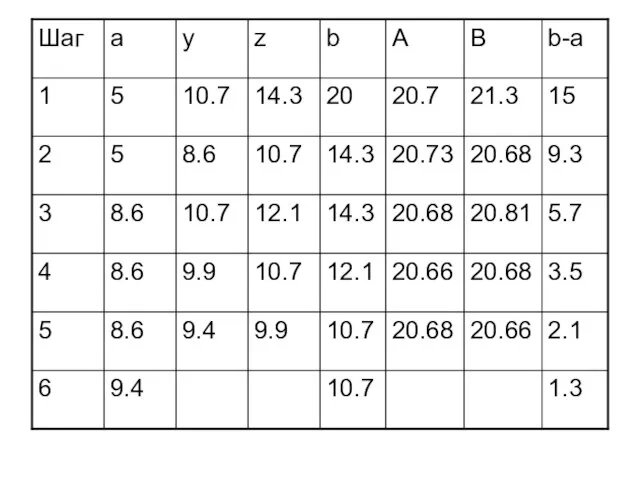
А теперь решим задачу методом золотого сечения. Пусть границы интервала равны:a=5,b=20. Расчеты проводятся в соответствии с блок-схемой с погрешностью E=1км/ч. Результаты решения приведены в виде таблицы.