Мир Многогранников

Многогранником называется ограниченное тело, поверхность которого состоит из конечного числа многоугольников.
Виды многогранников:
1 Платоновы тела
2 Архимедовы тела
3 Тела Кеплера-Пуансо
Многогранники в архитектуре
Многогранники в искусстве

Платоновы тела
Многогранник называется правильным, если:
он выпуклый,
все его грани равные друг другу правильные многоугольники
в каждой его вершине сходится одинаковое число граней.
По-другому правильные многогранники называются Платоновы тела.

Начиная с 7 века до нашей эры в Древней Греции создаются философские школы , в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.
Существование пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды.
А так как пятой стихии в природе не было, то по их учению додекаэдр представлял собой всю Вселенную, то есть они считали, что мы живём внутри небесного свода, имеющего форму поверхности правильного додекаэдра.
Пять элементов

Огонь

Вода

Воздух

Земля

Вселенная

Тетраэдр
Каждая грань многогранника – правильный треугольник.
Это многогранник называется правильный тетраэдр.

Гексаэдр
Каждая грань многогранника – квадрат.
Этот многогранник называется правильный гексаэдр или куб.

Октаэдр
Каждая грань многогранника – правильный треугольник.
Этот многогранник называется правильный октаэдр.

Додекаэдр
Каждая грань многогранника – правильный пятиугольник.
Этот многогранник называется правильный додекаэдр.

Икосаэдр
Каждая грань многогранника – правильный треугольник.
Этот многогранник называется правильный икосаэдр.

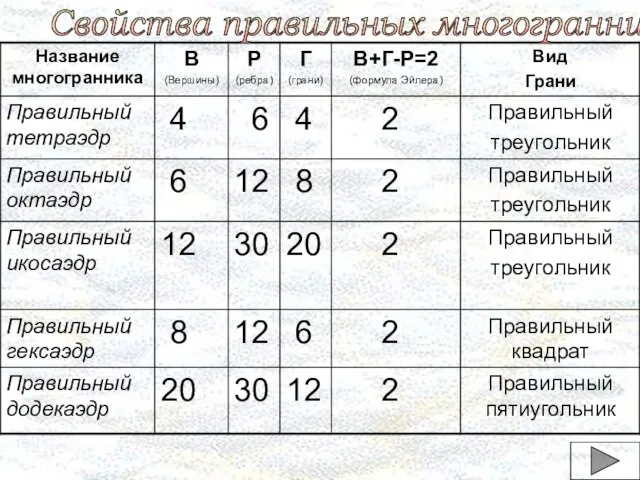
Свойства правильных многогранников

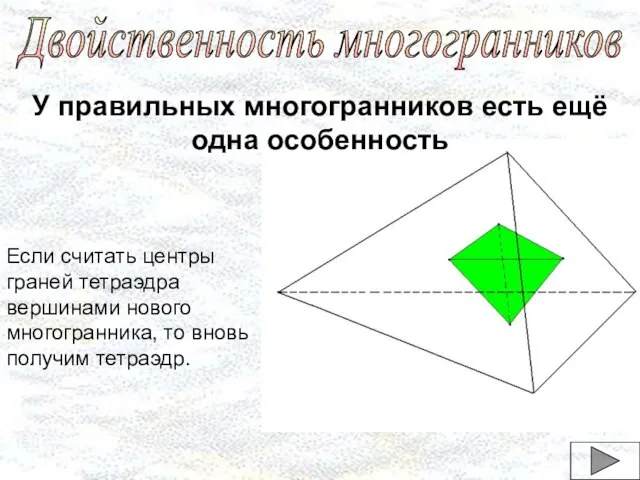
Двойственность многогранников
У правильных многогранников есть ещё одна особенность
Если считать центры граней тетраэдра вершинами нового многогранника, то вновь получим тетраэдр.

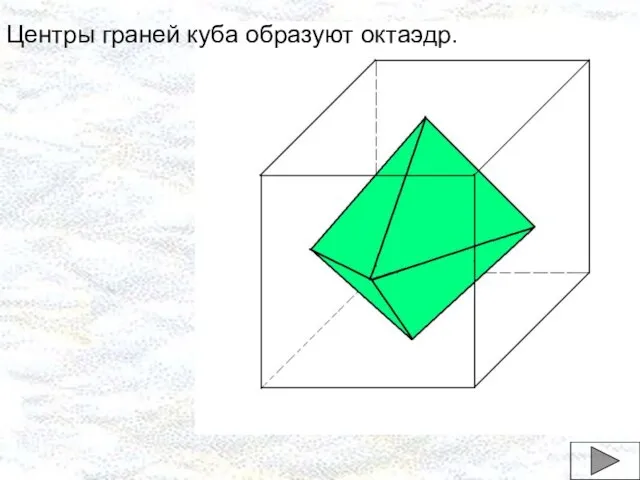
Центры граней куба образуют октаэдр.

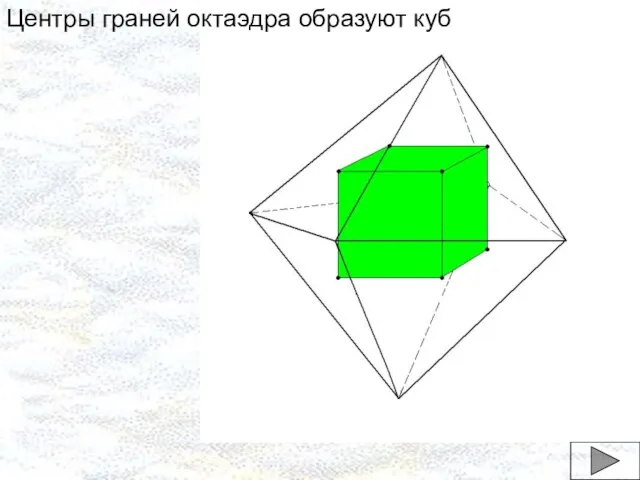
Центры граней октаэдра образуют куб

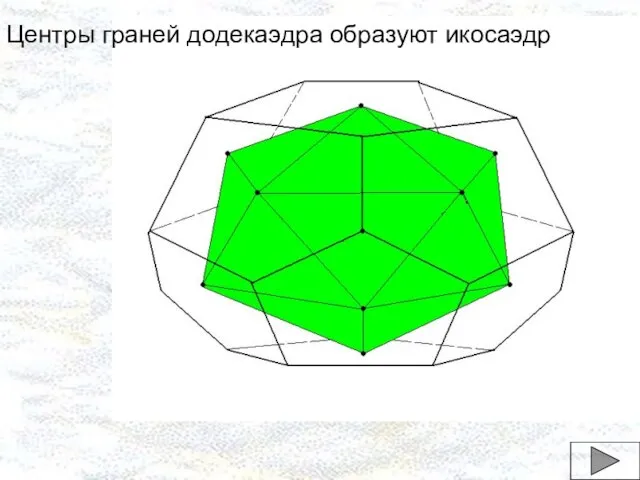
Центры граней додекаэдра образуют икосаэдр

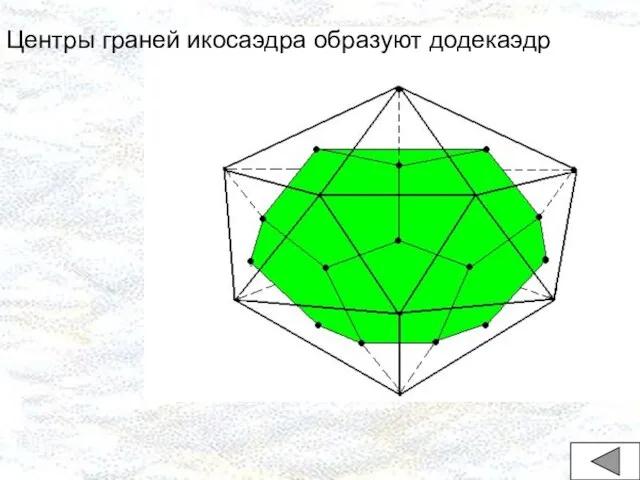
Центры граней икосаэдра образуют додекаэдр

Архимедовы тела
Из правильных многогранников (Платоновы тела) можно получить так называемые полуправильные многогранники, или Архимедовы тела. Гранями их являются также правильные, но разноимённые многоугольники.
Открытие тринадцати полуправильных многогранников приписывается Архимеду, впервые перечислившего их в недошедшей до нас работе.

Усечённый октаэдр
Курносый куб
Кубоктаэдр

Усечённый тетраэдр
Усечённый икосаэдр
Усечённый куб

Усечённый додекаэдр
Ромбокубоктаэдр
Ромбоикосододекаэдр

Ромбоусечённый икосододекаэдр
Курносый додекаэдр
Ромбоусечённый кубоктаэдр
Иосододекаэдр

Псевдоромбокубоктаэдр
Относительно недавно (в конце 50-х - начале 60-х годов XX века) несколько математиков практически одновременно, независимо друг от друга указали на существование еще одного, ранее неизвестного полуправильного выпуклого многогранника - псевдоромбокубоктаэдра. Однако не все специалисты согласны с причислением этого многогранника к архимедовым телам.

Тела Кеплера-Пуансо
Тела Архимеда получаются из правильных многогранников с помощью операции (усечения), то есть отсечения углов плоскостями, и они тоже являются выпуклыми многогранниками. А продолжение их граней и рёбер позволяет получить звёздчатые многогранники, которые являются не выпуклыми. Их ещё называют телами Кеплера-Пуансо.
Было предложение Кеплера рассматривать невыпуклые многогранники со звёздчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдра. Поэтому эта группа многогранников носит название тела Кеплера - Пуансо.

Звёздчатый октаэдр
Он был открыт Леонардо Да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером и назван им (звезда восьмиугольная). У октаэдра есть только одна звездчатая форма. Её можно рассматривать как соединение двух тетраэдров.

Большой звёздчатый додекаэдр
Большой звездчатый додекаэдр принадлежит к семейству тел Кеплера-Пуансо, то есть правильных невыпуклых многогранников. Грани большого звездчатого додекаэдра – пентаграммы, как и у малого звездчатого додекаэдра. У каждой вершины соединяются три грани. Вершины большого звездчатого додекаэдра совпадают с вершинами описанного додекаэдра.
Большой звездчатый додекаэдр был впервые описан Кеплером в 1619 г. Это последняя звездчатая форма правильного додекаэдра.

Икосаэдр
Икосаэдр имеет 20 граней. Если каждую из них продолжить неограниченно, то тело будет окружено великим многообразием отсеков-частей пространства, ограниченных плоскостями граней. Все звёздчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства 20+30+60+120+20+60+12+30+60+60 отсеков десяти различных форм и размеров. Большой икосаэдр состоит из всех этих кусков, за исключением последних шестидесяти.

Икосододекаэдр
Икосододекаэдр имеет 32 грани, из которых 12 являются правильными пятиугольными гранями, а остальные 20 – правильные треугольники. Что касается вопроса о том, могут ли получившиеся многогранники оказаться правильными, то на него давно получен ответ. Великий математик Каши ещё в 1811 году доказал, что список правильных многогранников исчерпывается пятью Платоновыми телами вкупе с четырьмя многогранниками Кеплера - Пуансо.

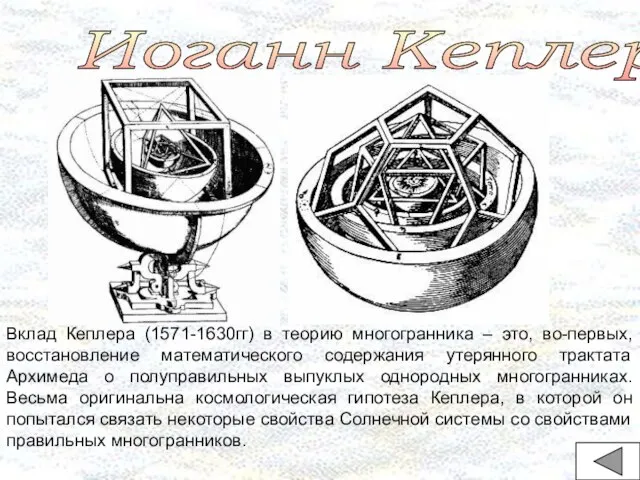
Иоганн Кеплер
Вклад Кеплера (1571-1630гг) в теорию многогранника – это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках. Весьма оригинальна космологическая гипотеза Кеплера, в которой он попытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников.

Многогранники в архитектуре
Музей Плодов в Яманаши Ицуко Хасегава

Великая пирамида в Гизе

Великие пирамиды в Гизе

Александрийский маяк

Фаросский маяк

Один из Японских музеев

Многогранники в искусстве
Альбрехт Дюрер «меланхолия»

ромбододекаэдр
Ромбоидальный или ромбический додекаэдр – это двенадцатигранник, гранями которого являются ромбы.
Форму этого многогранника придумал не сам человек, а создала сама природа в виде кристалла граната.