М.Lvov About one Approach for Designing of Algebraic Computations: Computations in Boolean Algebra. Designing of algorithms for algebraic computations – the main task arising when realising mathematical systems based on symbolic tra
Содержание
- 2. Theory and detailes in: Lvov М.S. Synthesis of Interpreters of Algebraic Operations in Extensions of Multisorted
- 3. Approach IEM Inheritance, Extensions, Morphisms Base principles and ideas of IEM are quite simple and well
- 4. Algebraic programming system APS (V. Peschanenko) APS uses technologies of algebraic programming, based on rewriting rules
- 5. Compute the value of logical expression in signature of logical operations By the value of expression
- 6. Traditional logical canonical forms are PDNF, PCNF. We shell use Recursive Normal Form (RNF). Paradigm of
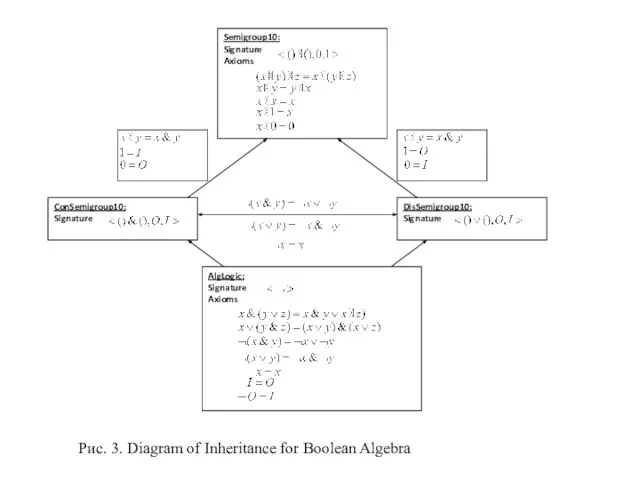
- 7. Method of Inheritance In algebraic computations are used: Classical (axiomatically of constructively defined) algebraic structures, Algebraic
- 9. Axiomatic descriptions plays constructive role. Its defines signatures, computations with constants. Inheritance is used for definitions
- 10. Аbstract Algorithms Inheritance is used for descriptions of algorithms on abstract level (independently of algebras support).
- 11. Method of Extensions Axiomatic definition of sort AlgLogic is initial for further development. Three constructive models
- 15. Additional Rules (partial cases): In the rule (10) suppose A1 = B1. then obtain: A1 ∨
- 16. Dis := rs(A1, B1, A2, B2, x) { L(A1, B1, x) ∨ L(A2, B2 , x)
- 17. Main Result of Extension’s Method Definition of algebra as direct limit of increasing sequence of algebras
- 23. Скачать презентацию



















 Стандарт cXML в корпоративных приложениях электронной коммерции
Стандарт cXML в корпоративных приложениях электронной коммерции Натюрморт в фотографии
Натюрморт в фотографии Золотой век русской культуры. Литература. Живопись
Золотой век русской культуры. Литература. Живопись титул констатирующего
титул констатирующего Повесть о настоящем человеке
Повесть о настоящем человеке Выпускающая кафедра«Механика механизмов и машин» Заведующий кафедрой Шевченко Игорь Владимирович
Выпускающая кафедра«Механика механизмов и машин» Заведующий кафедрой Шевченко Игорь Владимирович Организационная структура Московский ИВЦ
Организационная структура Московский ИВЦ День рождения Деда Мороза
День рождения Деда Мороза Поздравление с Новым годом
Поздравление с Новым годом Радиотехнические системы (РТС)
Радиотехнические системы (РТС) Презентация Microsoft PowerPoint [Автосохраненный]
Презентация Microsoft PowerPoint [Автосохраненный] Плюсы группы Т Плюс
Плюсы группы Т Плюс КВН – игра «В стране географов и географинь»
КВН – игра «В стране географов и географинь» Компьютерный кружок
Компьютерный кружок Изучение работы сварного соединения
Изучение работы сварного соединения  Осень… На улице холодно и сыро
Осень… На улице холодно и сыро Презентация на тему Познавательные способности
Презентация на тему Познавательные способности Башкирский государственный университет. Магистратура по социологии
Башкирский государственный университет. Магистратура по социологии Слово и время
Слово и время ИСПОЛЬЗОВАНИЕ МОБИЛЬНОГО КОМПЬЮТЕРНОГО КЛАССАВ УЧЕБНО-ВОСПИТАТЕЛЬНОМ ПРОЦЕССЕ МОУ СОШ 30
ИСПОЛЬЗОВАНИЕ МОБИЛЬНОГО КОМПЬЮТЕРНОГО КЛАССАВ УЧЕБНО-ВОСПИТАТЕЛЬНОМ ПРОЦЕССЕ МОУ СОШ 30 Презентация на тему Презентация "Буквы Уу Ээ"
Презентация на тему Презентация "Буквы Уу Ээ" Nature’s Sunshine Products
Nature’s Sunshine Products Православная молитва
Православная молитва ПСИХОЛОГИЧЕСКИЙ ВЕСТНИК
ПСИХОЛОГИЧЕСКИЙ ВЕСТНИК ИТОГИ РАБОТЫ ЗА 2011 ГОД
ИТОГИ РАБОТЫ ЗА 2011 ГОД Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании Северодвинск
Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании Северодвинск Орнамент
Орнамент Презентация на тему А нужен ли Калгон?
Презентация на тему А нужен ли Калгон?