Содержание
- 2. В стереометрии изучаются фигуры в пространстве, называемые телами. Наглядно тело надо представлять себе как часть пространства,
- 3. Поясним сказанное на примере знакомого вам куба. Куб есть выпуклый многогранник. Его поверхность состоит из шести
- 4. Простейшим многогранникам – призмам и пирамидам, которые будут основным объектом нашего изучения, - мы дадим такие
- 5. План урока: Понятие призмы и ее основные элементы Виды призм Площадь поверхности призмы Теорема о площади
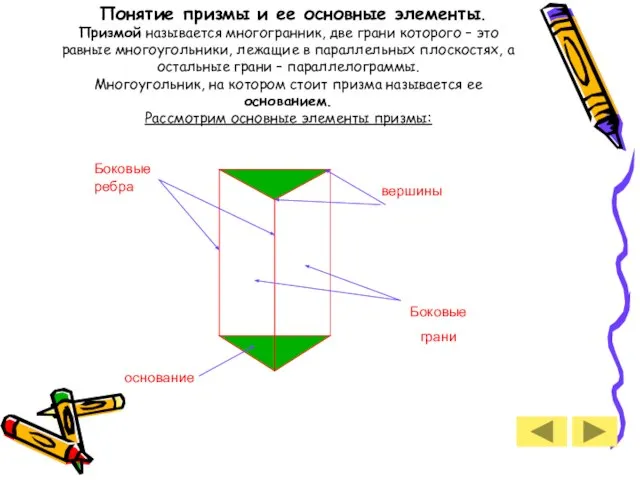
- 6. Понятие призмы и ее основные элементы. Призмой называется многогранник, две грани которого – это равные многоугольники,
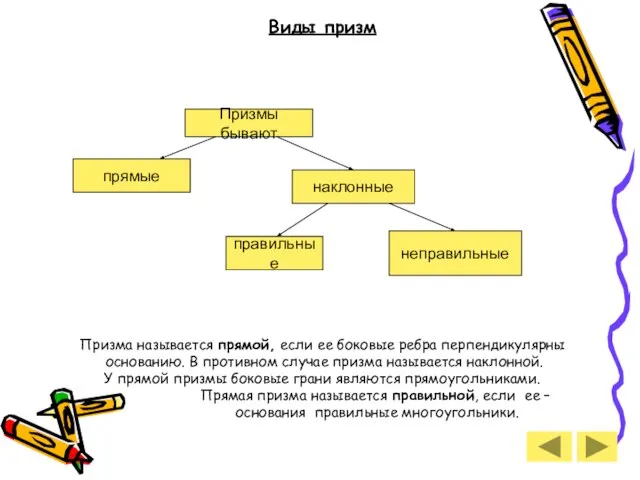
- 7. Виды призм Призма называется прямой, если ее боковые ребра перпендикулярны основанию. В противном случае призма называется
- 8. Площадь поверхности призмы Теорема о площади боковой поверхности призмы Боковой поверхностью призмы называется сумма площадей ее
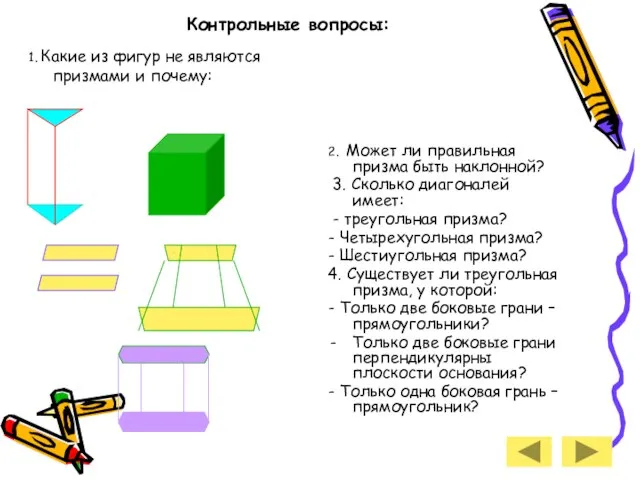
- 9. Контрольные вопросы: 1. Какие из фигур не являются призмами и почему: 2. Может ли правильная призма
- 10. Урок 3-4 План урока: Понятие параллелепипеда, его виды и элементы Свойства параллелепипеда Виды параллелепипедов Контрольные вопросы
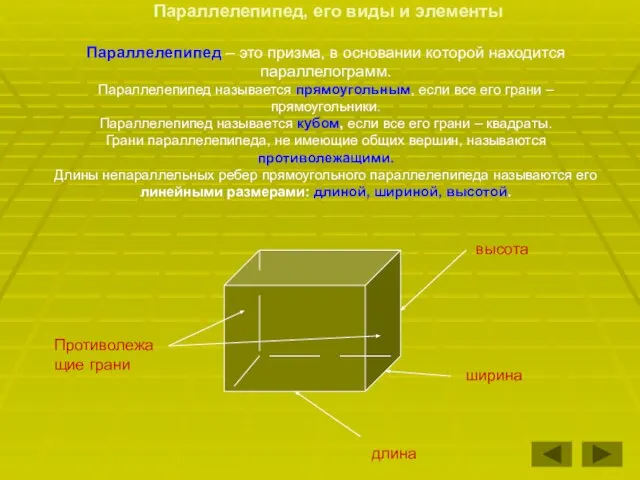
- 11. Параллелепипед, его виды и элементы Параллелепипед – это призма, в основании которой находится параллелограмм. Параллелепипед называется
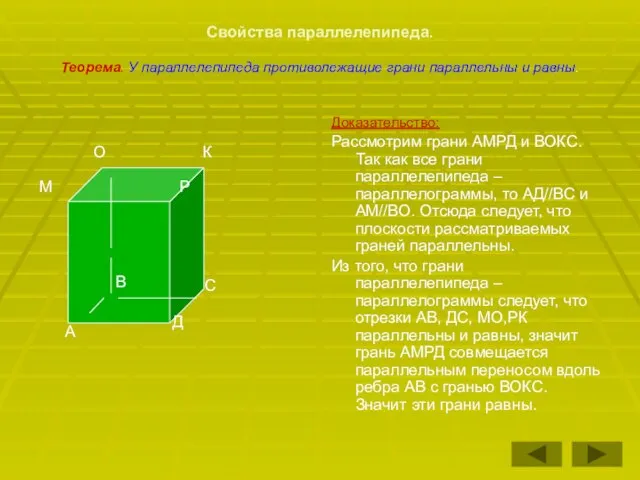
- 12. Свойства параллелепипеда. Теорема. У параллелепипеда противолежащие грани параллельны и равны. Доказательство: Рассмотрим грани АМРД и ВОКС.
- 13. Свойства параллелепипеда. Теорема. У параллелепипеда диагонали пересекаются в одной точке и точкой пересечения делятся пополам. Доказательство:
- 14. Свойства параллелепипеда. Теорема. В прямоугольном параллелепипеде квадрат любой его диагонали равен сумме квадратов трех его измерений..
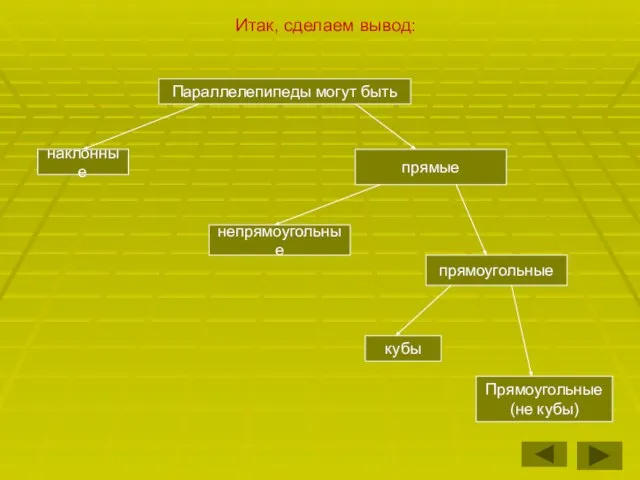
- 15. Итак, сделаем вывод: Параллелепипеды могут быть прямые прямоугольные наклонные непрямоугольные кубы Прямоугольные (не кубы)
- 16. А теперь ответьте на Контрольные вопросы: Верно ли утверждение: - все грани прямоугольного параллелепипеда – прямоугольники;
- 17. Урок 5-6 План урока: Понятие пирамиды и ее основные элементы. Площадь поверхности пирамиды. Теорема о площади
- 18. Понятие пирамиды и ее основные элементы Пирамидой называется многогранник, в основании которого находится многоугольник, а остальные
- 19. Площадь поверхности пирамиды. Теорема о площади боковой поверхности правильной пирамиды. Боковой поверхностью пирамиды называется сумма площадей
- 20. Усеченная пирамида и ее элементы. Усеченной называется пирамида, полученная из обычной пирамиды путем отсечения ее вершины
- 22. Скачать презентацию













 совместно с Театром праздника «Солнечный зайчик»
совместно с Театром праздника «Солнечный зайчик» ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс
ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс Презентация на тему Врожденные и приобретенные программы поведения
Презентация на тему Врожденные и приобретенные программы поведения Презентация
Презентация ПРОЕКТНАЯ РАБОТА
ПРОЕКТНАЯ РАБОТА к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич
к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич Культура Руси в 10 – 13 веках
Культура Руси в 10 – 13 веках Болгария в 20-30-е годы
Болгария в 20-30-е годы Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя
Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя Приготовление завтрака
Приготовление завтрака «Инвестиционная политика муниципального образования на современном этапе»02.02.2012
«Инвестиционная политика муниципального образования на современном этапе»02.02.2012 Работа академии по направлению научно-технического творчества молодежи
Работа академии по направлению научно-технического творчества молодежи «Трудные» дети и их проблемы.
«Трудные» дети и их проблемы. Приемы расположения к себе. Самопрезентация
Приемы расположения к себе. Самопрезентация Автохимия. Завод автохимии
Автохимия. Завод автохимии Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года
Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года Евангелие от Матфея
Евангелие от Матфея Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов
Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов Аварийная аптечка для первой медицинской помощи
Аварийная аптечка для первой медицинской помощи Власть. Сила. Лекция 2
Власть. Сила. Лекция 2 Вітражі та шпроси
Вітражі та шпроси Моя будущая профессия - бухгалтер
Моя будущая профессия - бухгалтер Олимпиада үрләренә - баскычлап
Олимпиада үрләренә - баскычлап Общероссийские антидопинговые правила
Общероссийские антидопинговые правила Проектирование транспортно-грузовых комплексов
Проектирование транспортно-грузовых комплексов Определение размеров молекул октана
Определение размеров молекул октана Такси Лось
Такси Лось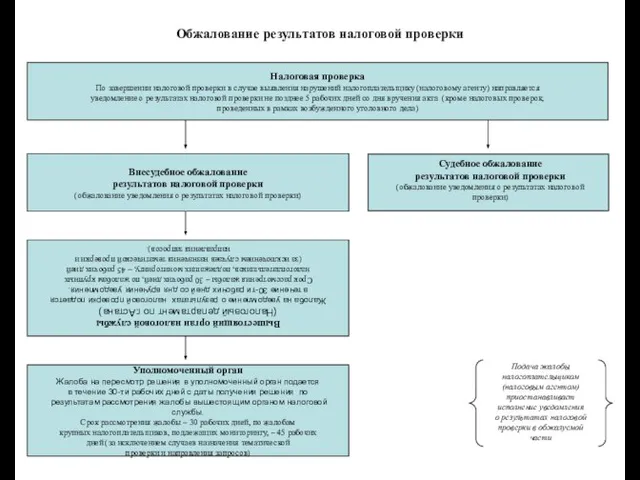 Обжалование результатов налоговой проверки
Обжалование результатов налоговой проверки