Содержание
- 2. Многогранник — поверхность, составленная из многоугольников и ограничивающих некоторое геометрическое тело. Многогранники бывают выпуклыми и невыпуклыми
- 3. Двойственный многогранник Многогранник, двойственный (или дуальный) к заданному многограннику — многогранник, у которого каждой грани исходного
- 4. Изгибаемый многогранник Многогранник (точнее — многогранная поверхность) называется изгиба́емым, если его пространственную форму можно изменить такой
- 5. Полуправильный многогранник Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными,
- 7. многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон
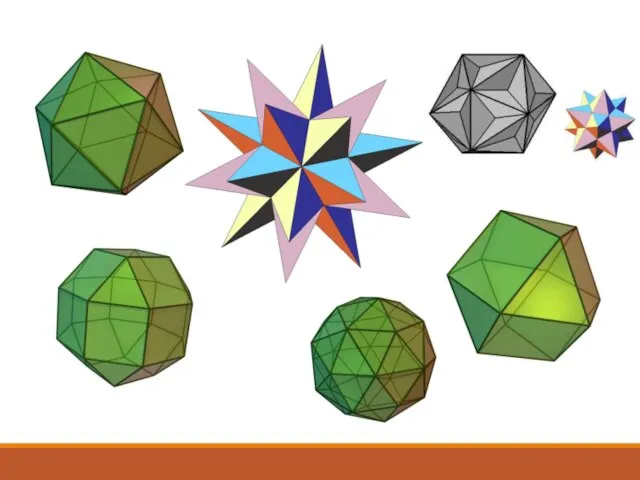
- 8. Существует 5 типов правильных многогранников Правильный додекаэдр Правильный икосаэдр Правильный гексаэдр Правильный тетраэдр Правильный октаэдр
- 9. Тетраэдр Тетра́эдр (греч. τετραεδρον — четырёхгранник) — многогранник с четырьмя треугольными гранями, в каждой из вершин
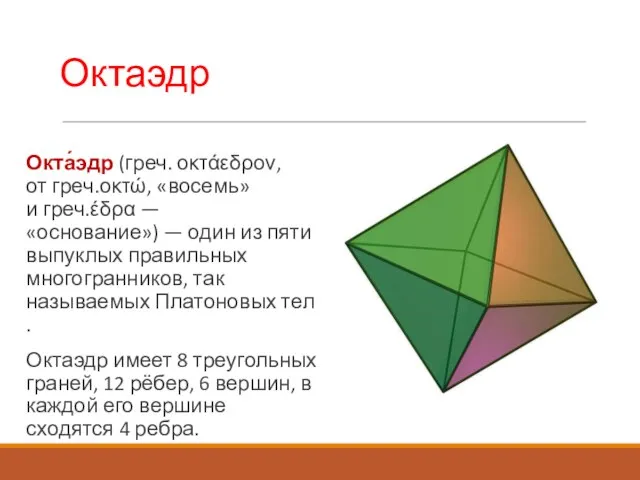
- 10. Октаэдр Окта́эдр (греч. οκτάεδρον, от греч.οκτώ, «восемь» и греч.έδρα — «основание») — один из пяти выпуклых
- 11. Гексаэдр (куб) Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный
- 12. Икосаэдр Икоса́эдр (от греч. εικοσάς — двадцать; -εδρον — грань, лицо, основание) — правильный выпуклый многогранник,
- 13. Додекаэдр Додека́эдр (от греч. δώδεκα — двенадцать и εδρον — грань),двенадцатигранник —правильный многогранник, составленный из двенадцати
- 14. Историческая справка О существовании всего лишь пяти правильных многогранников знали еще в Древней Греции. Великий древнегреческий
- 15. Леонард Эйлер (1707-1783г.г.) Эйлер - швейцарский математик и механик, академик Петербургской Академии Наук, автор огромного количества
- 16. По горизонтали: 2. Правильный шестигранник. 4. Плоские многоугольники, из которых состоит поверхность многогранника. 5. Высота боковой
- 17. Применение в кристаллографии Тела Платона нашли широкое применение в кристаллографии, так как многие кристаллы имеют форму
- 18. Поваренная соль состоит из кристаллов в форме куба Скелет одноклеточного организма феодарии представляет собой икосаэдр. Минерал
- 19. Многогранники в архитектуре Еги́петские пирами́ды —Пирамиды представляют собой огромные каменные сооружения пирамидальной формы, использовавшиеся в качестве
- 20. Фаросский маяк Александри́йский мая́к (Фа́росский маяк) — маяк, построенный в lll веке до н.э. на острове
- 21. Башни Смоленской крепости
- 22. В искусстве. Альбрехт Дюрер «меланхолия» «Меланхолия» — резцовая гравюра на меди немецкого художника Альбрехта Дюрера, законченная
- 24. Скачать презентацию



















 Маркетинг территории в России: возможности и технологии
Маркетинг территории в России: возможности и технологии Презентация на тему Физиология почки
Презентация на тему Физиология почки  Практика распределенной разработки в Open-Source проектах.
Практика распределенной разработки в Open-Source проектах. Таможенные операции и таможенные процедуры
Таможенные операции и таможенные процедуры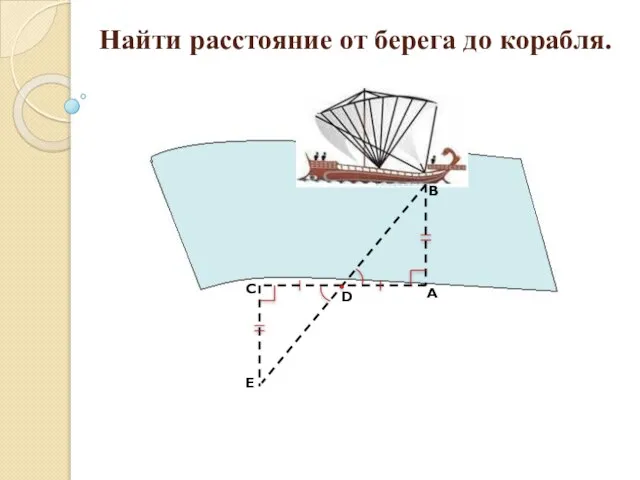 Найти расстояние от берега до корабля.
Найти расстояние от берега до корабля. Взаимодействие пути и подвижного состава
Взаимодействие пути и подвижного состава Process Analysis
Process Analysis Уральский экономический район
Уральский экономический район ТЕХНИЧЕСКОЕ ЗАДАНИЕ
ТЕХНИЧЕСКОЕ ЗАДАНИЕ Праздник Пасхи
Праздник Пасхи Город творческой интеллигенции
Город творческой интеллигенции Доклад Партнерские связи Лешуконского, Мезенского и Пинежского районов как способ развития территории
Доклад Партнерские связи Лешуконского, Мезенского и Пинежского районов как способ развития территории Географические названия на буквы Н и К
Географические названия на буквы Н и К Труд и семья с точки зрения закона
Труд и семья с точки зрения закона Проблемы, возникающие при регулировании тарифов методом доходности инвестированного капитала
Проблемы, возникающие при регулировании тарифов методом доходности инвестированного капитала ЭЛЕКТРОСНАБЖЕНИЕ_Ч1(заочн)
ЭЛЕКТРОСНАБЖЕНИЕ_Ч1(заочн) Малинова О.Ю. Конструирование «общепринятого»: использование прошлого для легитимации политического курса (на примере анализа е
Малинова О.Ю. Конструирование «общепринятого»: использование прошлого для легитимации политического курса (на примере анализа е Семейный эколого-туристический клуб
Семейный эколого-туристический клуб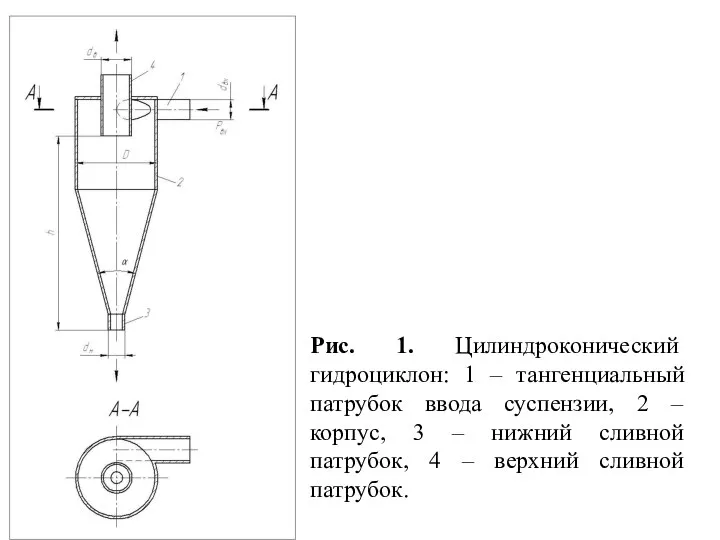 Гидромеханические установки. Цилиндроконический гидроциклон. (Лекция 5)
Гидромеханические установки. Цилиндроконический гидроциклон. (Лекция 5) Виды печатных машинок
Виды печатных машинок Этикет 2 класс
Этикет 2 класс Gene Expression Systems
Gene Expression Systems Недаром помнит вся Россия про день Бородина! 6 класс
Недаром помнит вся Россия про день Бородина! 6 класс ШЕЙНГАУЗ АЛЕКСАНДР СОЛОМОНОВИЧ заведующий отделом института экономических исследований ДВО РАН, д.с-х.н., профессор
ШЕЙНГАУЗ АЛЕКСАНДР СОЛОМОНОВИЧ заведующий отделом института экономических исследований ДВО РАН, д.с-х.н., профессор Возможности Emerson по Продукции и Сервису $ 22,6 Миллиарда - доходы более чем 60 подразделений
Возможности Emerson по Продукции и Сервису $ 22,6 Миллиарда - доходы более чем 60 подразделений Презентация на тему Насекомые вредители поля и огорода
Презентация на тему Насекомые вредители поля и огорода  Русь в XIII – XV веках Монгольское нашествие на Русь
Русь в XIII – XV веках Монгольское нашествие на Русь Мой выбор - терапия
Мой выбор - терапия