Статистические методы в QSAR

Затронутые темы
Многомерный анализ данных
Понятие о дескрипторном пространстве, химическом расстоянии
Понятие о дискриминантном и кластерном анализах
Метрика дескрипторного пространства. Коллинеарные и ортогональные дескрипторы
Латентные дескрипторы, оценки (scores) и нагрузки (loading)
Понятие о факторном анализе и методе главных компонент (PCA)
Метод частичных наименьших квадратов (PLS)

Многомерный анализ данных
Традиционные регрессионные процедуры - число столбцов в матрицах дескрипторов X относительно невелико, и между ними отсутствуют линейные зависимости
Процедуры многомерного анализа данных могут работать с матрицами дескрипторов X, содержащими большое количество столбцов, многие из которых линейно-зависимы

Центрирование данных для многомерного анализа
, где
, где

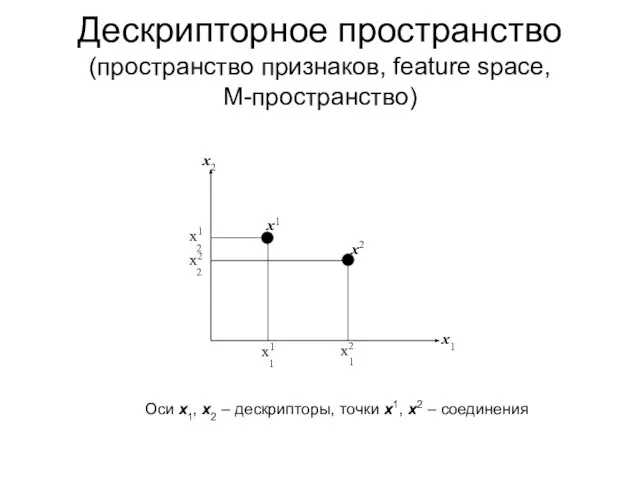
Дескрипторное пространство
(пространство признаков, feature space,
M-пространство)
Оси x1, x2 – дескрипторы, точки x1, x2 – соединения

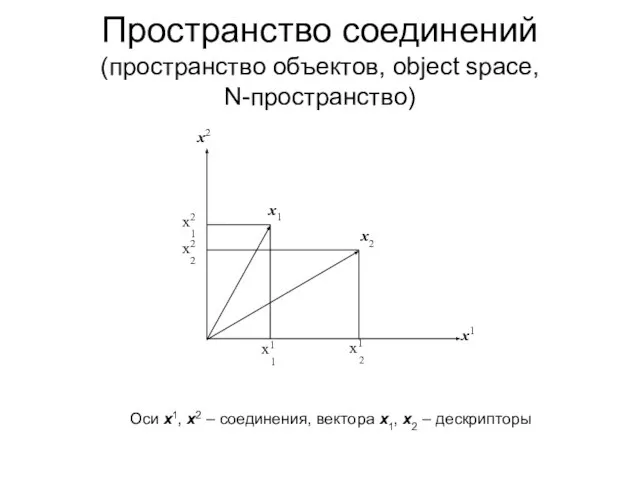
Пространство соединений (пространство объектов, object space,
N-пространство)
Оси x1, x2 – соединения, вектора x1, x2 – дескрипторы

Метрика дескрипторного пространства
(химическое расстояние)
Эвклидово расстояние
Манхэттоновское расстояние
Метрика Минковского

Принцип сходства
(Similarity Principle)
Постулируется принцип: структурно близкие химические соединения обладают сходными свойствами
Предполагается, что всегда можно найти такой набор дескрипторов и такую метрику дескрипторного пространства, чтобы этот принцип выполнялся

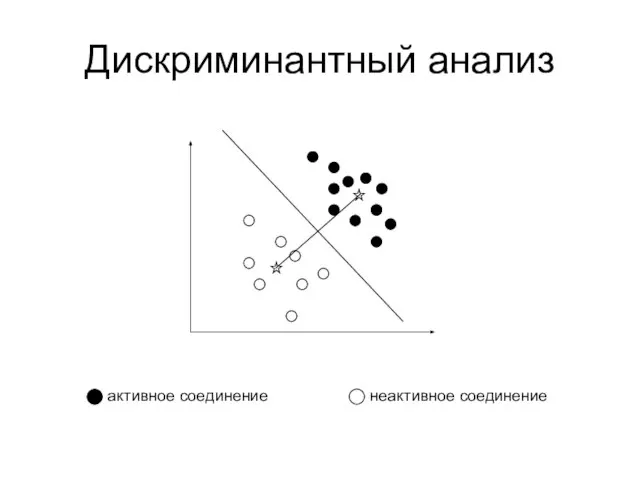
Дискриминантный анализ
активное соединение
неактивное соединение

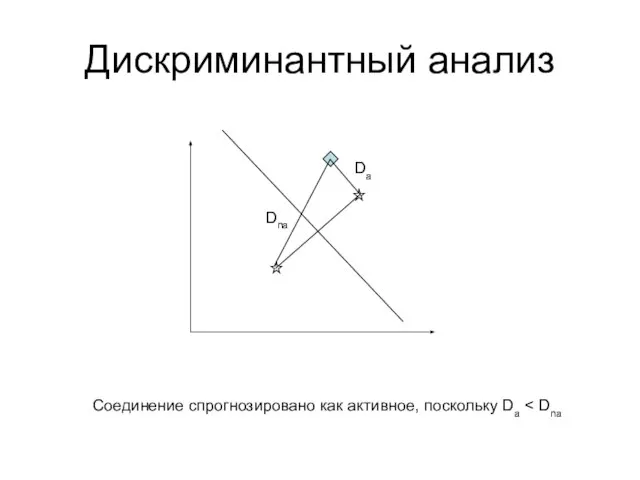
Дискриминантный анализ
Da
Dna
Соединение спрогнозировано как активное, поскольку Da < Dna

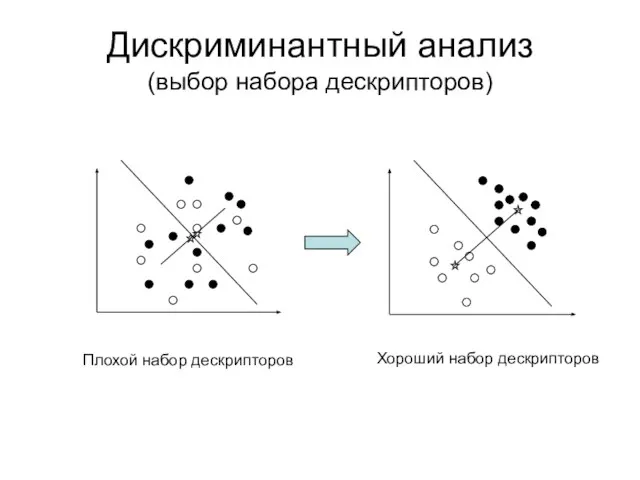
Дискриминантный анализ
(выбор набора дескрипторов)
Плохой набор дескрипторов
Хороший набор дескрипторов

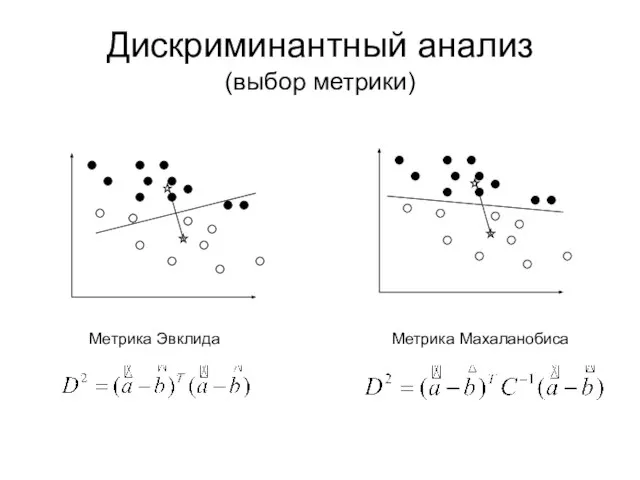
Дискриминантный анализ
(выбор метрики)
Метрика Эвклида
Метрика Махаланобиса

Метод ближайших соседей
(kNN – k Nearest Neighbours)
Соединение прогнозируется как активное, поскольку Da < Dna

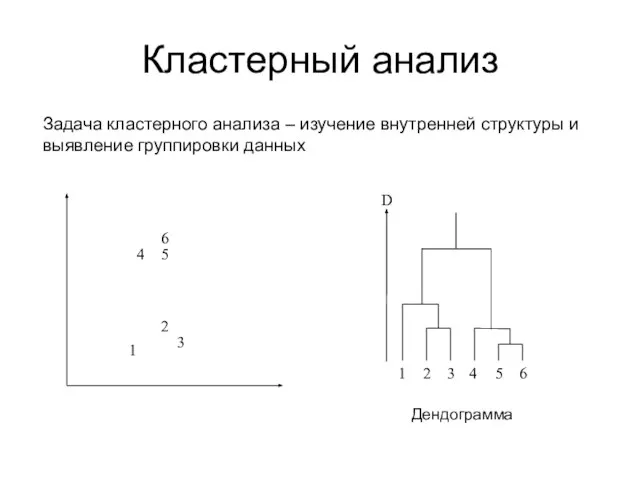
Кластерный анализ
Задача кластерного анализа – изучение внутренней структуры и выявление группировки данных
Дендограмма

Свойства пространства соединений
- скалярное произведение векторов
- косинус угла между векторами
- ковариация
- коэффициент корреляции

Свойства пространства соединений
Коллинеарные вектора – дескрипторы статистически эквивалентны
Перпендикулярные вектора – дескрипторы линейно независимы

Латентные переменные
Одной из главных задач многомерного анализа данных является выявление таких комбинаций исходных переменных (дескрипторов), которые бы позволили эффективно решать актуальные задачи:
Описать данные наименьшим числом переменных (факторный анализ)
Добиться максимального разделения классов (факторный дискриминантных анализ)
Построить регрессионную модель с наилучшей прогнозирующей способностью (метод частичный наименьших квадратов)
и т.д.
Подобные комбинации исходных переменных называются латентными переменными (скрытыми факторами, оценками)

Линейные латентные переменные
Матрица оценок (scores)
Матрица нагрузок (loading)
Вектора s обычно берутся ортогональными,
т.е. латентные переменные линейно независимы

Метод главных компонент
(PCA – Principal Component Analysis)
Цель метода главных компонент – описание данных минимально возможным количеством латентных переменных
- SVD (Singular Value Decomposition) разложение
Матрица сингулярных значений

Метод главных компонент
(PCA – Principal Component Analysis)
C = XTX – матрица ковариаций

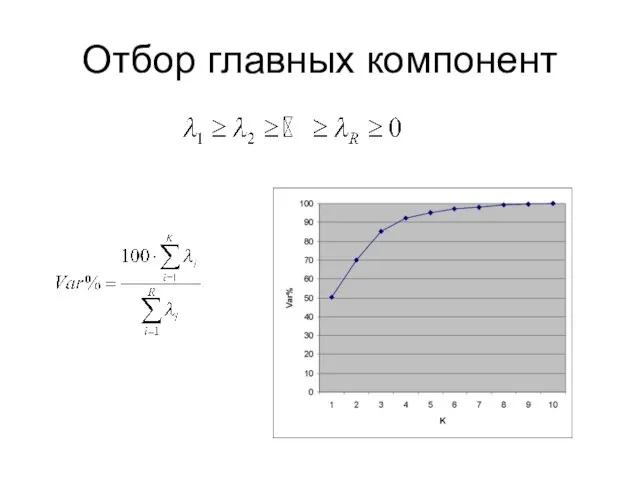
Отбор главных компонент

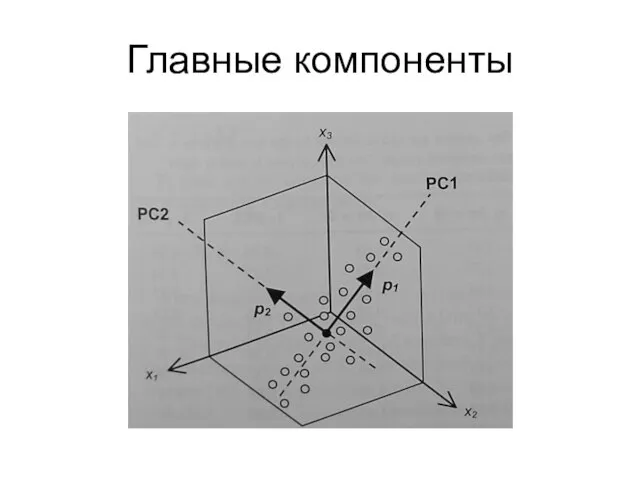
Главные компоненты

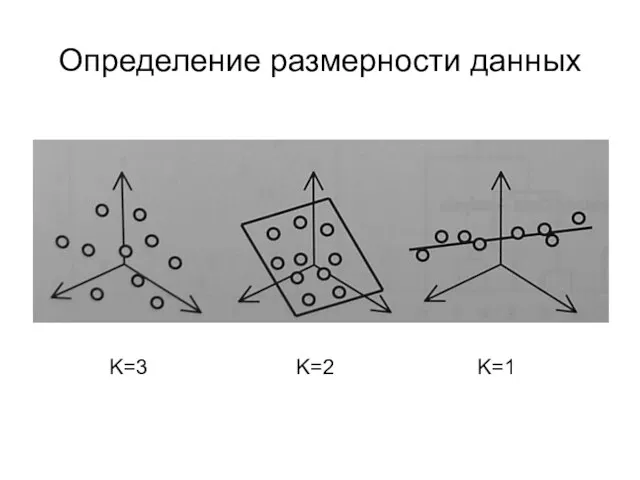
Определение размерности данных
K=3
K=2
K=1

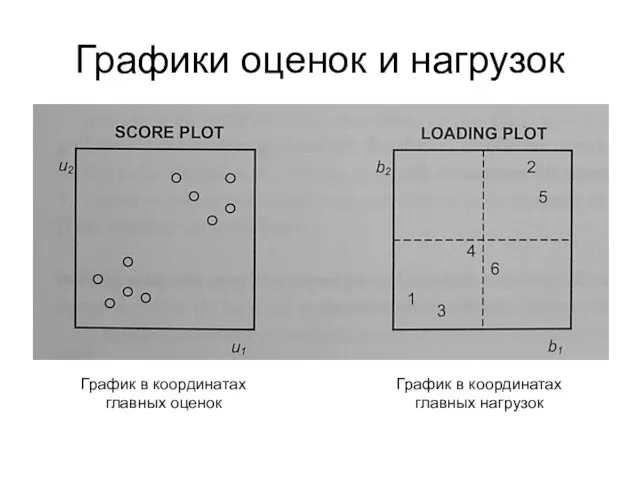
Графики оценок и нагрузок
График в координатах главных оценок
График в координатах главных нагрузок

Резюме метода главных компонент
Вычисляется матрица ковариаций
Находятся ее собственные вектора и собственные значения
Отбираются латентные переменные, соответствующие двум наибольшим собственным значениям
Строятся 2-мерные графики оценок и нагрузок

Факторный анализ
Определяется число латентных переменных, необходимых для воспроизведения данных с заданной точностью
Путем вращения векторов исходных латентных переменных ищутся легко интерпретируемые варианты

Факторный (канонический) дискриминантный анализ
Ищутся латентные переменные, позволяющие получить наилучшее разделение классов путем максимизации отношения межгрупповой к общей дисперсии

Метод частичных наименьших квадратов (PLS – Partial Least Squares)
В методе частичных наименьших квадратов ищется набор латентных переменных, позволяющий получить регрессионную модель с наилучшей прогнозирующей способностью

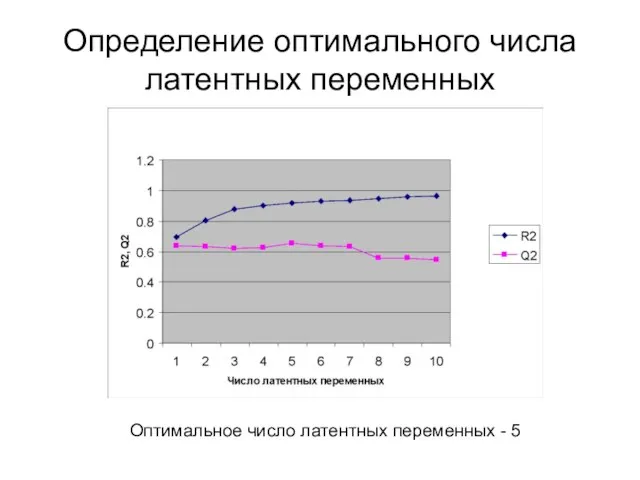
Определение оптимального числа латентных переменных
Оптимальное число латентных переменных - 5