Содержание
- 2. Модели ценообразования на финансовом рынке 1. Модель оценки капитальных активов (CAPM - Capital Asset Pricing Model)
- 3. Предположения в отношении рынка в целом отсутствуют налоги и затраты на совершение сделок; вся информация о
- 4. 1. Активы не бесконечно делимы, информация среди участников рынка распространяется неравномерно, существуют операционные издержки и ограничения
- 5. Рыночный портфель В условиях, когда выполняются предположения модели САРМ, все инвесторы стремятся сформировать одинаковый по структуре
- 7. Анализ (САМР) Модель САМР описывает зависимость между рыночным риском и требуемой доходностью при определенных условиях (инвесторы
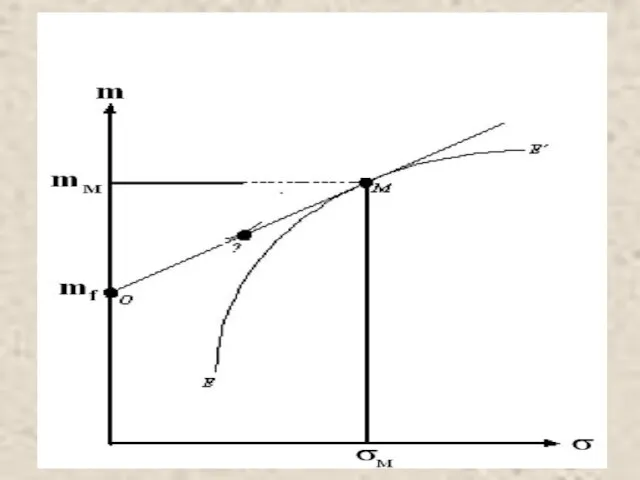
- 8. mi - ожидаемый доход на ценную бумагу i при равновесии рынка; mf - ставка дохода на
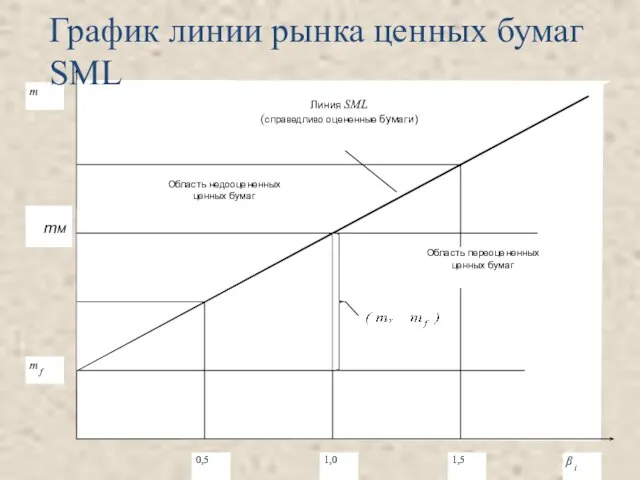
- 9. График линии рынка ценных бумаг SML mM
- 10. Анализ SML В соответствии с моделью САРМ, в условиях равновесия доходность всех ценных бумах должна располагаться
- 11. Линия SML
- 12. Рыночный риск и индивидуальный риск
- 13. Уравнение характеристической прямой для i-го актива. Уравнение характеристической кривой фактическая доходность ЦБ Величина αi может быть
- 14. Коэффициент альфа финансового актива Разница между фактически ожидаемой доходностью ценной бумаги и равновесной ставкой доходности называют
- 15. Рыночный риск и индивидуальный риск
- 17. Значение бета - коэффициента Коэффициент регрессии β служит количественным измерителем систематического риска, не поддающегося диверсификации. Ценная
- 18. Безрисковая ставка доходности Практически, в качестве безрисковой ставки выбирают, как правило, ставку доходности по краткосрочным (от
- 19. Рыночная доходность Один из наиболее сложных вопросов - расчет рыночной доходности. Как правило, для этой цели
- 20. Расчет ожидаемой доходности и стандартного отклонения Наиболее простой, но чаще всего используемый на практике метод -
- 21. Выводы Модель CAPM представляет собой идеальную модель рынка капиталов, которая основывается на предположениях портфельной теории и
- 22. Риск, связанный с инвестициями в каждую ценную бумагу можно разделить на две составляющие - рыночный (системный)
- 23. Коэффициент бета представляет собой коэффициент ковариации доходности финансового актива и доходности рыночного портфеля, деленный на дисперсию
- 25. Скачать презентацию








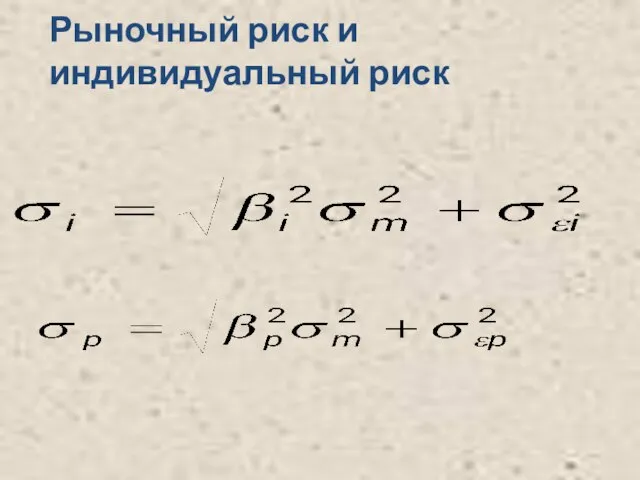


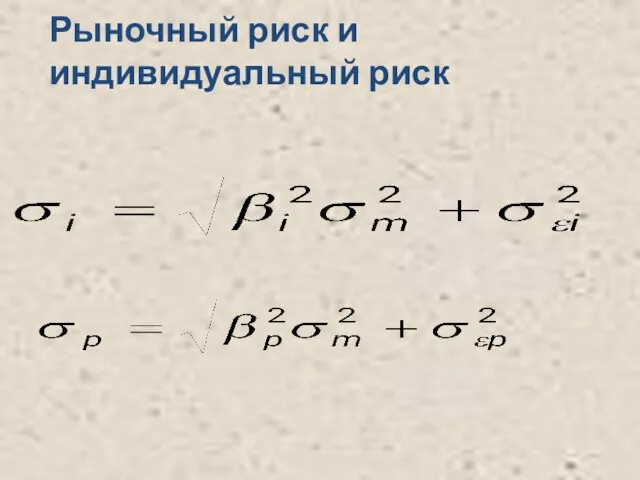








 Математическая игра«Счастливый случай» (9-10 класс)
Математическая игра«Счастливый случай» (9-10 класс) Apostel Paulus/ Paulus von Tarsus
Apostel Paulus/ Paulus von Tarsus Животные в космосе
Животные в космосе Балет
Балет кп.ppt
кп.ppt Договор возмездного оказания услуг Выполнил: студент IV курса группа ДС-04 Шацких Алексей
Договор возмездного оказания услуг Выполнил: студент IV курса группа ДС-04 Шацких Алексей «Единое образовательное пространство ГОУ СОШ №126: проблемы создания и перспективы развития»
«Единое образовательное пространство ГОУ СОШ №126: проблемы создания и перспективы развития» Числа 0 - 10
Числа 0 - 10 О нашем классе
О нашем классе Экологизация школьного курса окружающего мира
Экологизация школьного курса окружающего мира Модернизация агрегатного участка ремонтной мастерской в КФХ ИП Латыпов Ф.Т
Модернизация агрегатного участка ремонтной мастерской в КФХ ИП Латыпов Ф.Т Курсовая работа Adobe Illustrator
Курсовая работа Adobe Illustrator Образ свах в произведениях русских писателей Н.В. Гоголя «Женитьба», Н.С. Лескова «Воительница», А.Н. Островского «Женитьба Бальзам
Образ свах в произведениях русских писателей Н.В. Гоголя «Женитьба», Н.С. Лескова «Воительница», А.Н. Островского «Женитьба Бальзам Инстант порукеInstant messaging
Инстант порукеInstant messaging Технологии деловой переписки и телефонных переговоров с гостем для эффективного ведения гостиничного бизнеса
Технологии деловой переписки и телефонных переговоров с гостем для эффективного ведения гостиничного бизнеса Савина Татьяна Анатольевна – учитель географии высшей категории
Савина Татьяна Анатольевна – учитель географии высшей категории Анализ сферы профилактики правонарушений
Анализ сферы профилактики правонарушений Презентация на тему ОБ ИТОГАХ ВСЕРОССИЙСКОЙ ПЕРЕПИСИ НАСЕЛЕНИЯ 2010 ГОДА
Презентация на тему ОБ ИТОГАХ ВСЕРОССИЙСКОЙ ПЕРЕПИСИ НАСЕЛЕНИЯ 2010 ГОДА  Прочитайте отрывок из труда Н.И. Костомарова об отношении к реформам населения в XVII в.? «…а мы от разумных людей слыхали: которая зе
Прочитайте отрывок из труда Н.И. Костомарова об отношении к реформам населения в XVII в.? «…а мы от разумных людей слыхали: которая зе Лекции 6 - 7
Лекции 6 - 7 1.Организационный момент.
1.Организационный момент. Александр Дюма. Творчество
Александр Дюма. Творчество Как сделать вычислительную инфраструктуру для большого кластера
Как сделать вычислительную инфраструктуру для большого кластера Презентация на тему Тренируем память. Виды памяти. Приемы запоминания
Презентация на тему Тренируем память. Виды памяти. Приемы запоминания Часть 1Современные концепции воспитания
Часть 1Современные концепции воспитания Анализ конкурентоспособности сложной технической продукции
Анализ конкурентоспособности сложной технической продукции Инклюзивное образование
Инклюзивное образование Наша бібліотека
Наша бібліотека