Слайд 2Задача.
Построить математическую модель физического процесса — движения тела, брошенного под углом к

горизонту.
Выяснить зависимость расстояния и времени полета тела от угла броска и начальной скорости.
Угол броска и начальная скорость являются главными факторами процесса моделирования.
Слайд 3 Решение.
При расчетах будем использовать следующие допущения:
начало системы координат расположено в

точке бросания;
тело движется вблизи поверхности Земли, т. е. ускорение свободного падения постоянно и равно 9,81 м/с²;
сопротивление воздуха не учитывается, поэтому движение по горизонтали равномерное.
Слайд 4Vo — начальная скорость (м/с),
α — угол бросания (радиан),
L —
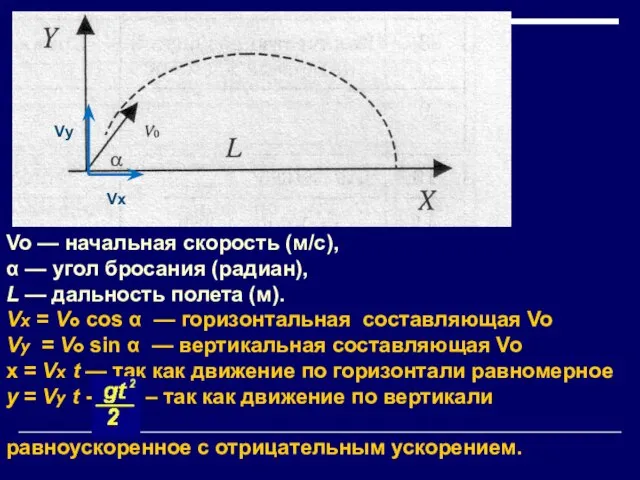
дальность полета (м).
Vx = Vo cos α — горизонтальная составляющая Vo
Vy = Vo sin α — вертикальная составляющая Vo
х = Vx t — так как движение по горизонтали равномерное
у = Vy t - – так как движение по вертикали
равноускоренное с отрицательным ускорением.
Слайд 5Искомым в этой задаче будет то
значение х = L, при котором

у = 0.
(1) L = Vx t — дальность полета,
(2) 0 = Vy t – — точка падения,
(3) Vx = Vo cos α — горизонтальная проекция вектора начальной скорости,
(4) Vy = Vo sin α — вертикальная проекция вектора начальной скорости,
g = 9,81 — ускорение свободного падения,
Vo > 0
0 < α < .
Слайд 6Подставляем в формулу (2) значение Vy из формулы (4).
Получаем уравнение:
(5)
Найдем

из формул (1) и (3) выражение для t:
Слайд 7Подставив значение t в уравнение (5), получаем решение:

Слайд 8или
Отсюда дальность полета равна:
т. е. зависит от начальной скорости и угла наклона.

Слайд 9Проведем исследование полученной математической модели, чтобы выяснить, как зависит дальность полета от

угла броска.
Зададим количественные величины для моделирования:
Vo=60 м/с
α = 10 …80 град.
Δα = 10 град.
g = 9,81
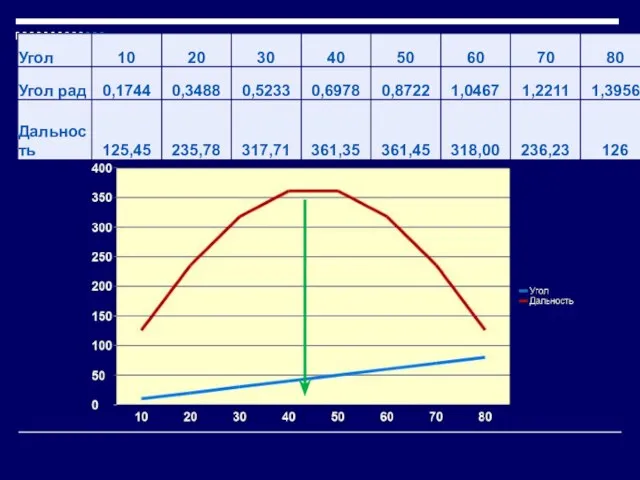
Результаты моделирования приведем в таблице и на графике.
Слайд 11Выводы:
С увеличением угла бросания от 15 до 45° при постоянной начальной скорости

полета дальность полета увеличивается.
С увеличением угла бросания от 45 до 90° при постоянной начальной скорости полета дальность полета уменьшается.
Слайд 122. Выяснить, как зависит на Луне дальность полета от угла броска (g

= 1,63 м/с²)










 Презентация на тему Алгебра и логика высказываний
Презентация на тему Алгебра и логика высказываний Заболевание височно-нижнечелюстного сустава
Заболевание височно-нижнечелюстного сустава  Конфликтный треугольник: семья-ребенок-образовательное учреждение. Детская агрессия
Конфликтный треугольник: семья-ребенок-образовательное учреждение. Детская агрессия кольцово
кольцово Проблемы преемственности начального и основного (общего) образования
Проблемы преемственности начального и основного (общего) образования Проектная деятельность
Проектная деятельность Власть. Структурная и ситуационная власть
Власть. Структурная и ситуационная власть Свечникова В.В. правоведение тема 2 презентация
Свечникова В.В. правоведение тема 2 презентация Майолика. Гутные изделия. Ковка
Майолика. Гутные изделия. Ковка Saint Petersburg state University
Saint Petersburg state University 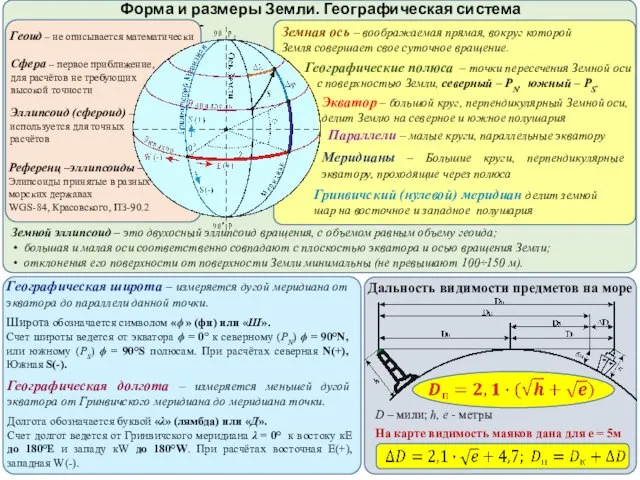 Форма и размеры Земли
Форма и размеры Земли Поздравление крестной жениха
Поздравление крестной жениха Гендерные аспекты образования и рынка труда
Гендерные аспекты образования и рынка труда Геометрия на службе у архитектуры
Геометрия на службе у архитектуры Психология двигательно-волевой сферы психической деятельности
Психология двигательно-волевой сферы психической деятельности Команда звёздочки
Команда звёздочки История семейного образования в СанктПетербурге
История семейного образования в СанктПетербурге Русский пейзаж в поэзии и живописи
Русский пейзаж в поэзии и живописи Физическая культура в период самоизоляции студентов педагогического вуза
Физическая культура в период самоизоляции студентов педагогического вуза Заповедники России
Заповедники России Презентация на тему Прощание с 1 классом
Презентация на тему Прощание с 1 классом Клёш и фалды
Клёш и фалды Быть нормальным
Быть нормальным Основные формы рельефа Алтайского края
Основные формы рельефа Алтайского края  Проект: Комплексное сопровождение покупки страховой компании
Проект: Комплексное сопровождение покупки страховой компании Сделка. Предпринимательская деятельность
Сделка. Предпринимательская деятельность русский язык - язык международного общения
русский язык - язык международного общения Условия признания и исполнения иностранных судебных решений
Условия признания и исполнения иностранных судебных решений