Моделирование физических процессов

Задача.
Построить математическую модель физического процесса — движения тела, брошенного под углом к горизонту.
Выяснить зависимость расстояния и времени полета тела от угла броска и начальной скорости.
Угол броска и начальная скорость являются главными факторами процесса моделирования.

Решение.
Постановка задачи.
При расчетах будем использовать следующие допущения:
начало системы координат расположено в точке бросания;
тело движется вблизи поверхности Земли, т. е. ускорение свободного падения постоянно и равно 9,81 м/с²;
сопротивление воздуха не учитывается, поэтому движение по горизонтали равномерное.

Пусть
Vo — начальная скорость (м/с),
α — угол бросания (радиан),
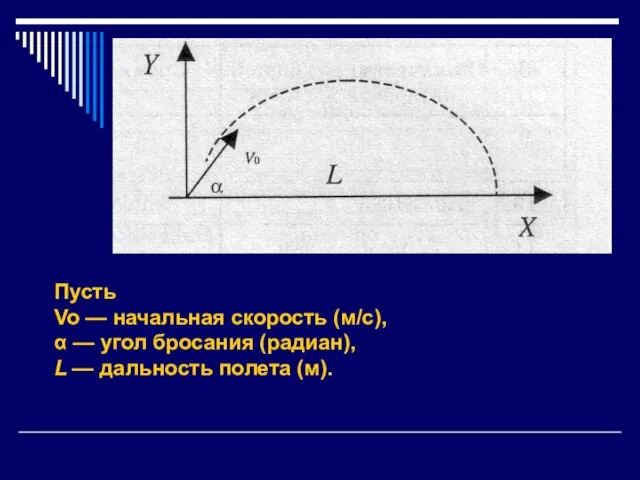
L — дальность полета (м).

Движение тела, брошенного под углом к горизонту, описывается следующими формулами:
Vx = Vo cos α — горизонтальная составляющая начальной скорости,
Vy = Vx sin α — вертикальная составляющая начальной скорости,
х = Vx t — так как движение по горизонтали равномерное,

у = Vy t - – так как движение по
вертикали равноускоренное с
отрицательным ускорением.
Искомым в этой задаче будет то
значение х = L, при котором у = 0.

Математическая модель.
Дано:
Vo — начальная скорость (м/с),
α — угол бросания (радиан).
Найти:
L — дальность полета (м).

Связь:
(1) L = Vx t - — дальность полета,
(2) 0 = Vy t – — точка падения,
(3) Vx = Vo cos α — горизонтальная проекция вектора начальной скорости,
(4) Vy = Vo sin α — вертикальная проекция вектора начальной скорости,
g = 9,81 — ускорение свободного падения,
Vo > 0
0 < α < .

Подставляем в формулу (2)
значение Vy из формулы (4).
Получаем уравнение:
(5)

Чтобы решить это уравнение, найдем из формул (1) и (3) выражение для t:

Подставив это значение в уравнение (5), получаем решение:

или
Отсюда дальность полета равна:
т. е. зависит от начальной скорости и угла наклона.

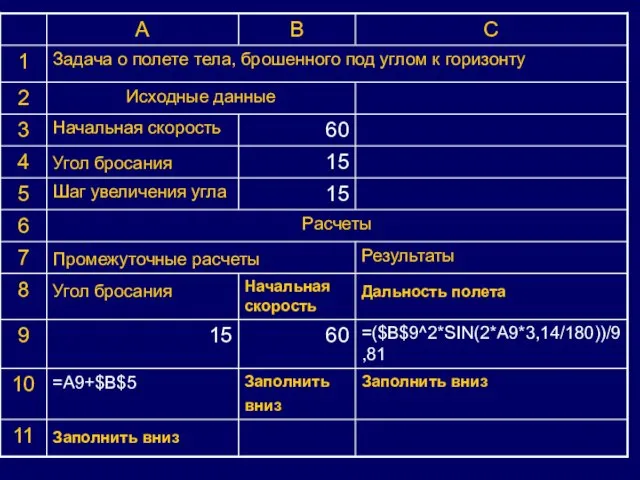
Компьютерный эксперимент.
I. Выяснить, как зависит дальность
полета от угла броска.
(Используем Excel)
В формульном виде:

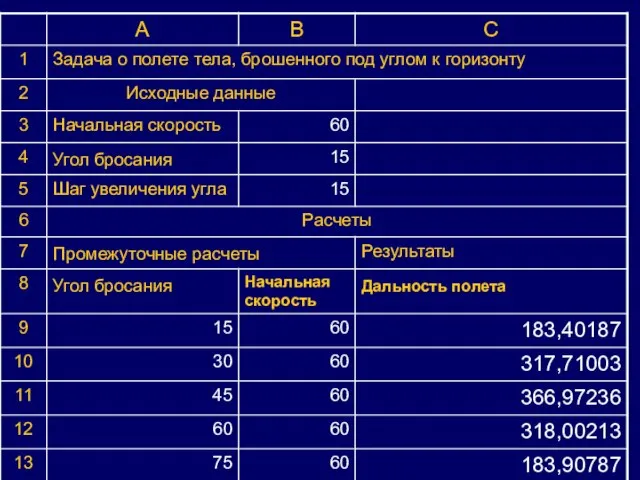
Делаем выводы:
С увеличением угла бросания от 15 до 45° при постоянной начальной скорости полета дальность полета увеличивается.
С увеличением угла бросания от 45 до 90° при постоянной начальной скорости полета дальность полета уменьшается.

2. Выяснить, как зависит на Луне дальность полета от угла броска (g = 1,63 м/с²)