Моделирование объектов и систем

1.1. Моделирование объекта
Решение задачи, выполнение проекта начинается с постановки задачи и ее описания. Описание необходимо для понимания деталей, для согласования с заказчиком исходных данных, понимания его требований.
Моделью называется описание изучаемого объекта, явления, процесса (далее просто объекта) некоторым способом с целью его изучения.
Иногда моделью называют упрощенную копию (?) объекта.

Моделирование объекта
Модель всегда описывает объект не полностью, не учитывает несущественные для исследования детали.
Если объект описан простым разговорным языком, без описания технических деталей, то такая модель называется вербальной.
Если построена физическая копия объекта, то такая модель называется натурной.
Если заданы графики взаимосвязей параметров объекта, то такая модель называется графической.

Моделирование объекта
Если объект описан формальными математиче-скими соотношениями (описаны взаимосвязи параметров), то это математическая модель объекта.
Математическая модель может иметь конкретное названия в зависимости от применяемого аппарата. Например, модель в виде дифферен-циального уравнения, стохастическая модель.
В этом курсе мы будем рассматривать только математические модели.
Для математического моделирования объекта выбираются существенные параметры объекта.

Моделирование объекта
Параметры объекта – это числа или переменные величины, принимающие числовые значения. Параметры могут быть управляемыми или неуправляемыми. Управляемые параметры – это переменные величины, числовые значения или зависимости для которых может выбирать исследователь. Неуправляемые параметры – это числа или переменные величины, значения которых исследователь не может изменять.
При построении аналитической модели строятся математические соотношения между параметрами.

Моделирование объекта
Переменные, входящие в модель (это управляе-мые и неуправляемые параметры объекта), могут быть детерминированными (это обычные переменные из высшей математики) и стохасти-ческими (или случайными) – это переменные величины из теории вероятностей и математи-ческой статистики. В соответствие с этим модель называется детерминированной или стохасти-ческой (случайной).
В радиоэлектронике и радиотехнике большинство моделей стохастические.

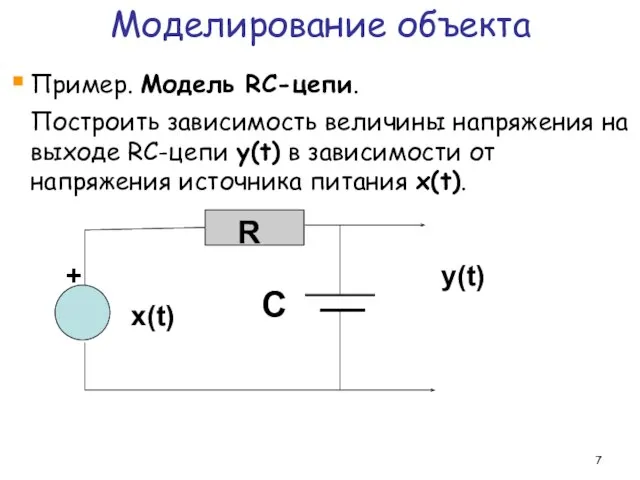
Моделирование объекта
Пример. Модель RC-цепи.
Построить зависимость величины напряжения на выходе RC-цепи y(t) в зависимости от напряжения источника питания x(t).
R
x(t)
+
C
y(t)

Моделирование объекта
Пример. Модель RC-цепи.
Для решения задачи необходимы знания предметной области. Если исследователь не имеет таких знаний, то требуется привлечение соответствующего специалиста. В данной задаче необходимо знание закона Ома и формулу заряда конденсатора.
Решение. Параметрами модели будут входящие в схему величины R и C. Пусть в момент времени t по сопротивлению R проходит ток i(t), а количество электричества на конденсаторе C равно Q(t). Тогда напряжение на сопротивлении равно R * i(t) (закон Ома), а на конденсаторе y(t) = Q(t)/C .

Моделирование объекта
Пример. Модель RC-цепи. Решение.
Тогда напряжение на генераторе равно напряжению в цепи
x(t) = R * i(t) + y(t). (1)
Кроме того,
i(t) = dQ(t)/dt = d(y(t)*C)/dt = C * y’(t).
Отсюда и из (1) получаем окончательное соотношение в виде дифференциального уравнения:
x(t) = С*R * y’(t) + y(t).

Моделирование объекта
y(t) + C R y’(t) = x(t)
-это линейное дифференциальное уравнение первого порядка. Общий вид такого уравнения
y(t) + p(t) y’(t) = f(t) (2).
Его решение :
где y1(t) – некоторое частное решение уравнения (2).
Для нашего уравнения p(t)=C R, интегрируя показатель степени, получаем:
Константу c1 получаем из начальных условий системы.

1.2. Моделирование системы
В реальной жизни исследуемый объект состоит из множества связанных между собой более простых объектов, процессов, явлений, объеди-ненных единой целью. Такой сложный объект будем называть системой, а его части назовем компонентами. При первом рассмотрении можно рассматривать систему как простой объект, не принимая во внимание наличие компонент.
Пример. Производственной предприятие терпит убытки, требуется провести его реструктуризацию.

Моделирование системы
При начальном рассмотрении можно принять во внима-ние только материалы, комплектующие, энергетические затраты производства, подсчитать их долю в себестои-мости единицы продукции и сравнить эти доли с анало-гичными затратами конкурентов. Если этот анализ не дает результата, то хорошим продолжением считается рассмотрение предприятия как системы, состоящей из взаимосвязанных компонент. Разумно в качестве компонент рассматривать отделы предприятия: администрацию, отдел кадров, бухгалтерию, плановый отдел, отдел снабжения, отдел маркетинга, цеха предприятия и т.п.
Далее следует изучить деятельность каждого отдела в отдельности, а затем работу отделов во взаимосвязи.

Моделирование системы
Примечание. Рассмотренная задача анализа производства в современном менеджменте называется задачей консалтинга.
При анализе системы обычно не строится общая модель системы – это трудно, а еще труднее анализировать такую модель. Строятся отдельные модели ее компонент и учитываются существенные взаимосвязи между компо-нентами. Такой подход в моделировании называется декомпозицией.
Построение общей модели системы без декомпозиции практически невозможно: компоненты системы разно-родны и их трудно описать в рамках одной математической теории.
Пример. Технологический процесс производства азота описывается уравнениями химических реакций, а работа отдела снабжения графами связей с поставщиками.

Моделирование системы
Пример системы. Стропы и ткань. Соединенные специальным образом, они образуют новый объект – парашют со свойствами, которыми не обладают исходные предметы. Можно изучить свойства строп и ткани по отдельности (прочность, воздухопроницаемость, …), но существенным будет схема соединения этих компонент и способ укладки парашюта.

Моделирование системы
Следует заметить, что во многих изобретениях исполь-зуется идея синтеза системы из менее сложных компо-нент. Примеры:
1) телефона + радиосвязью —> мобильная телефония;
2) электрический двигатель + автомобиль —> электро-мобиль;
3) установка боевой ракеты в ж/д вагоне —> мобильная пусковая установка;
4) USB слоты на экране компьютера —> удобство работы с флеш-памятью;
5) использование графического процессора для вычислений —> технология CUDA.

Моделирование системы
Решение задачи начинается с ее постановки, то есть :
1) определения объекта исследования,
2) формулировки цели исследования,
3) построения математической модели.
Говорят, что хорошая постановка задачи уже на 50% решает задачу.
Часто компоненты системы имеют несовпадающие или даже противоположные цели. В этом случае исследователь должен согласовать их. В процессе исследования цели могут уточняться, при этом некоторые параметра могут оказаться несущественными, а другие введены в модель как существенные. То есть, решение задачи – это процесс.
В нашем изложении основной частью постановки задачи является 3) моделирование.

Моделирование системы
Модель отражает цель исследования

Моделирование системы
Системный подход - комплексное изучение объекта как единого целого путем уточнение задачи и её декомпозицию в серию задач, решаемых с помощью методов естественных наук.
При декомпозиции в серию задач:
1) строятся локальные модели этих задач,
2) строится глобальная модель объединяющая локальные модели,
3) выбираются или создаются методы решения локальных задач,
4) выбирается или создается метод решения глобальной задачи.

Моделирование системы
Пример. Решение задачи обмена информацией в компьютерной сети методом декомпозиция.
Модель сетевого обмена OSI (Open Systems Interconnection).
OSI – теоретическая формальная модель (1984г) организации обмена в сети, детально описывающая сетевые обмены сообщениями.
Для упрощения задачи обмена была проведена ее декомпо-зиция, задачу разделили на 7 компонент (в данном конкретном случае уровней, слоев). Для каждого уровня создали локаль-ные модели в виде протоколов. Каждый уровень взаимодей-ствует не более, чем с двумя соседями, расположенных выше и ниже, это упрощает глобальную модель.
Набор связанных таким образом протоколов, которые обеспе-чивают обмен данными в сети, называется стеком протоколов.
Эта модель формализует задачу обмена в сети, указывая, какие задачи и в какой последовательности нужно решать.

Уровни OSI.
Моделирование системы

Моделирование системы
Системотехника - прикладная наука, исследующая задачи
1) анализа сложных управляющих систем;
2) Создания (синтеза) сложных управляющих систем.
Цель задачи анализа состоит в исследовании свойств системы. Для этого строится математическая или иная модель системы. Обычно система разделяется на компоненты и строятся модели для каждой компоненты. После этого строится глобальная модель, объединяющая модели компонент. Затем модели исследуются математи-ческими методами и полученные свойства математических решений интерпретируются на анализируемой реальной системе. Если полученные свойства соответствуют реаль-ной картине, то считаем, что анализ системы проведен успешно, иначе модели корректируются и уточняются.
В этом курсе изучаются только некоторые методы ана-лиза сигналов на основе интегральных преобразований.

Моделирование системы
Задача синтеза сложных управляющих систем. Процесс построения радиоэлектронной системы состоит из шести этапов:
1) Определение целей, составление планов работ.
2) Декомпозиция системы на компоненты, моделирование и проектирование компонент и всей системы.
3) Создание программного обеспечения.
4) Тестирование системы и ее ввод в действие.
5) Обслуживание и поддержка системы.
Это комплексная задача, ее решает команда из представителей разных специальностей. При участии в современных разработках важно уметь работать в команде.