Содержание
- 3. Определения Модуль числа а – расстояние от точки с координатой а до ноля следствия 1. модуль
- 4. Способы решения уравнений с модулями: 1. По определению модуля 2. Раскрытие модуля на промежутке знакопостоянства 6.
- 5. 1. По определению модуля |ƒ(x)| = a (а≥0) Пример : |3x - 8| = 5 Решение:
- 6. 1) |2x - 3| = 5 решение Решить по определению модуля
- 7. Решение 2x - 3 = 5 или 2x - 3 = -5 2x = 8 2x
- 8. 4.Раскрытие модуля на промежутке знакопостоянства Универсальный способ Решение: Найдем нули подмодульных выражений: 0; -1 -1 0
- 9. 1) |5 - x| + |x - 1| = 10 решение 3) |x - 1| +
- 10. + 1 + 5 - x - 1 5 - x - + + |5 -
- 11. - -1 - 3 + x + 1 x - 3 - + + |x -
- 12. - 1 - 1,5 + x - 1 2x - 3 - + + |x -
- 13. 6. Важный частный случай | f (x) | = - f(x), тогда f(x) ≤ 0 Пример:
- 15. Скачать презентацию
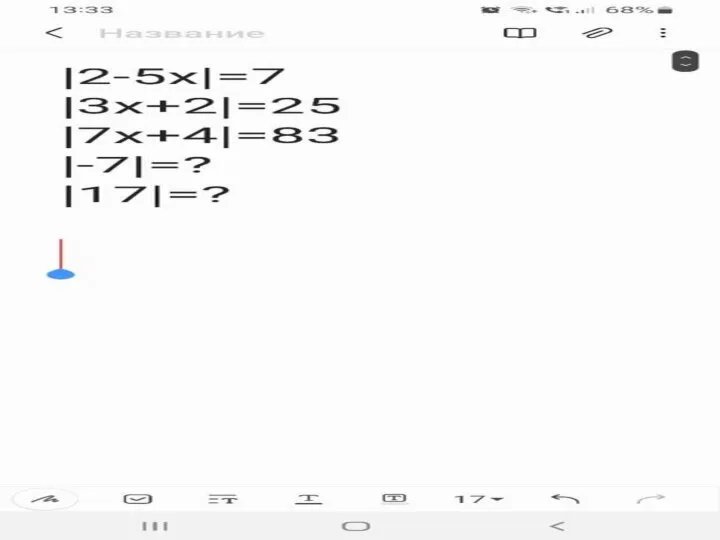











 Презентация на тему Роль и значение таможни в современной торговле
Презентация на тему Роль и значение таможни в современной торговле  Человек и источник света
Человек и источник света Современные популярные оздоровительные системы физических упражнений
Современные популярные оздоровительные системы физических упражнений Презентация на тему Межличностные отношения
Презентация на тему Межличностные отношения Интерактивные рисунки – визуальное средство обучения и контроля
Интерактивные рисунки – визуальное средство обучения и контроля Untitled - Made with DesignCap (7)
Untitled - Made with DesignCap (7) Мероприятия и Промоушены
Мероприятия и Промоушены Структура и содержание современного образования Англии
Структура и содержание современного образования Англии Projekt
Projekt Течение
Течение Leadership styles
Leadership styles Истоки развития научной концепции стресса. Стадии развития стресса
Истоки развития научной концепции стресса. Стадии развития стресса Основные направления социальной и образовательной интеграции
Основные направления социальной и образовательной интеграции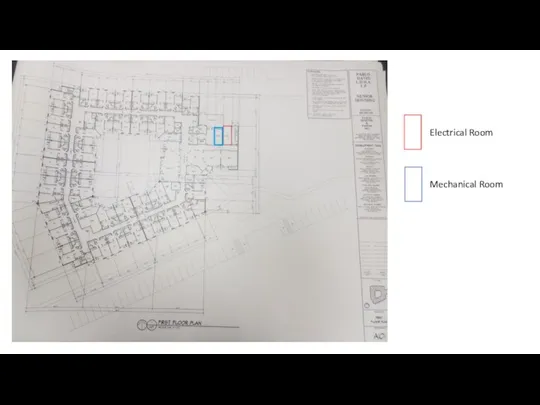 Pablo Equipment Location
Pablo Equipment Location Моя студенческая жизнь!
Моя студенческая жизнь! ЗАИМСТВОВАННЫЕ СЛОВА В РУССКОМ ЯЗЫКЕ
ЗАИМСТВОВАННЫЕ СЛОВА В РУССКОМ ЯЗЫКЕ Physio Radiance - Активируйте ваши клетки кожи
Physio Radiance - Активируйте ваши клетки кожи ВЕРИФИКАЦИЯ ПРОГРАММЫ COSMOS/M ДЛЯ РАСЧЕТА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ЭЛЕМЕНТОВ И УЗЛОВ ОБОРУДОВАНИЯ И ТРУБОПРОВОДОВ АЭУ
ВЕРИФИКАЦИЯ ПРОГРАММЫ COSMOS/M ДЛЯ РАСЧЕТА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ЭЛЕМЕНТОВ И УЗЛОВ ОБОРУДОВАНИЯ И ТРУБОПРОВОДОВ АЭУ Научный комплекс России
Научный комплекс России Антикоррупционная политика образовательной организации
Антикоррупционная политика образовательной организации Всероссийская олимпиада школьников 2022-2023
Всероссийская олимпиада школьников 2022-2023 Питание невидимок
Питание невидимок Эвтаназия. Статья 105. Убийство УК РФ
Эвтаназия. Статья 105. Убийство УК РФ Приёмы педагогической техники на уроке иностранного языка
Приёмы педагогической техники на уроке иностранного языка 12.09-16.09
12.09-16.09 МОУ «Деревянкская СОШ №5» Прионежский р-нпоселок Деревянка
МОУ «Деревянкская СОШ №5» Прионежский р-нпоселок Деревянка Презентация на тему Формы работы социального педагога
Презентация на тему Формы работы социального педагога ООО «Охранное предприятие «Масса-Юг»
ООО «Охранное предприятие «Масса-Юг»