Содержание
- 2. Молекулярная механика Основы: Симуляции подчиняются законам классической физики. Движущая сила : Функции потенциальной энергии, минимизация энергии,
- 3. Уравнение Ньютона Fi Ковалентные взаимодействия Не ковалентные взаимодействия
- 4. Силовое поле, константы Константы из уравнения : 1) связи , Кb, b0 ИР-спектроскопия, QM 2) углы
- 5. Молекулярная динамика Сумма сил действующих на атом Расчет новых координат Δt интегрирование
- 6. Методология подготовки системы для МД Построение топологии молекулы на основе координат т.е. перечисление связей углов и
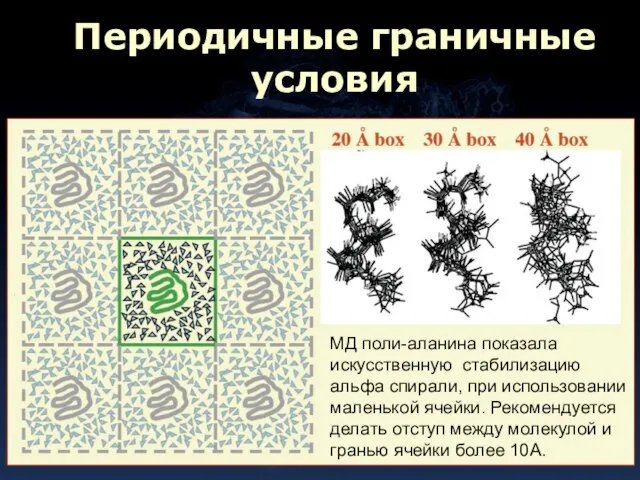
- 7. Периодичные граничные условия МД поли-аланина показала искусственную стабилизацию альфа спирали, при использовании маленькой ячейки. Рекомендуется делать
- 8. Что можно узнать из МД? равновесные свойства: Константа связывания лиганда с белком Средняя потенциальная энергия системы
- 9. Ограничения МД Симуляции основаны на законе Ньютона Электроны не учитываются Силовые поля это приближение Удалённые взаимодействия
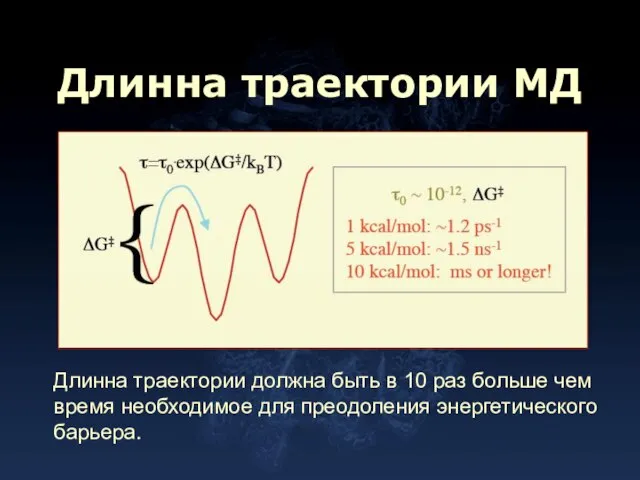
- 10. Длинна траектории МД Длинна траектории должна быть в 10 раз больше чем время необходимое для преодоления
- 11. Удаленные электростатические взаимодействия
- 12. Удаленные электростатические взаимодействия N2 Приемлемый выход это PME, particle mesh Ewald алгоритм. Использует FFT, быстрые преобразования
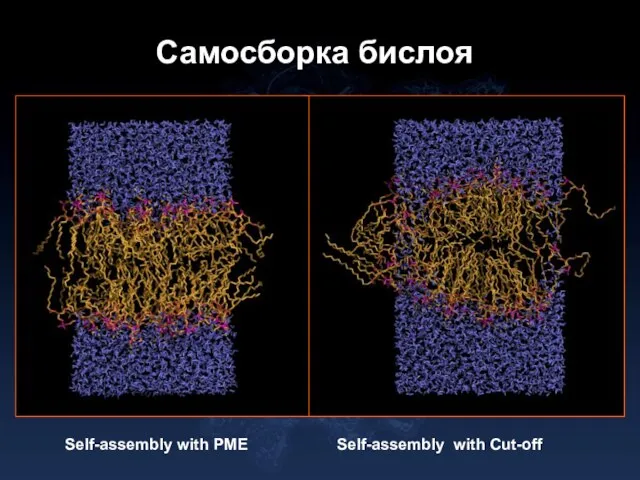
- 13. Самосборка бислоя Self-assembly with PME Self-assembly with Cut-off
- 14. Алгоритмы минимизации энергии системы hn максимальное смещение Steepest descent (крутой спуск) Если то новые координаты принимаются
- 15. Алгоритмы минимизации энергии системы Conjugate Gradient (сопряженный градиент) Окончание минимизации определяется значением максимальной силы в системе,
- 16. Алгоритмы минимизации энергии системы Очень эффективный алгоритм. Рекомендуется использовать вместе с PME. L-bfgs Строит обратный Гессиан
- 17. Увеличение шага интегратора МД Можно присвоить атому водорода массу 2 а.е. При этом отняв 1 от
- 18. Конструкции атомов-пустышек в GROMACS Атомы входящие в конструкцию Атомы - пустышки Время расчёта Используя атомы пустышки
- 19. МД с поляризацией (Shell MD) Используется поляризационная модель Дика и Оверхаузера. В этой модели частица представляющая
- 20. Стохастическая динамика Константа фрикции «Процесс шума» Используется при симуляции кристаллов
- 21. Броуновская динамика Коофицент фрикции «Процесс шума» Используется для изучения диффузии молекул. Можно использовать большой шаг. Алгоритм
- 22. Анализ нормальных мод Выявление гармонических колебаний молекулы. Последовательность использования программ пакета GROMACS: Mdrun –минимизация энергии. g_nmeig
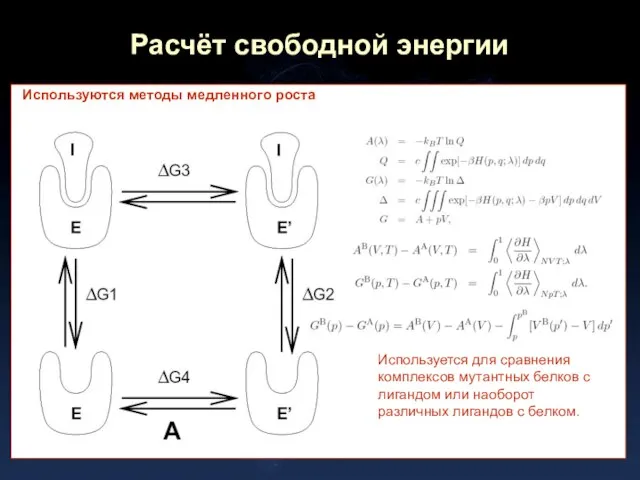
- 23. Расчёт свободной энергии Используются методы медленного роста Используется для сравнения комплексов мутантных белков с лигандом или
- 24. Существенная динамика (principal component analysis,essential dynamics)
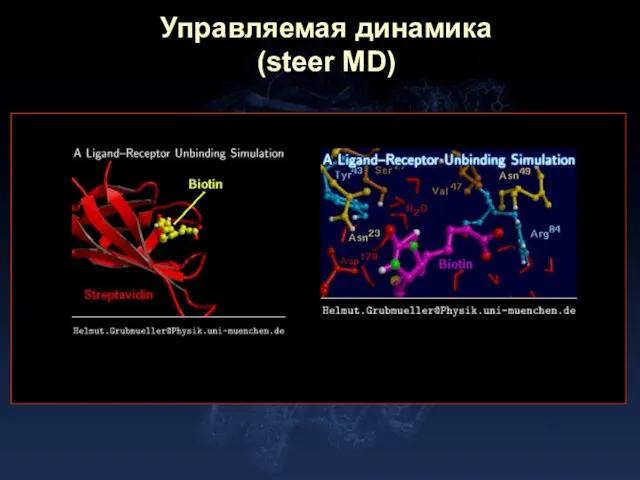
- 25. Управляемая динамика (steer MD)
- 26. Анализ траекторий Gromacs предоставляет более 50 программ для анализа траекторий. Можно выделить ряд групп: Общие свойства:
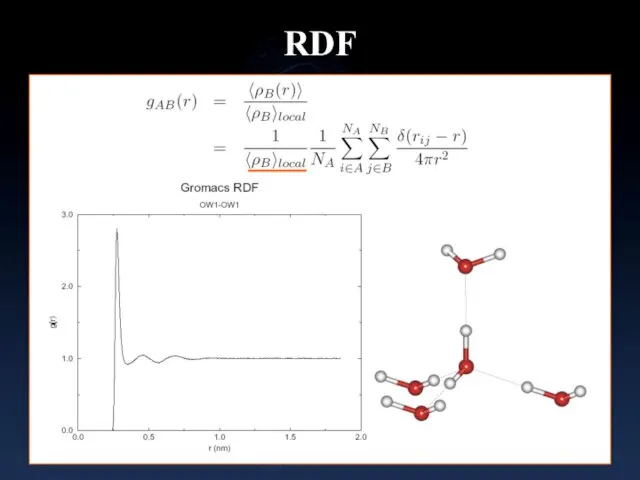
- 27. RDF
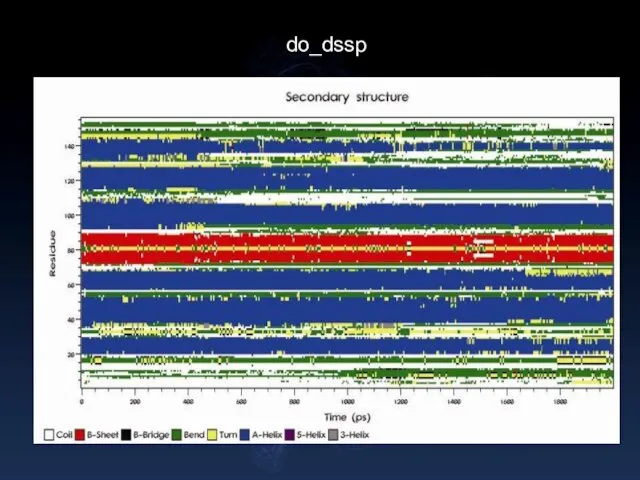
- 28. do_dssp
- 30. Скачать презентацию




















 Н. М. Карамзин и Симбирск
Н. М. Карамзин и Симбирск Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155
Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155 [Название]
[Название] Презентация на тему Образование в Японии
Презентация на тему Образование в Японии Междисциплинарная интеграция с использованием информационных технологий.
Междисциплинарная интеграция с использованием информационных технологий. МИФ или РЕАЛЬНОСТЬ?
МИФ или РЕАЛЬНОСТЬ? Исследователь и творец: какой он? ( 3 Межрегиональная конференция «Организация исследовательской деятельности детей и молодёжи: п
Исследователь и творец: какой он? ( 3 Межрегиональная конференция «Организация исследовательской деятельности детей и молодёжи: п Турция
Турция Нас ждет глобальное потепление! Льды растают и затопят низменные участки земли
Нас ждет глобальное потепление! Льды растают и затопят низменные участки земли Сказки М.Е. Салтыкова-Щедрина.
Сказки М.Е. Салтыкова-Щедрина. Умножение на 4
Умножение на 4 Загадка смерти Александра I
Загадка смерти Александра I Тушь Extreme Fashion
Тушь Extreme Fashion МАСТЕР-КЛАСС Критериально-ориентированное педагогическое тестирование Модуль № 2. Внутренняя экспертизатестов
МАСТЕР-КЛАСС Критериально-ориентированное педагогическое тестирование Модуль № 2. Внутренняя экспертизатестов Australian financial services consulting company (fintech)
Australian financial services consulting company (fintech) Афиши к спектаклю по драме А. Островского Гроза
Афиши к спектаклю по драме А. Островского Гроза Мастер - класс по нетрадиционным техникам рисования
Мастер - класс по нетрадиционным техникам рисования 1 сентября – День знаний
1 сентября – День знаний Физика и искусство
Физика и искусство Автомобильная промышленность
Автомобильная промышленность Арт менеджмент
Арт менеджмент  Бакалаврская работа. Анализ проектного финансирования как средства стимулирования экономического роста региона
Бакалаврская работа. Анализ проектного финансирования как средства стимулирования экономического роста региона Диагностика электоральной ситуации перед выборами в Государственную Думу РФПо заказу РЦОИТ при ЦИК РФ
Диагностика электоральной ситуации перед выборами в Государственную Думу РФПо заказу РЦОИТ при ЦИК РФ РОЛЬ КАРТОГРАФИИ В РАЗВИТИИ ОБЩЕСТВА
РОЛЬ КАРТОГРАФИИ В РАЗВИТИИ ОБЩЕСТВА о картофеле
о картофеле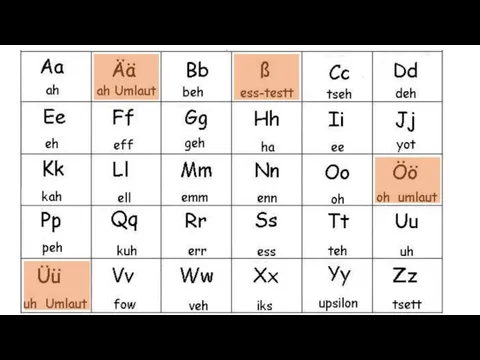 алфавит + звуки
алфавит + звуки Нарезание резьбы
Нарезание резьбы INFECTION CONTROL IN ICU
INFECTION CONTROL IN ICU