Молекулярная физика и основы термодинамики

Основные газовые законы
Закон Дальтона:
Закон Бойля-Мариотта: P⋅V=const при t0=const
Закон Шарля: P/T=const при V=const
Закон Гей-Люссака: V/T=const при P=const
Закон Авогадро: одинаковые количества газов при одинаковых температуре и давлении занимают одинаковый объём

Основные газовые законы
Законы Шарля и Гей-Люссака имеют такой простой вид если температура измеряется по абсолютной шкале
Первоначально эти законы были сформулированы для температуры, измеренной в некоторой практической шкале. В этом случае они имеют более сложный вид:
P=P0[1+α⋅(t-t0)]
V=V0[1+β⋅(t-t0)]
при чём коэффициенты α и β оказались равными и не зависящими от рода газа

Основные газовые законы
Процессы, описываемые уравнениями
2-4 называются изопроцессами:
Изотермическим
Изохорным
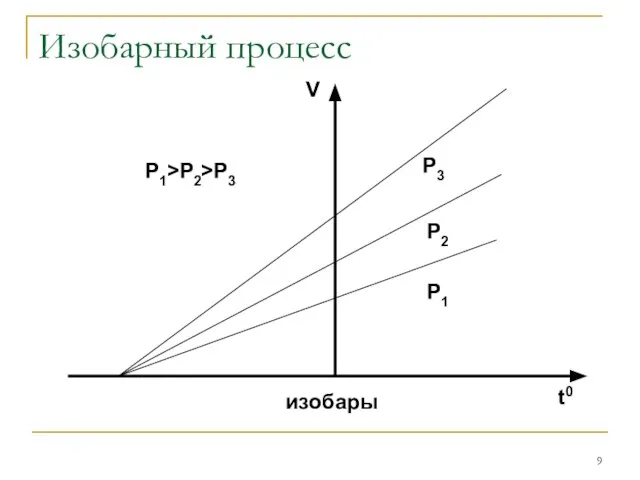
Изобарным

Изотермический процесс

Изотермический процесс

Изохорный процесс

Изохорный процесс

Изобарный процесс

Изобарный процесс

Основные газовые законы
Если измерять температуру по шкале Цельсия, то оказывается, что точка пересечения изохорного и изобарного процессов с осью температур имеет координату t=-373,15 0С. Это значит, что α=β=1/273,15 1/0С

Основные газовые законы
Если ввести новую шкалу температур, такую, что Т=t+273,15, то уравнения примут более простой вид:
P/T=const
V/T=const
Определённая таким образом температура называется абсолютной температурой

Основные газовые законы
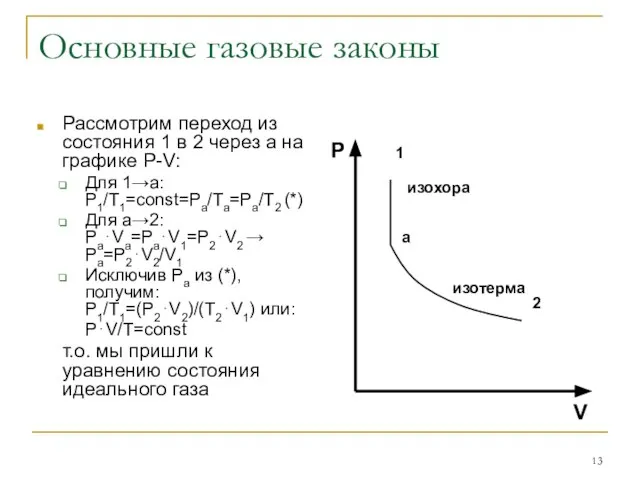
Рассмотрим переход из состояния 1 в 2 через а на графике P-V:
Для 1→а: P1/T1=const=Pa/Ta=Pa/T2 (*)
Для а→2: Pa⋅Va=Pa⋅V1=P2⋅V2 → Pa=P2⋅V2/V1
Исключив Ра из (*), получим: P1/T1=(P2⋅V2)/(T2⋅V1) или:
P⋅V/T=const
т.о. мы пришли к уравнению состояния идеального газа

Основные газовые законы
Из закона Авогадро следует, что величина соотношения (P⋅V)/T не зависит от вида газа, значит мы можем записать, что для одного моля любого газа (P⋅V)/T=R, где R – универсальная газовая постоянная, называемая постоянной Авогадро
R=8,31 Дж/(град⋅моль)
Из закона Дальтона следует, что при постоянных V и Т, Р является линейной функцией количества вещества ν

Основные газовые законы
Т.о., мы пришли к уравнению Клапейрона-Менделеева:
P⋅V=ν⋅R⋅T
или
P⋅V=(m/μ)⋅R⋅T

Основные газовые законы
Идеальный газ
Идеальным называется такой газ, который подчиняется закону Клапейрона-Менделеева
Поведение реальных газов приближается к поведению идеального газа в пределе низких давлений и высоких температур
Размеры молекул идеального газа малы по сравнению с межмолекулярным расстоянием, а энергией взаимодействия молекул можно пренебречь

Кинетическая теория газов
Оценка размеров молекул
Средний размер молекул
=(V/N)1/3, где V – объём, а N – количество молекул
Для воды: ρ=1г/см3, μ=18 г/моль → Vμ=18 см3.
=(Vμ/NA)1/3=(18/6⋅1023)1/3≈3⋅10-8 см=
=3⋅10-10 м

Кинетическая теория газов
Оценка расстояния между молекулами в газе
<>=(V/NA)1/3, при комнатной температуре и атмосферном давлении 1 моль газа занимает объём 22 400 см3 →
<>=(22400/6⋅1023)1/3≈3,3⋅10-7 см
Т.о. <> на порядок больше, чем
, соответственно, объём на три порядка больше

Кинетическая теория газов
Оценка средней длины свободного пробега молекул в газах
λ~<>⋅(<>/
)2
При нормальном давлении λ~10-5 см, то есть на два порядка больше <>

Кинетическая теория газов
Задача МКТ заключается в установлении взаимосвязи между макроскопическими параметрами ТД системы (P, T и др.) и её микроскопическими характеристиками (λ, μ,
,
, <>)

Вывод основного уравнения МКТ
Рассмотрим цилиндр с площадью основания S=1, опирающийся на стенку сосуда
Примем следующую модель
Частицы разделены на три равные группы, каждая из которых движется вдоль одной из координатных осей
Частицы не взаимодействуют между собой
При ударе частицы о стенку, на неё действует сила
i такая, что:
i⋅τ=Δpix≈2⋅ pix (*)

Вывод основного уравнения МКТ
Число ударов о стенку:
zi=S⋅ni⋅vix⋅Δt
Заменим в (*)
i на <
> так, что
i⋅τ=<
> ⋅Δt
Тогда, полная сила, действующая на стенку со стороны молекул, имеющих скорость vix:
Fix=zi⋅2⋅ pix/Δt=S⋅ni⋅vix⋅ pix

Вывод основного уравнения МКТ
→ P=ΣFi/S=Σni⋅vix⋅ pix=n⋅
=1/3⋅n⋅
⋅
=(2/3)⋅n⋅
Таким образом мы получили основное уравнение молекулярно-кинетической теории газов:
Р=(2/3)⋅n⋅

Оценка скорости молекул
Р=(2/3)⋅n⋅
=(2/3)⋅n⋅m⋅
/2=
=N⋅m⋅
/(3⋅V)=M⋅
/(3⋅V) →
→
=3⋅P⋅V/M=3⋅P/ρ →

Оценка скорости молекул
Для молекул водорода Н2 μ=2⋅10-3 кг/моль,
при комнатной температуре:
≈1800 м/с
для молекул О2 μ=2⋅10-3 кг/моль, при комнатной температуре:
≈500 м/с

Кинетическая теория газов
Сравнивая уравнение Клапейрона-Менделеева:
P=ν⋅R⋅T/V, где ν/V=n/Na
с основным уравнением молекулярно-кинетической теории газов:
Р=(2/3)⋅n⋅
мы можем заключить что:
R⋅T/NA=(2/3)⋅

Кинетическая теория газов
Окончательно получаем:
=(3/2)⋅k⋅T
где k – постоянная Больцмана
k=1,38⋅10-23 Дж/град
k=R/NA
Т.о. мы выяснили молекулярно-кинетический смысл температуры – она пропорциональна средней кинетической энергии молекулы

Кинетическая теория газов
Из Р=(2/3)⋅n⋅
и
=(3/2)⋅k⋅T
следует что:
P=n⋅k⋅T