Содержание
- 2. Пересечение поверхности плоскостью общего положения
- 3. Линия пересечения поверхности с плоскостью является линией, одновременно принадлежащей поверхности и секущей плоскостью. Поэтому необходимо построить
- 4. Линия пересечения строится с использованием метода секущих плоскостей – посредников или способом перемены плоскостей проекций. Способ
- 5. Пересечение многогранников плоскостью общего положения.
- 6. При сечении многогранника плоскостью образуется ломанная линия. Проекциями сечения многогранников, в общем случаи являются многоугольники, вершины
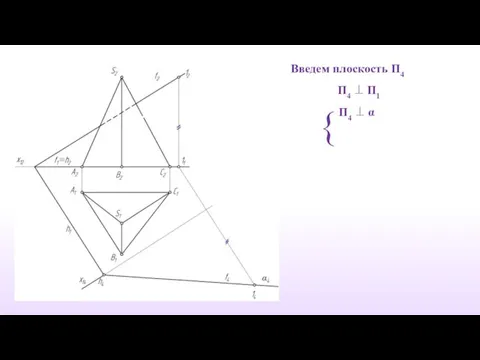
- 7. Задача 1 Пирамида Φ{SABC} и плоскость α(h,f) m=Ф∩α; m{M,N,K} - ? Ребро SB – профильная прямая.
- 8. Введем плоскость П4 П4 ⊥ П1 П4 ⊥ α {
- 9. Построим пирамиду Φ{SABC} на плоскости П4. Ребро SВ – прямая общего положения.
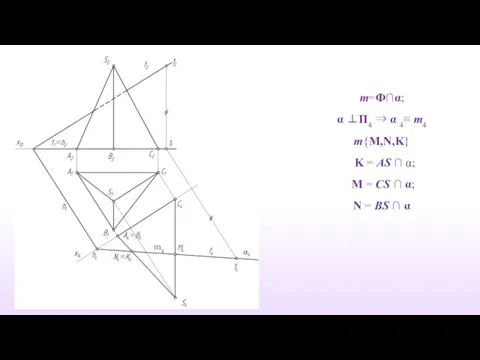
- 10. m=Ф∩α; α ⊥П4 ⇒ α 4≡ m4 m{M,N,K} K = AS ∩ α; M = CS
- 11. Проецируем точки пересечения K = AS ∩ α; M = CS ∩ α; N = BS
- 12. m1{M1,N1,K1} m1 m4
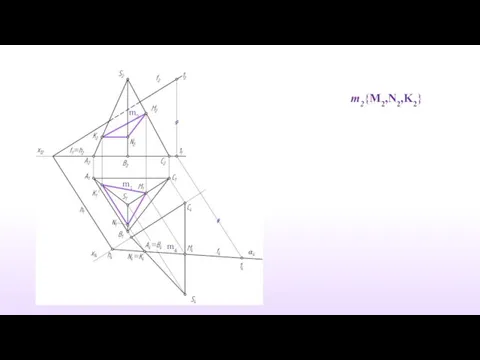
- 13. m2{M2,N2,K2} m4 m1 m2
- 14. Определить видимость сечения m2 m1 m4
- 15. Задача по определению сечения многогранника сводится к многократному решению задач: Определение точки пересечения прямой (ребер многогранника)
- 16. Линия пересечения строится с использованием метода секущих плоскостей – посредников Задача 2 Пирамида Φ{ТABC} и плоскость
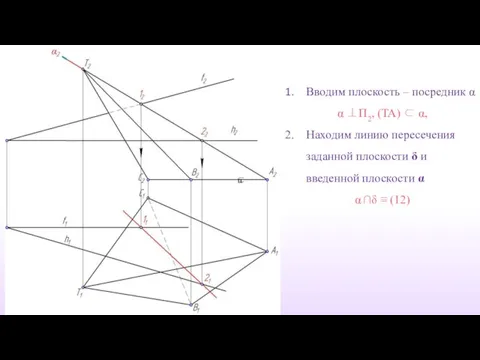
- 17. Вводим плоскость – посредник α α ⊥П2, (TA) ⊂ α, Находим линию пересечения заданной плоскости δ
- 18. Точка пересечения построенной прямой (12) с ребром (TA) есть первая точка линии пересечения (12) ∩ (TA)
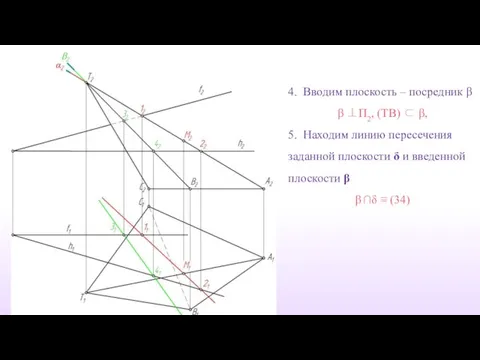
- 19. 4. Вводим плоскость – посредник β β ⊥П2, (TB) ⊂ β, 5. Находим линию пересечения заданной
- 20. 6. Точка пересечения построенной прямой (34) с ребром (TB) есть точка линии пересечения (34) ∩ (TB)
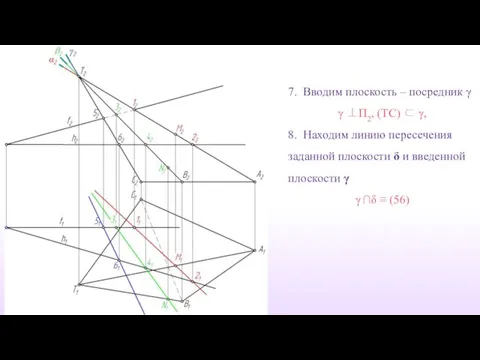
- 21. 7. Вводим плоскость – посредник γ γ ⊥П2, (TC) ⊂ γ, 8. Находим линию пересечения заданной
- 22. 9. Точка пересечения построенной прямой (56) с ребром (TС) есть точка линии пересечения (56) ∩ (TС)
- 23. 10. Строим линию пересечения m≡Ф∩δ; m{M,N,L}
- 24. Определяем видимость построенной линии пересечения m{M,N,L}
- 25. Пересечение поверхностей вращения плоскостью общего положения.
- 26. Алгоритм решения задач на пересечение поверхности с плоскостью общего положения Образующую поверхности заключаем во вспомогательную плоскость
- 27. Количество точек, используемых для построения линии пересечения, определяется формой поверхности и точностью построения. Но из всего
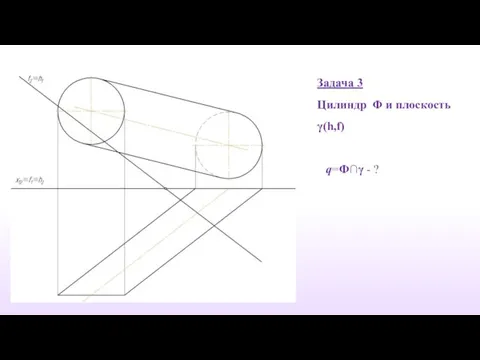
- 28. Задача 3 Цилиндр Φ и плоскость γ(h,f) q=Ф∩γ - ?
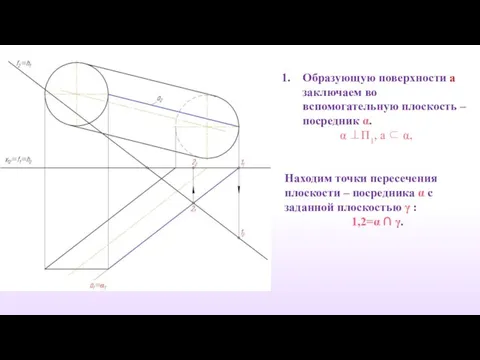
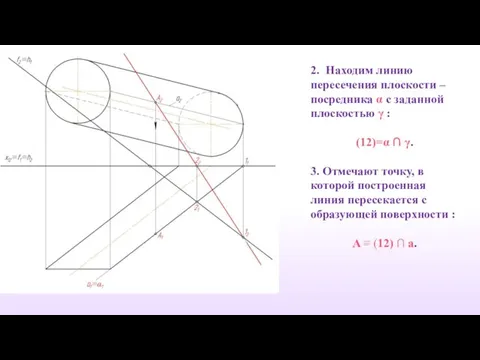
- 29. Образующую поверхности a заключаем во вспомогательную плоскость – посредник α. α ⊥П1, а ⊂ α, Находим
- 30. 2. Находим линию пересечения плоскости – посредника α с заданной плоскостью γ : (12)=α ∩ γ.
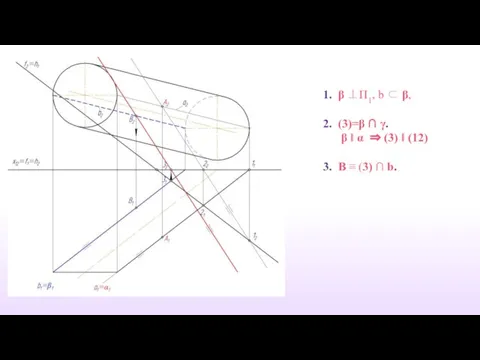
- 31. 1. β ⊥П1, b ⊂ β, 2. (3)=β ∩ γ. β ‖ α ⇒ (3) ‖
- 32. 1. φ ⊥П1, c ⊂ φ, 2. (4)= φ ∩ γ. φ ‖ α ⇒ (4)
- 33. 1. δ ⊥П1, d ⊂ δ, 2. (5)= δ ∩ γ. δ ‖ α ⇒ (5)
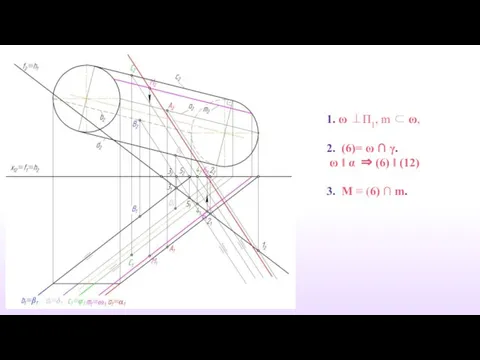
- 34. 1. ω ⊥П1, m ⊂ ω, 2. (6)= ω ∩ γ. ω ‖ α ⇒ (6)
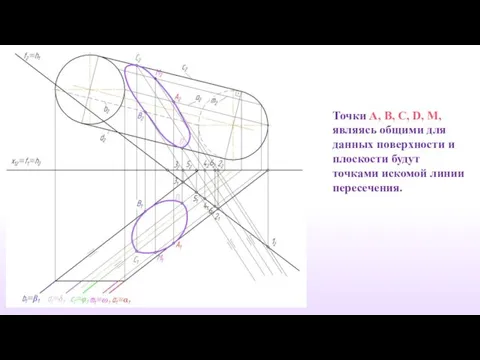
- 35. Точки A, B, C, D, М, являясь общими для данных поверхности и плоскости будут точками искомой
- 36. Определяем видимость сечения.
- 37. Плоскость пересекает сферу по окружности, проекции которой в общем случае на ортогональном чертеже изобразится эллипсами. Точки
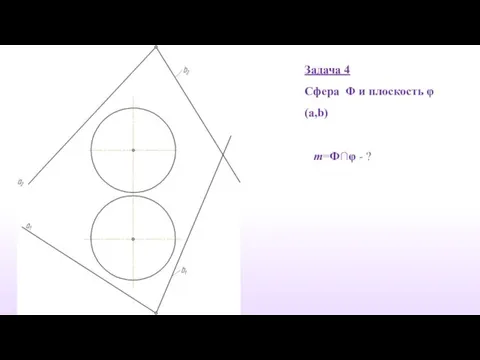
- 38. Задача 4 Сфера Φ и плоскость φ(a,b) m=Ф∩φ - ?
- 39. Вводим вспомогательную плоскость – посредник α через экватор. α ‖ П1 Находим точки пересечения плоскости –
- 40. Вводим вспомогательную плоскость – посредник β через главный меридиан. β ‖ П2 Находим точки пересечения плоскости
- 41. Для уточнения линии пересечения строим промежуточные точки. Вводим произвольно вспомогательную плоскость – посредник γ. γ ‖
- 42. Находим точки пересечения построенной окружности сечения сферы и горизонтали сечения плоскости φ: M,N = (56) ∩
- 43. n1 Вводим произвольно вспомогательную плоскость – посредник δ. δ ‖ П1 Находим точки пересечения плоскости –
- 44. Находим точки пересечения построенной окружности сечения сферы и горизонтали сечения плоскости φ: K,L = (78) ∩
- 45. Точки A, B, C, D, М, N, K, L, являясь общими для данных поверхности и плоскости
- 47. Скачать презентацию































 Отдельные виды договорных отношений в жилищном праве
Отдельные виды договорных отношений в жилищном праве Организация велостоянки для гимназии №1
Организация велостоянки для гимназии №1 О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го
О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го Урок русского языка в 6 классе по теме: «Правописание сложных существительных»
Урок русского языка в 6 классе по теме: «Правописание сложных существительных» Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании
Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании Невидимые нити в весеннем лесу (2 класс)
Невидимые нити в весеннем лесу (2 класс) Игрушки из носочков своими руками №7
Игрушки из носочков своими руками №7 Введение в специальность
Введение в специальность Герцог Ами
Герцог Ами Трение. Вредно или полезно
Трение. Вредно или полезно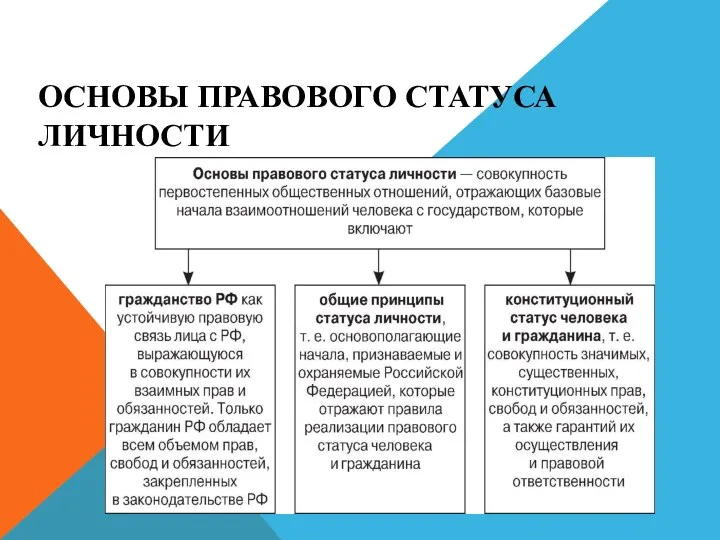 Правовой статус личности. Гражданство РФ
Правовой статус личности. Гражданство РФ Социальная психология
Социальная психология Презентация на тему АФАНАСИЙ НИКИТИН
Презентация на тему АФАНАСИЙ НИКИТИН  Теория обучения
Теория обучения Презентация на тему Our Environment (Наша окружающая среда)
Презентация на тему Our Environment (Наша окружающая среда) Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС)
Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС) Презентация по информатике на тему: «Устройства вывода информации, монитор.»
Презентация по информатике на тему: «Устройства вывода информации, монитор.» Круглопольское сельское поселение
Круглопольское сельское поселение Прайс косметологических услуг салона Забота о вас
Прайс косметологических услуг салона Забота о вас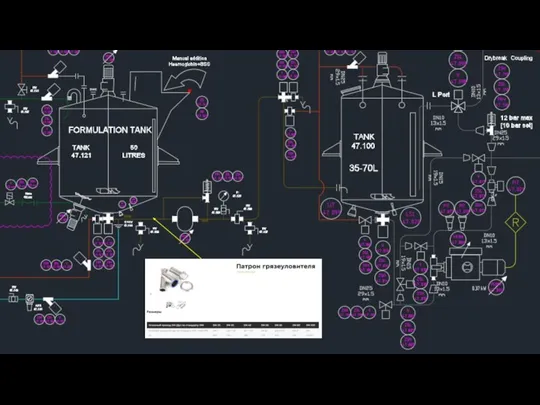 Патрон грязеуловителя
Патрон грязеуловителя Назначение изделия и его описание
Назначение изделия и его описание Планирование и организация процесса закупок материальных ресурсов промышленного предприятия
Планирование и организация процесса закупок материальных ресурсов промышленного предприятия Распространение объектно-ориентированного подхода на информационную безопасность
Распространение объектно-ориентированного подхода на информационную безопасность Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк.
Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк. Пейзаж в графике
Пейзаж в графике Рогожка. Коллекция однотонных штор
Рогожка. Коллекция однотонных штор _Презентация. Предоставление
_Презентация. Предоставление Презентация
Презентация