Содержание
- 2. ОСНОВОПОЛОЖНИКИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Альберти (Alberti) Леон Баттиста (18.2.1404 - 25.4.1472) Основатель теоретической перспективы. Гаспар Монж (1746-1818)
- 3. ОСНОВОПОЛОЖНИКИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Курдюмов Валериан Иванович (1853 - 1904) Издал полный курс начертательной геометрии, по обширной
- 4. ЛЕКЦИЯ 1 МЕТОДЫ ПРОЕЦИРОВАНИЯ Центральный метод проецирования П’ – плоскость проекций; S – центр проекций; [SA)
- 5. Параллельный метод проецирования П’ – плоскость проекций; s – направление проецирования; [SA), [SB) и [SC) –
- 6. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ Направление проецирования перпендикулярно плоскости проекций
- 7. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ П1- горизонтальная плоскость проекций; П2- фронтальная плоскость проекций; П3- профильная
- 8. ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ А1- горизонтальная проекция точки А; А2- фронтальная проекция точки А;
- 9. ТРЕХКАРТИННЫЙ КОМПЛЕКСНЫЙ ЧЕРТЕЖ ТОЧКИ (ЭПЮР МОНЖА) Чертеж на трех совмещенных плоскостях проекций называется трехкартинным комплексным чертежом
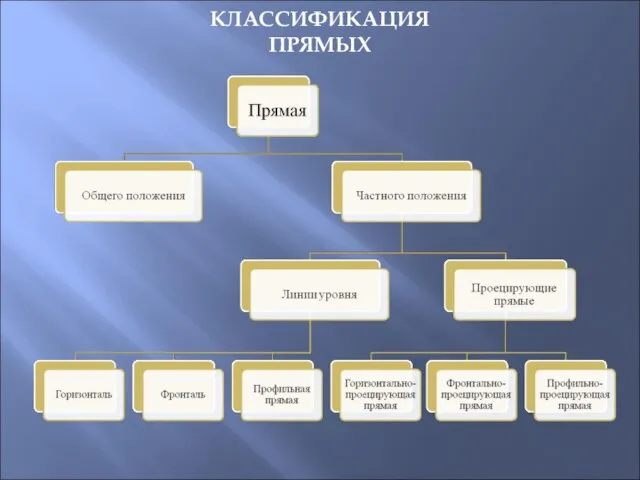
- 10. ЛЕКЦИЯ 2 ПРЯМАЯ ЛИНИЯ Способы задания прямой Двумя точками. Точкой и направлением. Линией пересечения двух плоскостей.
- 11. КЛАССИФИКАЦИЯ ПРЯМЫХ
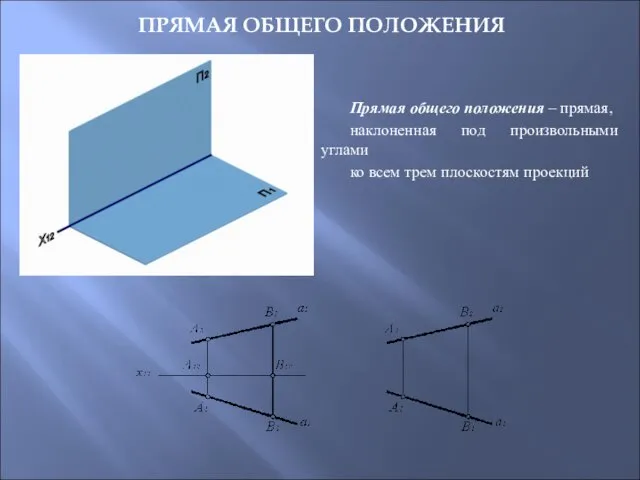
- 12. Прямая общего положения – прямая, наклоненная под произвольными углами ко всем трем плоскостям проекций ПРЯМАЯ ОБЩЕГО
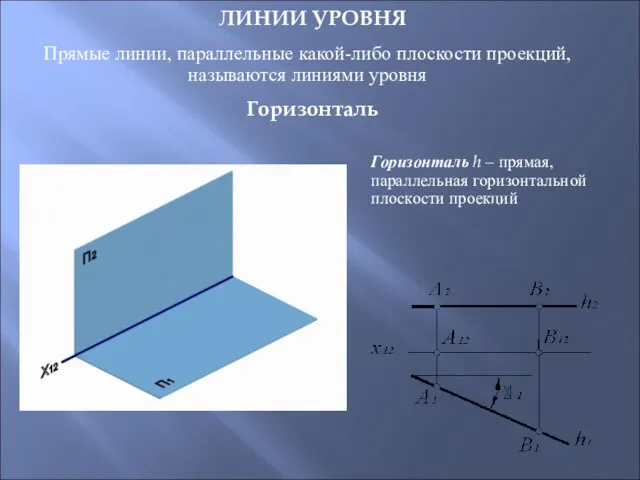
- 13. ЛИНИИ УРОВНЯ Прямые линии, параллельные какой-либо плоскости проекций, называются линиями уровня Горизонталь h – прямая, параллельная
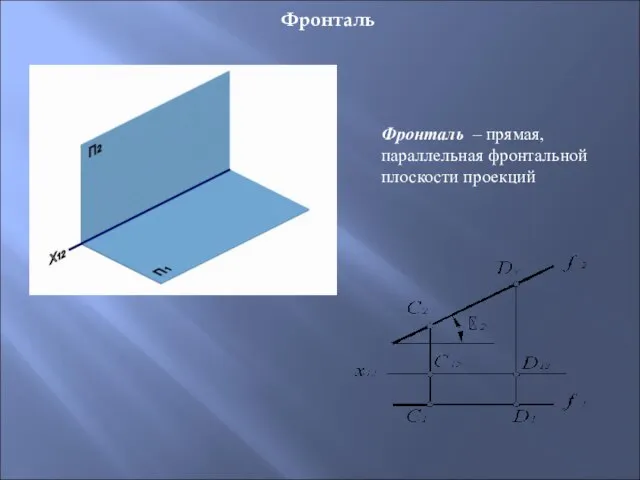
- 14. Фронталь Фронталь – прямая, параллельная фронтальной плоскости проекций
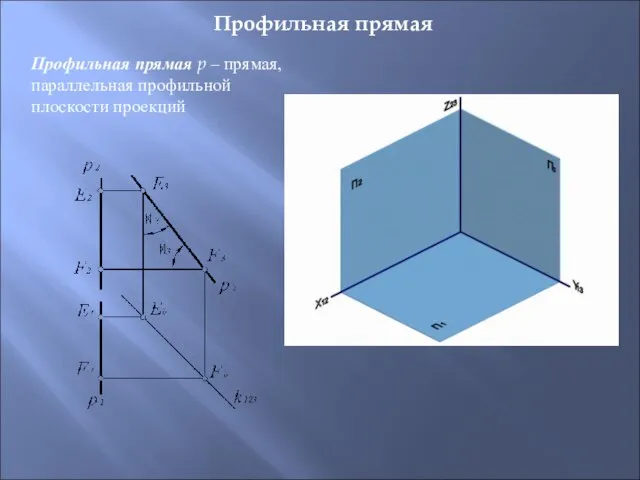
- 15. Профильная прямая Профильная прямая p – прямая, параллельная профильной плоскости проекций
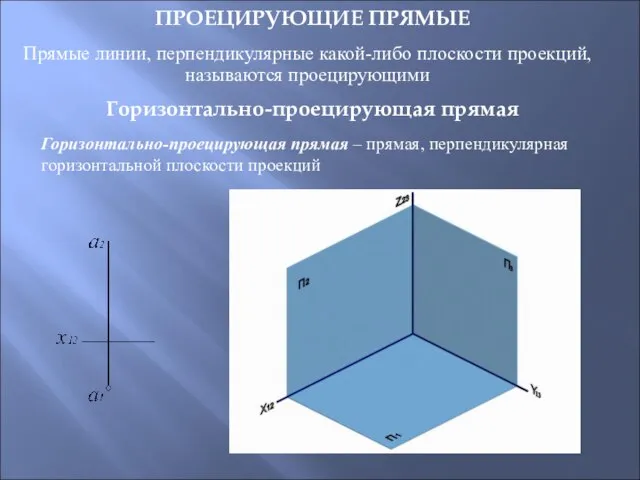
- 16. ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ Прямые линии, перпендикулярные какой-либо плоскости проекций, называются проецирующими Горизонтально-проецирующая прямая – прямая, перпендикулярная горизонтальной
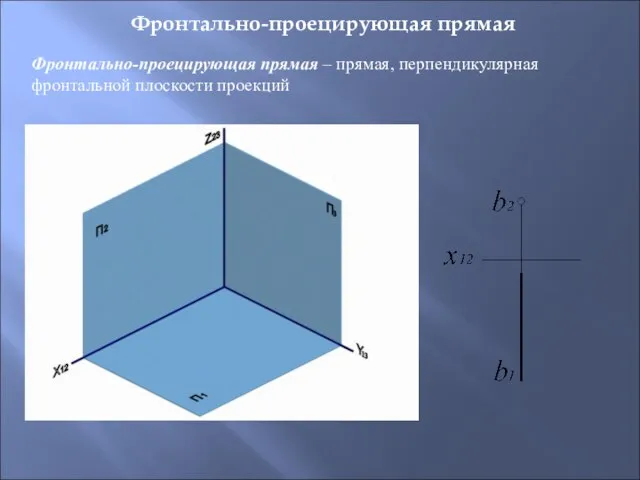
- 17. Фронтально-проецирующая прямая Фронтально-проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций
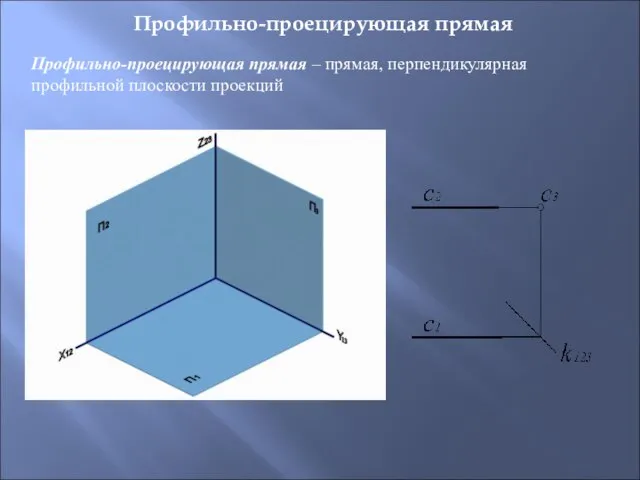
- 18. Профильно-проецирующая прямая Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций
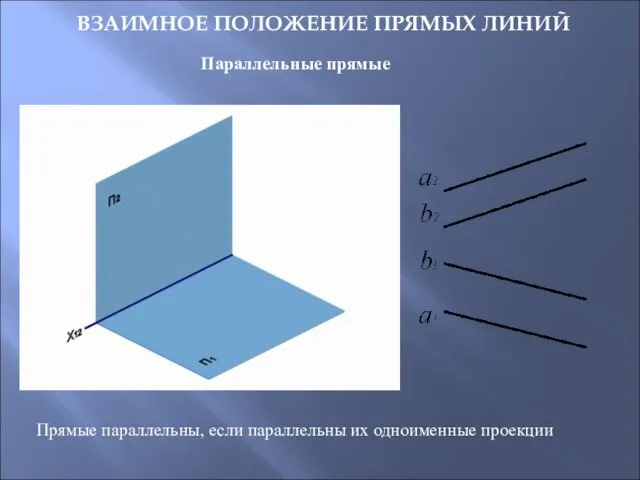
- 19. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ ЛИНИЙ Параллельные прямые Прямые параллельны, если параллельны их одноименные проекции
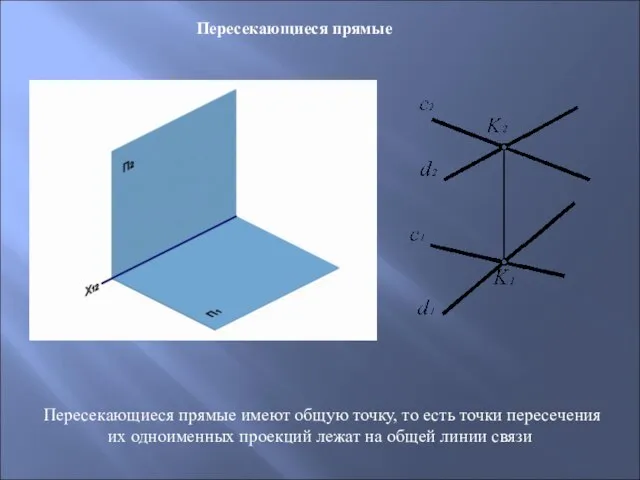
- 20. Пересекающиеся прямые Пересекающиеся прямые имеют общую точку, то есть точки пересечения их одноименных проекций лежат на
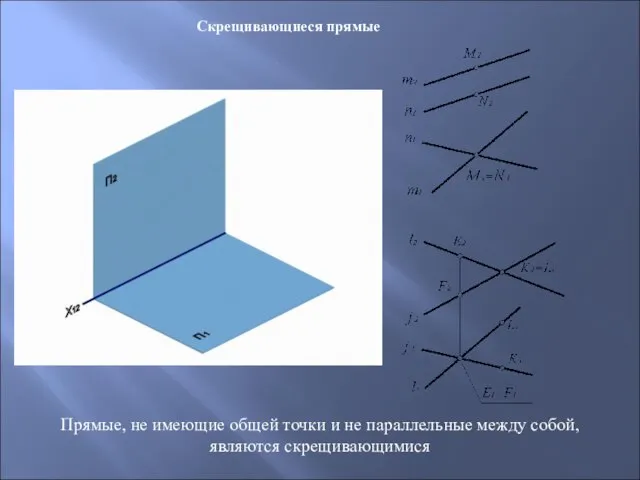
- 21. Скрещивающиеся прямые Прямые, не имеющие общей точки и не параллельные между собой, являются скрещивающимися
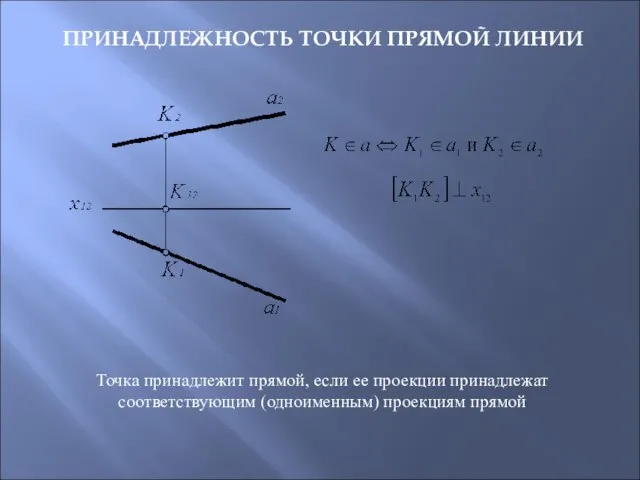
- 22. ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПРЯМОЙ ЛИНИИ Точка принадлежит прямой, если ее проекции принадлежат соответствующим (одноименным) проекциям прямой
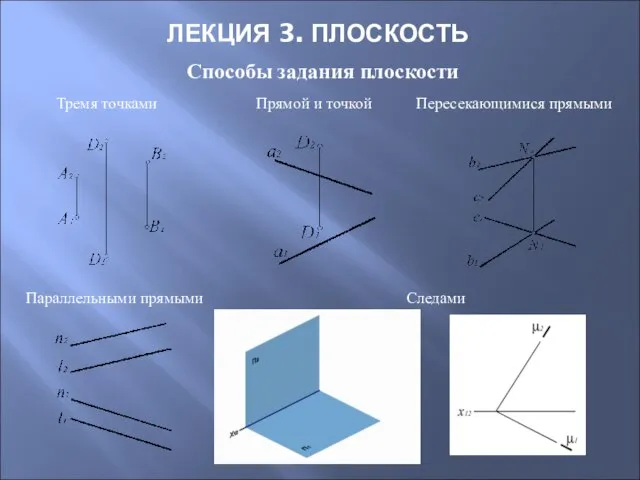
- 23. ЛЕКЦИЯ 3. ПЛОСКОСТЬ Способы задания плоскости Тремя точками Пересекающимися прямыми Прямой и точкой Параллельными прямыми Следами
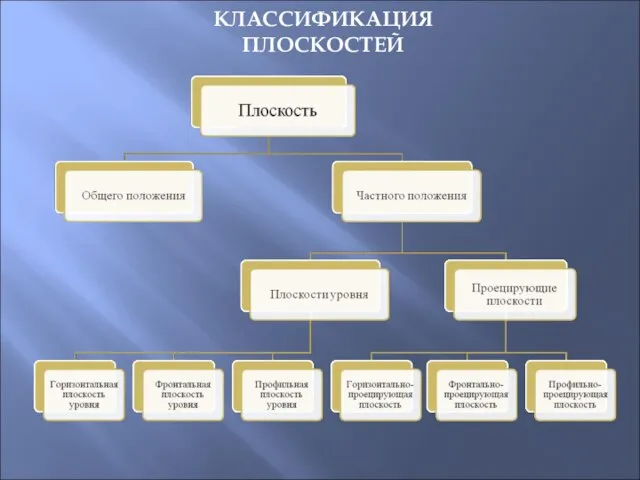
- 24. КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ
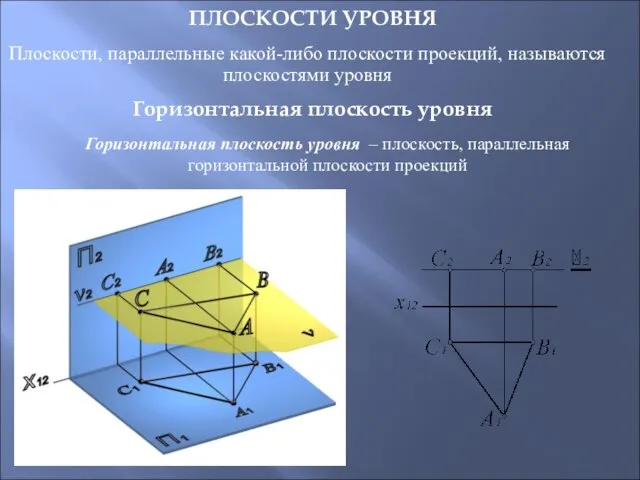
- 25. ПЛОСКОСТИ УРОВНЯ Плоскости, параллельные какой-либо плоскости проекций, называются плоскостями уровня Горизонтальная плоскость уровня – плоскость, параллельная
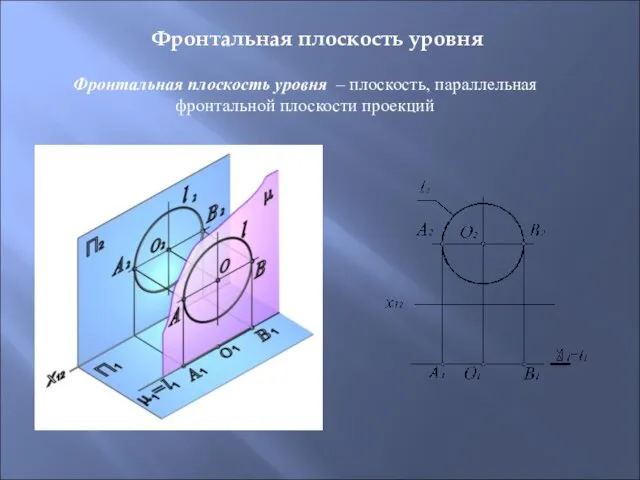
- 26. Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций Фронтальная плоскость уровня
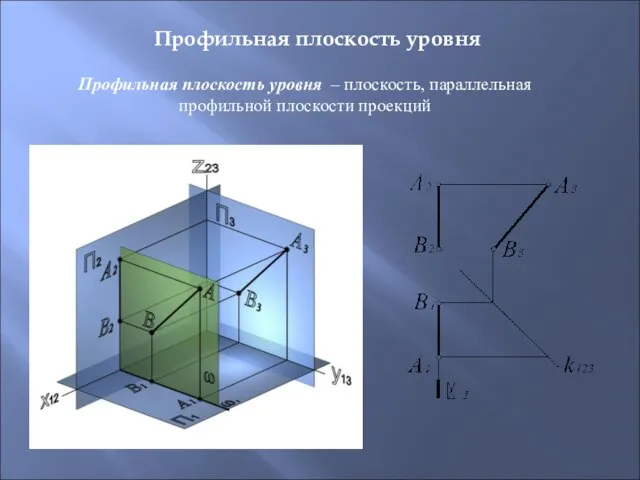
- 27. Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций Профильная плоскость уровня
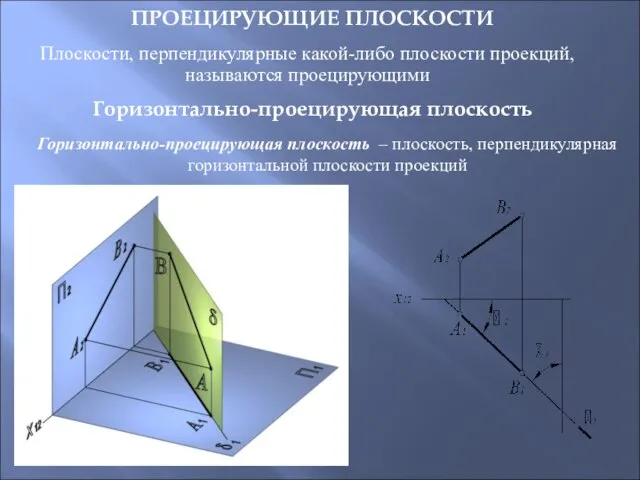
- 28. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ Плоскости, перпендикулярные какой-либо плоскости проекций, называются проецирующими Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости
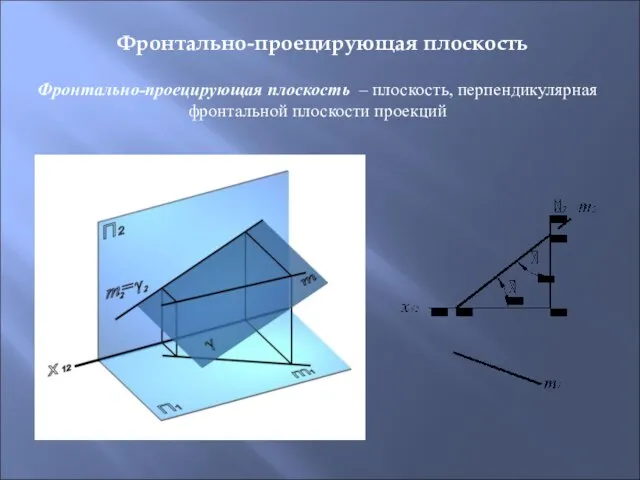
- 29. Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций Фронтально-проецирующая плоскость
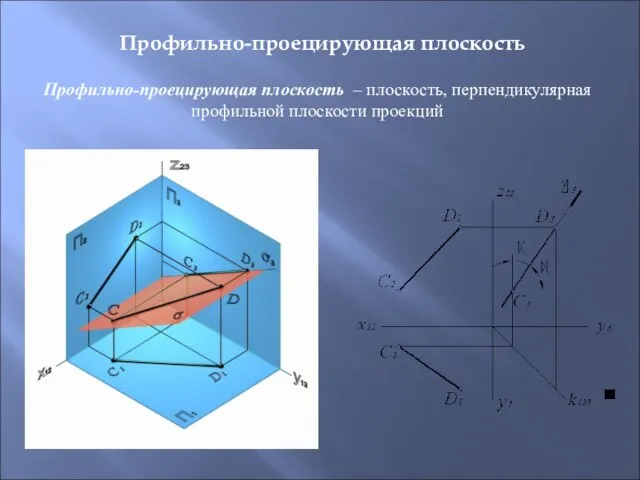
- 30. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций Профильно-проецирующая плоскость
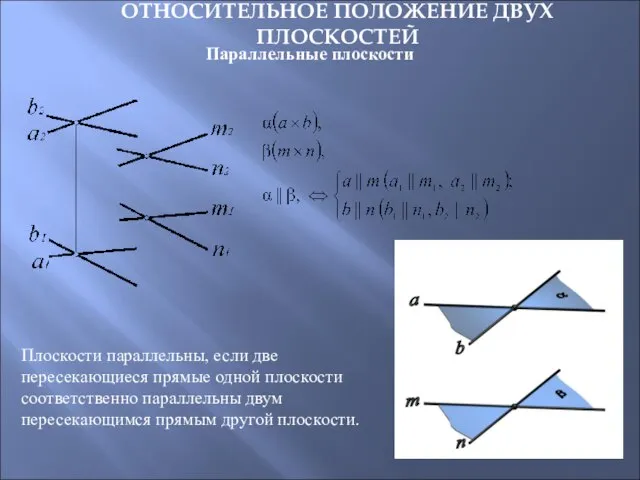
- 31. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ Параллельные плоскости Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны
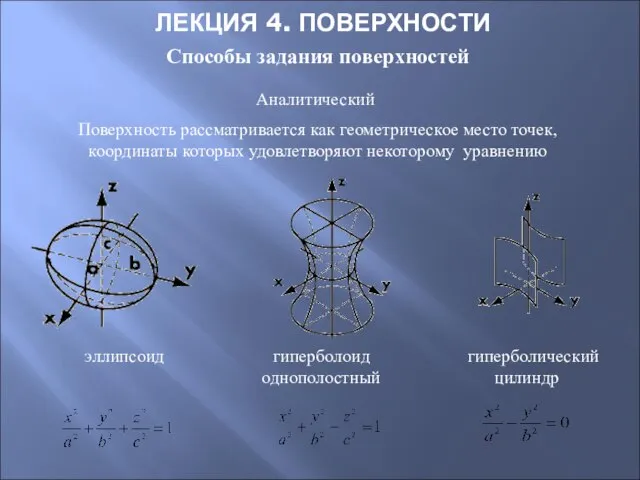
- 32. ЛЕКЦИЯ 4. ПОВЕРХНОСТИ Способы задания поверхностей Аналитический Поверхность рассматривается как геометрическое место точек, координаты которых удовлетворяют
- 33. Кинематический Кинематическую поверхность можно рассматривать как непрерывную совокупность последовательных положений линии, перемещающейся в пространстве по некоторым
- 34. Каркасный Такие поверхности обычно задают достаточно плотной сетью линий и точек, принадлежащих этим поверхностям. Совокупность таких
- 35. КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
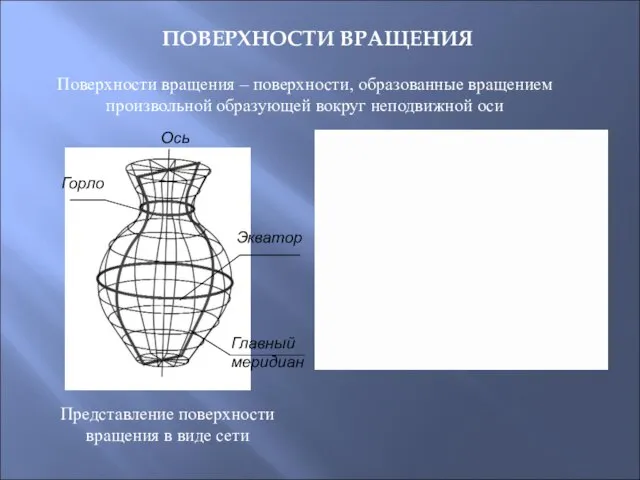
- 36. Поверхности вращения – поверхности, образованные вращением произвольной образующей вокруг неподвижной оси ПОВЕРХНОСТИ ВРАЩЕНИЯ Горло Ось Экватор
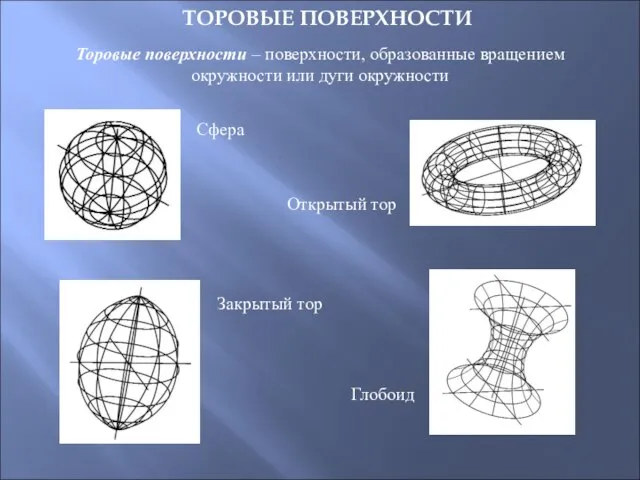
- 37. Торовые поверхности – поверхности, образованные вращением окружности или дуги окружности ТОРОВЫЕ ПОВЕРХНОСТИ Сфера Глобоид Открытый тор
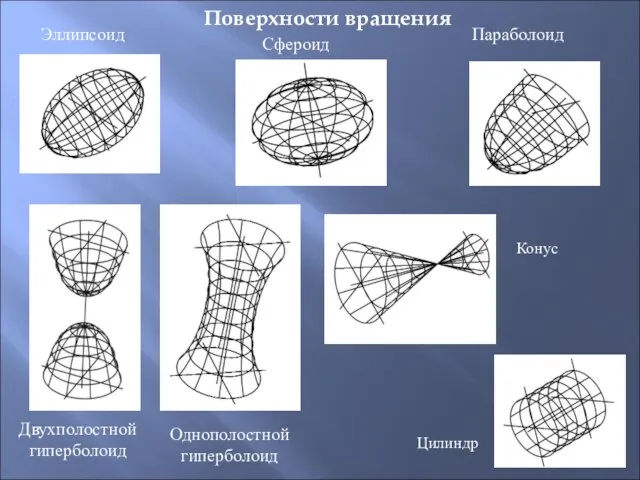
- 38. Поверхности вращения Эллипсоид Двухполостной гиперболоид Сфероид Параболоид Однополостной гиперболоид Конус Цилиндр
- 39. На комплексном чертеже изображается очерк поверхности, а также наиболее важные линии и точки на поверхности ИЗОБРАЖЕНИЕ
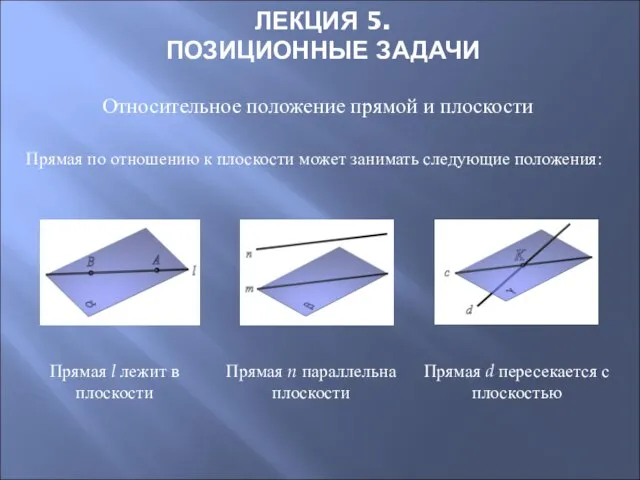
- 40. ЛЕКЦИЯ 5. ПОЗИЦИОННЫЕ ЗАДАЧИ Относительное положение прямой и плоскости Прямая по отношению к плоскости может занимать
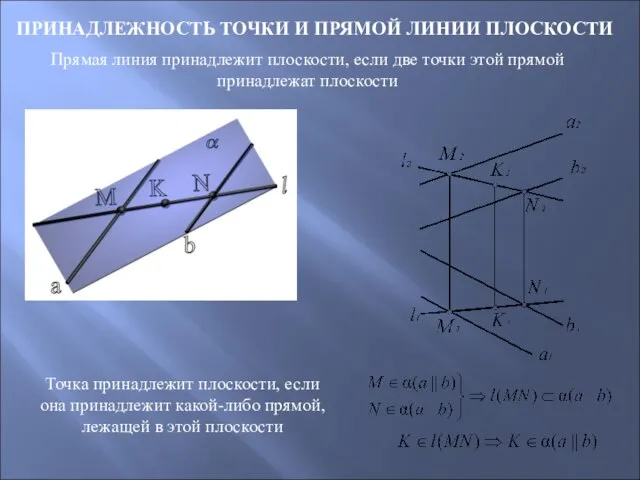
- 41. ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ ЛИНИИ ПЛОСКОСТИ Прямая линия принадлежит плоскости, если две точки этой прямой принадлежат
- 42. ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Прямая параллельна плоскости, если она параллельна какой–либо прямой, лежащей в этой плоскости
- 43. ЛИНИИ УРОВНЯ ПЛОСКОСТИ Прямые, лежащие в данной плоскости и параллельные одной из плоскостей проекций, называются линиями
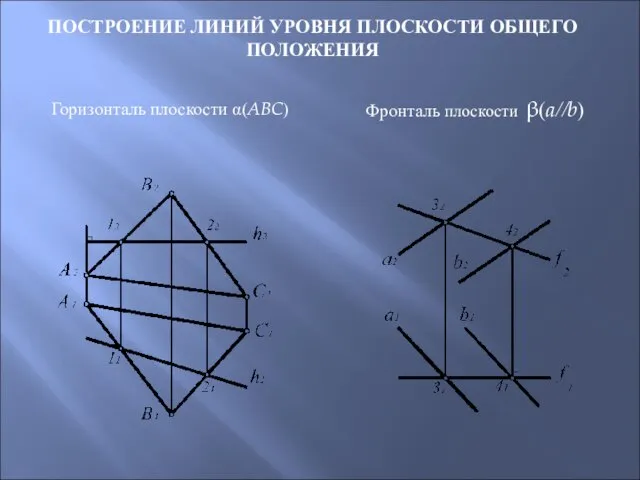
- 44. ПОСТРОЕНИЕ ЛИНИЙ УРОВНЯ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ Горизонталь плоскости α(ABC) Фронталь плоскости β(a//b)
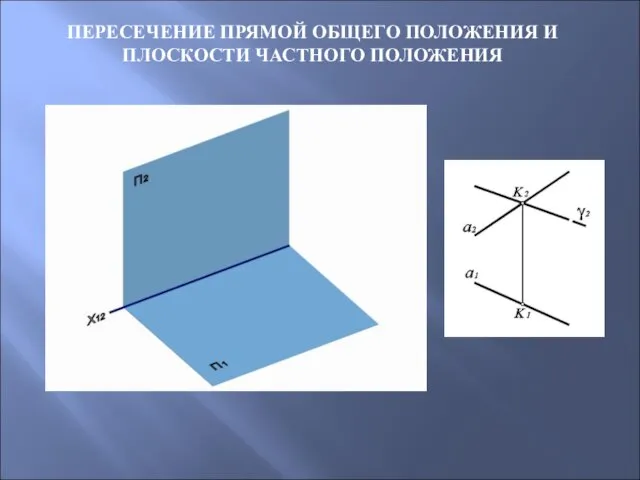
- 45. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ И ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
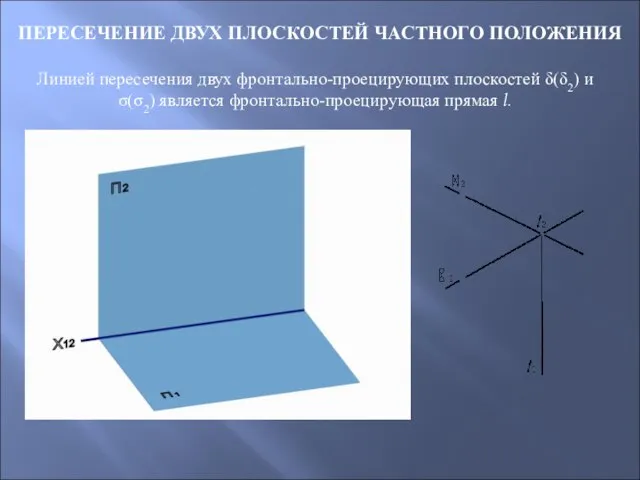
- 46. ПЕРЕСЕЧЕНИЕ ДВУХ ПЛОСКОСТЕЙ ЧАСТНОГО ПОЛОЖЕНИЯ Линией пересечения двух фронтально-проецирующих плоскостей δ(δ2) и σ(σ2) является фронтально-проецирующая прямая
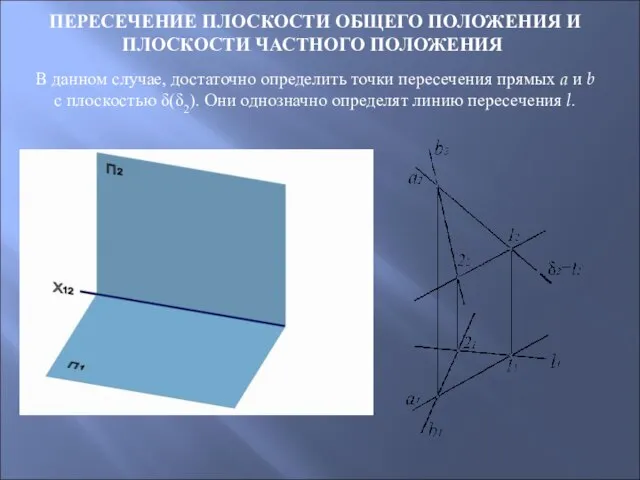
- 47. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ И ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ В данном случае, достаточно определить точки пересечения прямых
- 48. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ И ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ. ПЕРВАЯ ПОЗИЦИОННАЯ ЗАДАЧА Дано: α(ABC) – плоскость общего
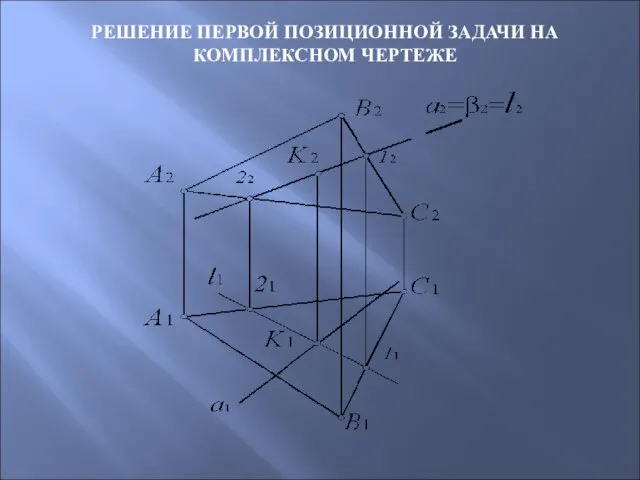
- 49. РЕШЕНИЕ ПЕРВОЙ ПОЗИЦИОННОЙ ЗАДАЧИ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
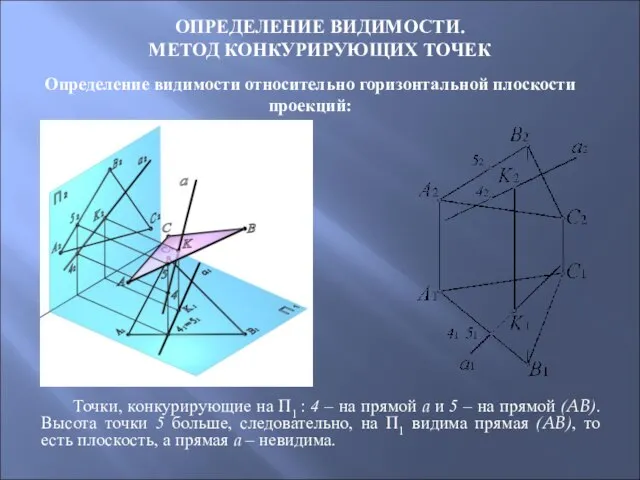
- 50. ОПРЕДЕЛЕНИЕ ВИДИМОСТИ. МЕТОД КОНКУРИРУЮЩИХ ТОЧЕК Определение видимости относительно горизонтальной плоскости проекций: Точки, конкурирующие на П1 :
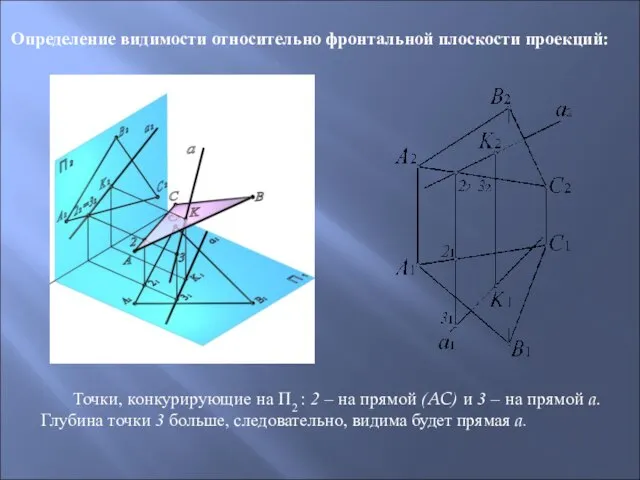
- 51. Определение видимости относительно фронтальной плоскости проекций: Точки, конкурирующие на П2 : 2 – на прямой (AC)
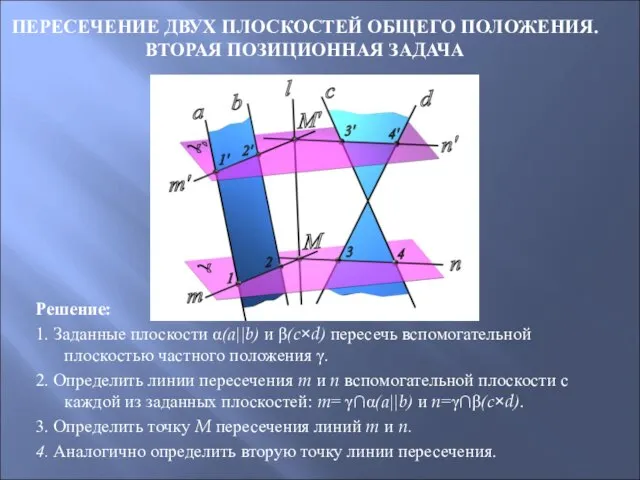
- 52. ПЕРЕСЕЧЕНИЕ ДВУХ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ. ВТОРАЯ ПОЗИЦИОННАЯ ЗАДАЧА Решение: 1. Заданные плоскости α(a||b) и β(c×d) пересечь
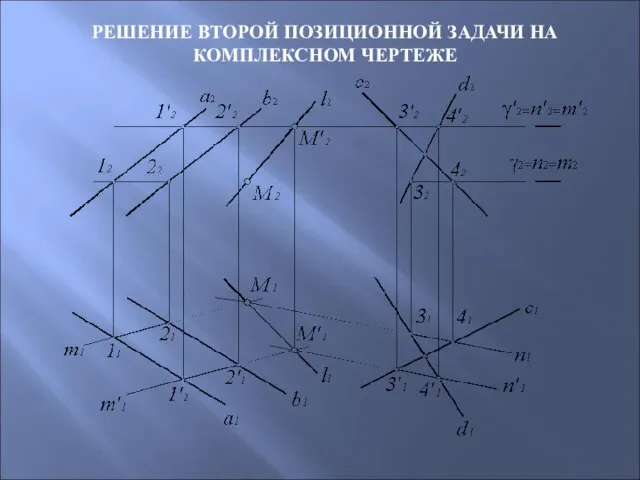
- 53. РЕШЕНИЕ ВТОРОЙ ПОЗИЦИОННОЙ ЗАДАЧИ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
- 54. ЛЕКЦИЯ 6. ТОЧКА НА ПОВЕРХНОСТИ Точка принадлежит поверхности, если она принадлежит какой-либо линии на этой поверхности
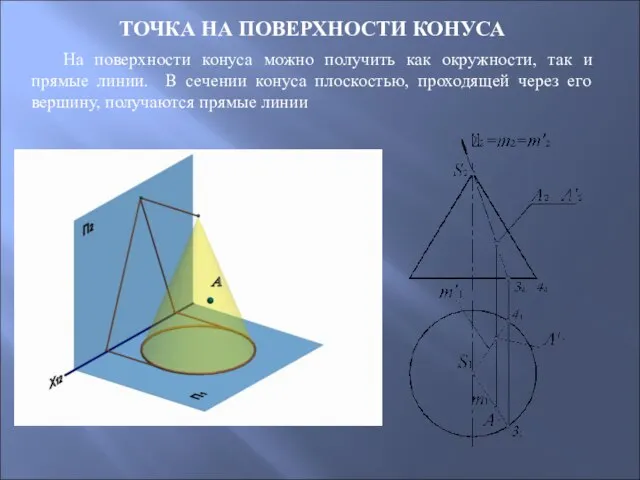
- 55. ТОЧКА НА ПОВЕРХНОСТИ КОНУСА На поверхности конуса можно получить как окружности, так и прямые линии. В
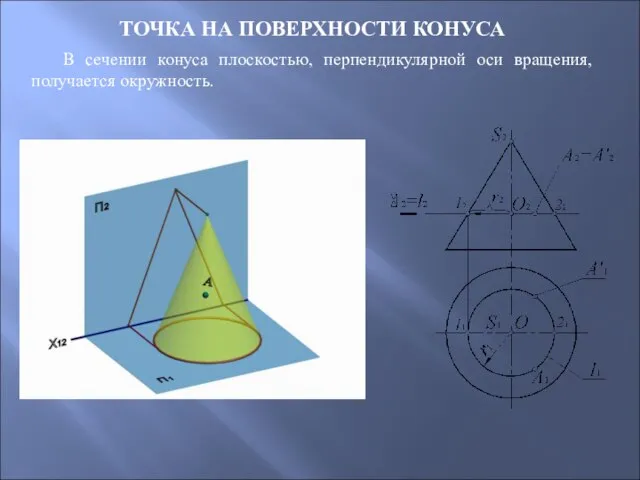
- 56. ТОЧКА НА ПОВЕРХНОСТИ КОНУСА В сечении конуса плоскостью, перпендикулярной оси вращения, получается окружность.
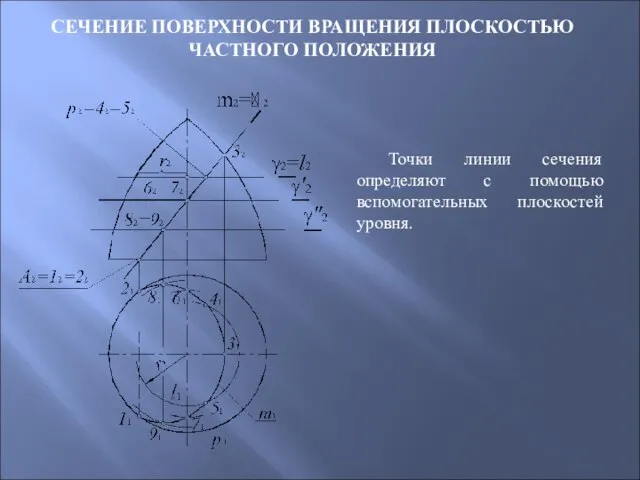
- 57. СЕЧЕНИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ ПЛОСКОСТЬЮ ЧАСТНОГО ПОЛОЖЕНИЯ Точки линии сечения определяют с помощью вспомогательных плоскостей уровня.
- 58. ЦИЛИНДРИЧЕСКИЕ СЕЧЕНИЯ В сечении цилиндра плоскостью, перпендикулярной оси вращения, получается окружность.
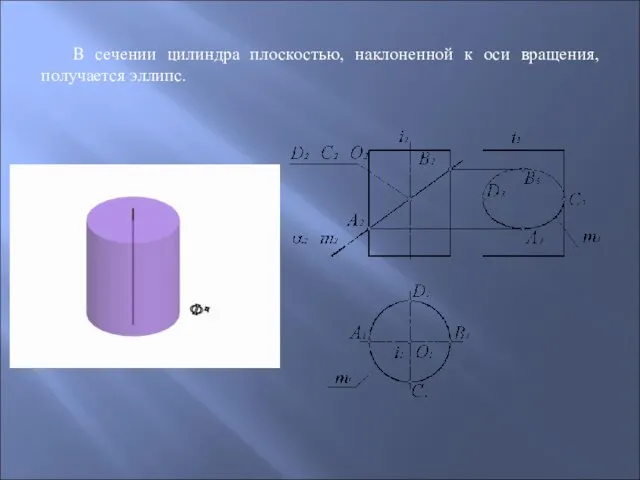
- 59. В сечении цилиндра плоскостью, наклоненной к оси вращения, получается эллипс.
- 60. В сечении цилиндра плоскостью, параллельной оси вращения, получаются параллельные прямые.
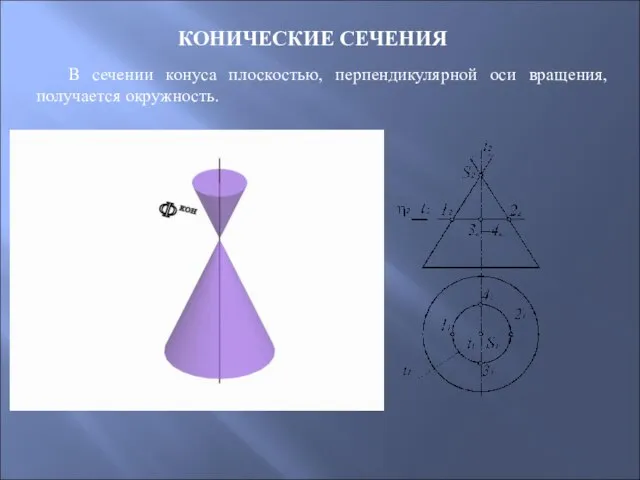
- 61. КОНИЧЕСКИЕ СЕЧЕНИЯ В сечении конуса плоскостью, перпендикулярной оси вращения, получается окружность.
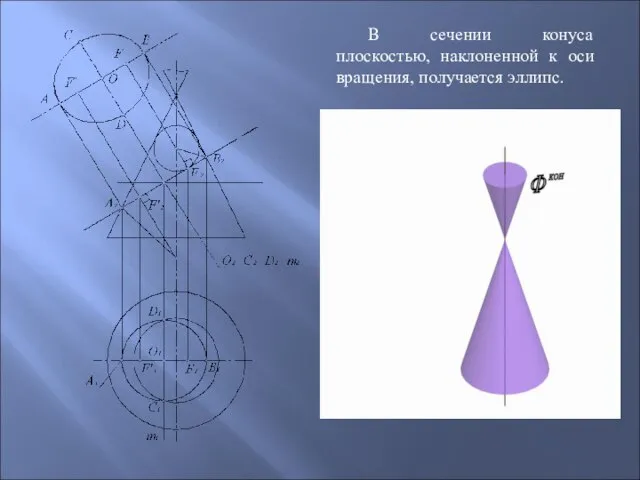
- 62. В сечении конуса плоскостью, наклоненной к оси вращения, получается эллипс.
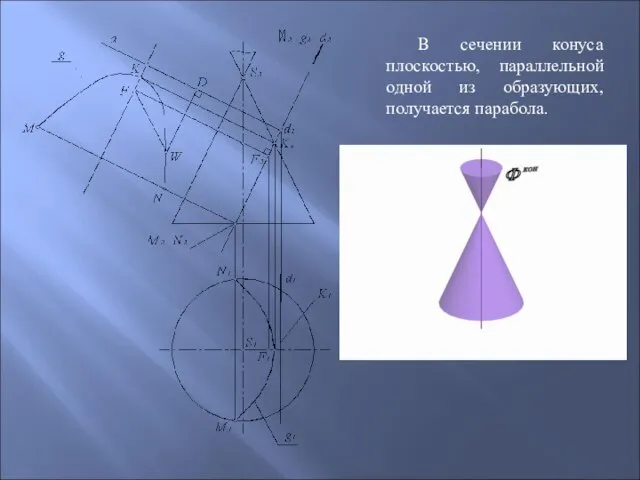
- 63. В сечении конуса плоскостью, параллельной одной из образующих, получается парабола.
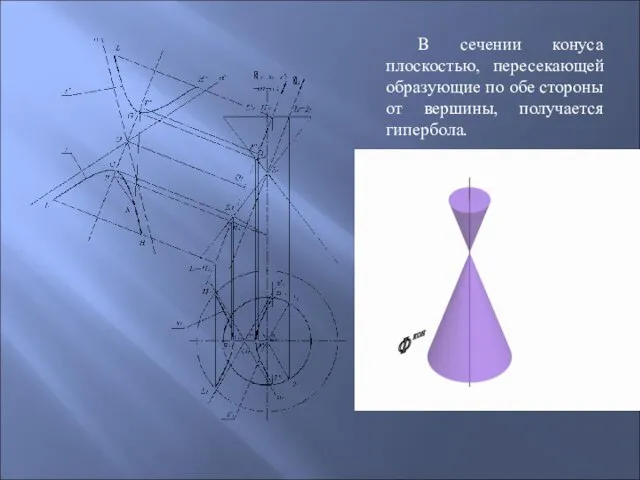
- 64. В сечении конуса плоскостью, пересекающей образующие по обе стороны от вершины, получается гипербола.
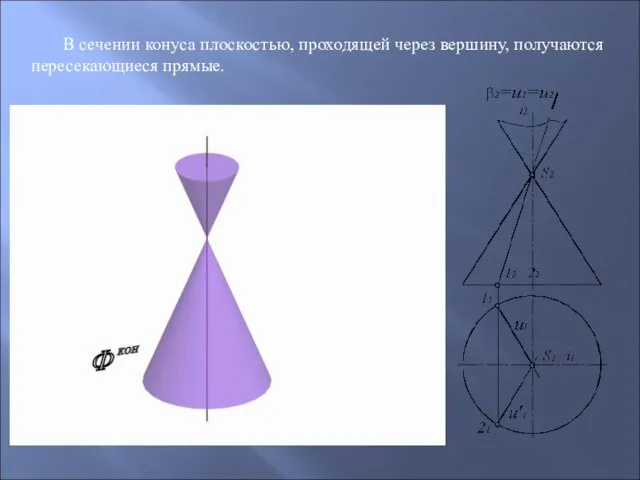
- 65. В сечении конуса плоскостью, проходящей через вершину, получаются пересекающиеся прямые.
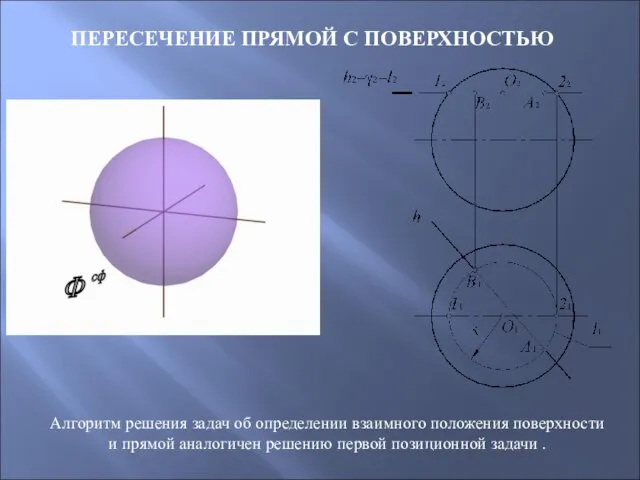
- 66. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПОВЕРХНОСТЬЮ Алгоритм решения задач об определении взаимного положения поверхности и прямой аналогичен решению
- 67. ЛЕКЦИЯ 7. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ 1. Обе заданные поверхности Ф' и Ф “ рассекают третьей, вспомогательной плоскостью
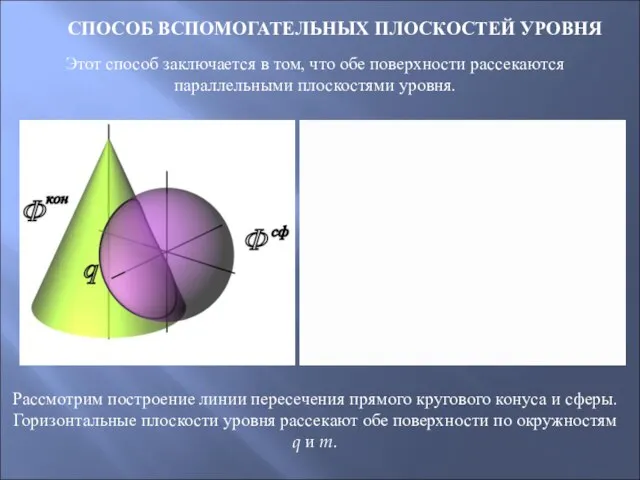
- 68. СПОСОБ ВСПОМОГАТЕЛЬНЫХ ПЛОСКОСТЕЙ УРОВНЯ Этот способ заключается в том, что обе поверхности рассекаются параллельными плоскостями уровня.
- 69. Построение линии пересечения поверхностей способом вспомогательных плоскостей уровня на комплексном чертеже
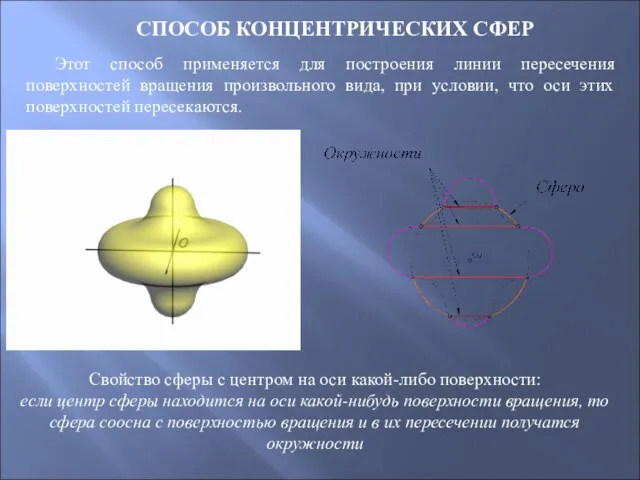
- 70. СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР Этот способ применяется для построения линии пересечения поверхностей вращения произвольного вида, при условии,
- 71. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ С ПЕРЕСЕКАЮЩИМИСЯ ОСЯМИ Точка пересечения осей поверхностей принимается за центр вспомогательных
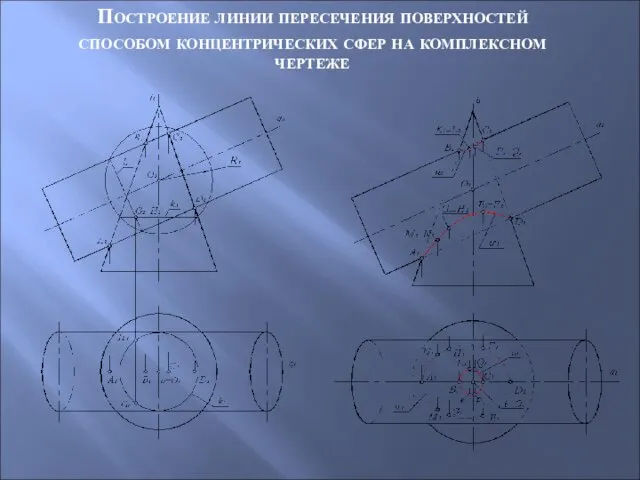
- 72. Построение линии пересечения поверхностей способом концентрических сфер на комплексном чертеже
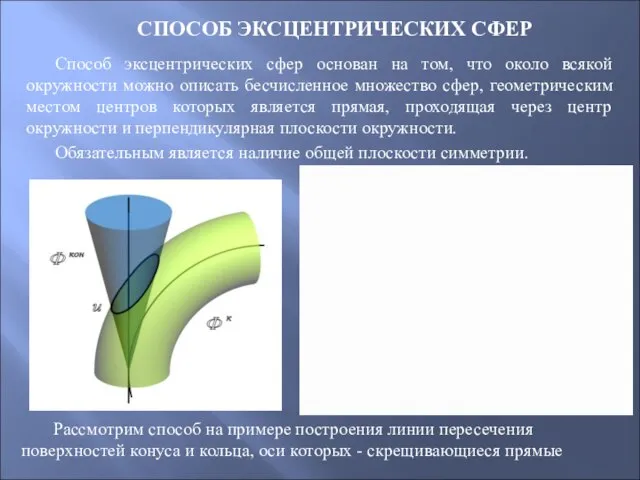
- 73. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР Способ эксцентрических сфер основан на том, что около всякой окружности можно описать бесчисленное
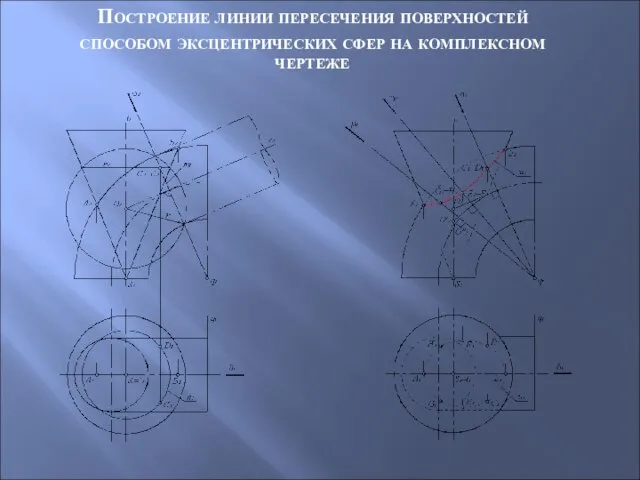
- 74. Построение линии пересечения поверхностей способом эксцентрических сфер на комплексном чертеже
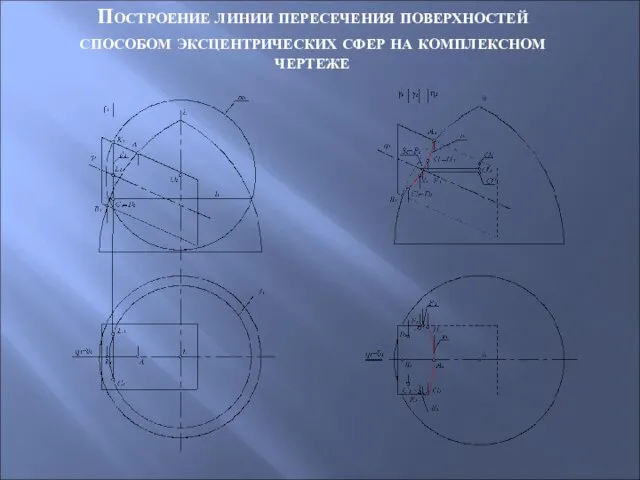
- 75. Рассмотрим также способ эксцентрических сфер на примере построения линии пересечения поверхности тора и наклонного (эллиптического) цилиндра.
- 76. Построение линии пересечения поверхностей способом эксцентрических сфер на комплексном чертеже
- 77. ЛЕКЦИЯ 8. МЕТРИЧЕСКИЕ ЗАДАЧИ Задачи, в которых определяются различные геометрические величины – расстояния между объектами, длины
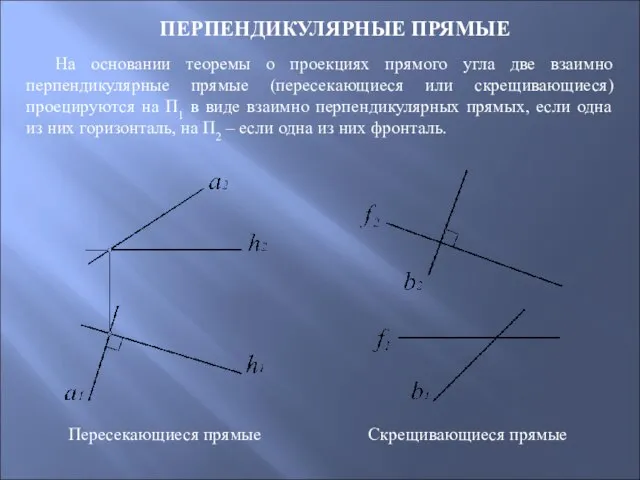
- 78. ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ На основании теоремы о проекциях прямого угла две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся)
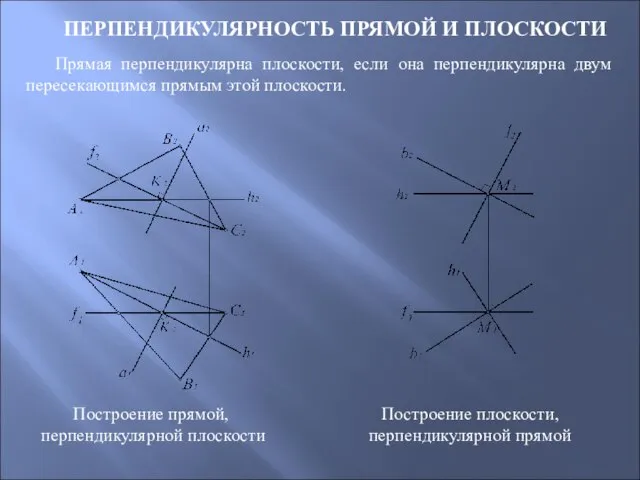
- 79. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. Построение
- 80. ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
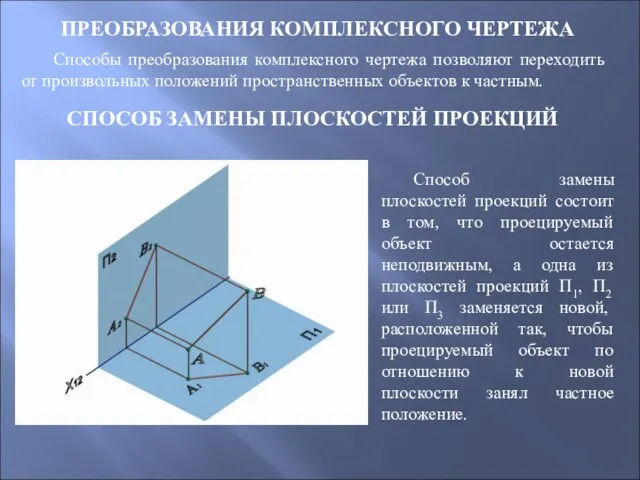
- 81. ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА Способы преобразования комплексного чертежа позволяют переходить от произвольных положений пространственных объектов к частным.
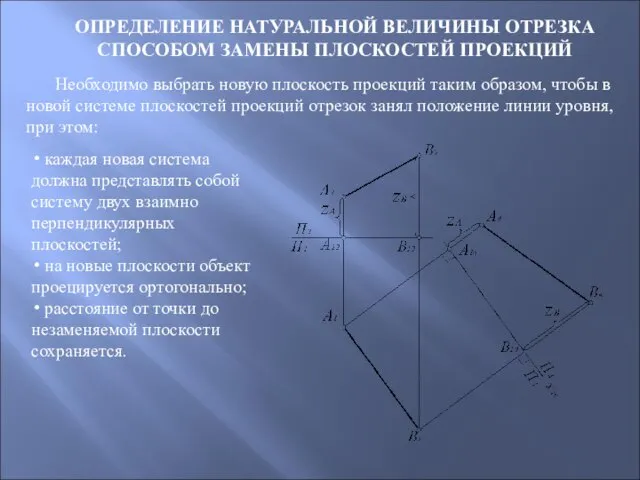
- 82. ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ОТРЕЗКА СПОСОБОМ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ Необходимо выбрать новую плоскость проекций таким образом, чтобы
- 83. СПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ Плоскопараллельным движением объекта в пространстве называется такое его перемещение, при котором все точки
- 84. ПРИМЕНЕНИЕ СПОСОБА ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ Рассмотрим преобразование отрезка [AB] общего положения в положение фронтальной линии уровня, а
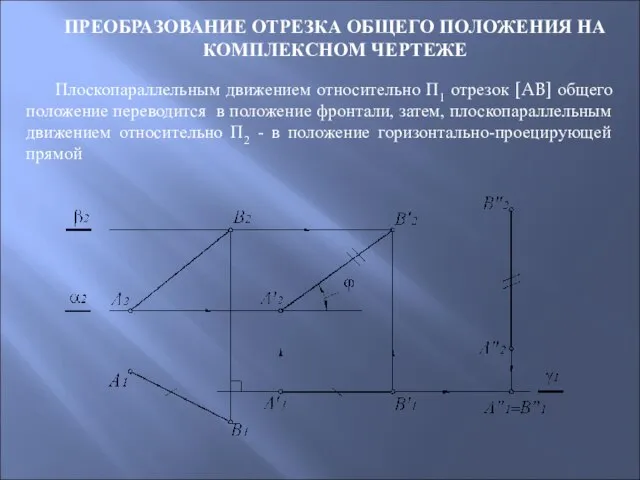
- 85. ПРЕОБРАЗОВАНИЕ ОТРЕЗКА ОБЩЕГО ПОЛОЖЕНИЯ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ Плоскопараллельным движением относительно П1 отрезок [AB] общего положение переводится
- 86. ВРАЩЕНИЕ Вращение – это движение по окружности вокруг некоторой оси. При преобразовании комплексного чертежа способом вращения
- 87. ВРАЩЕНИЕ ВОКРУГ ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ При вращении вокруг горизонтально-проецирующей прямой A1 перемещается по окружности l1 с центром
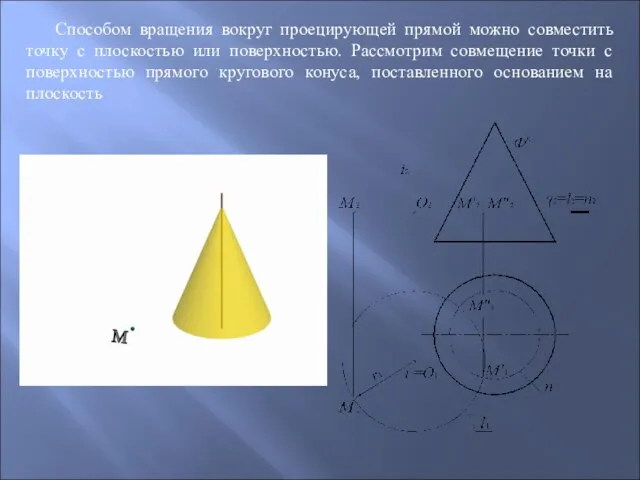
- 88. Способом вращения вокруг проецирующей прямой можно совместить точку с плоскостью или поверхностью. Рассмотрим совмещение точки с
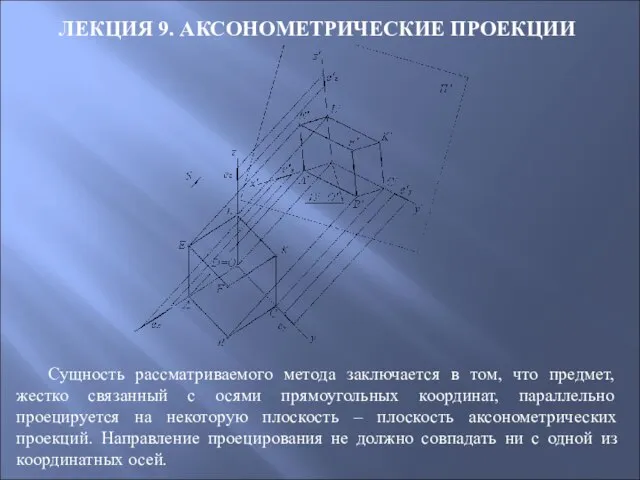
- 89. ЛЕКЦИЯ 9. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ Сущность рассматриваемого метода заключается в том, что предмет, жестко связанный с осями
- 90. ВИДЫ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ Показателем искажения называют отношение аксонометрического масштаба к соответствующему натуральному: по оси x: u=ex'/ex;
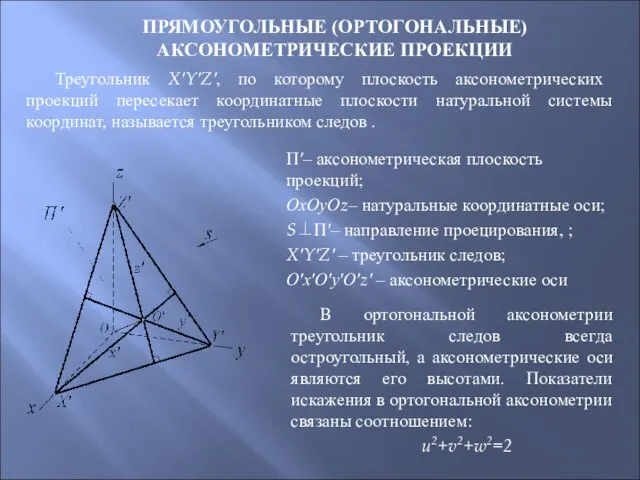
- 91. ПРЯМОУГОЛЬНЫЕ (ОРТОГОНАЛЬНЫЕ) АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ Треугольник X′Y′Z′, по которому плоскость аксонометрических проекций пересекает координатные плоскости натуральной системы
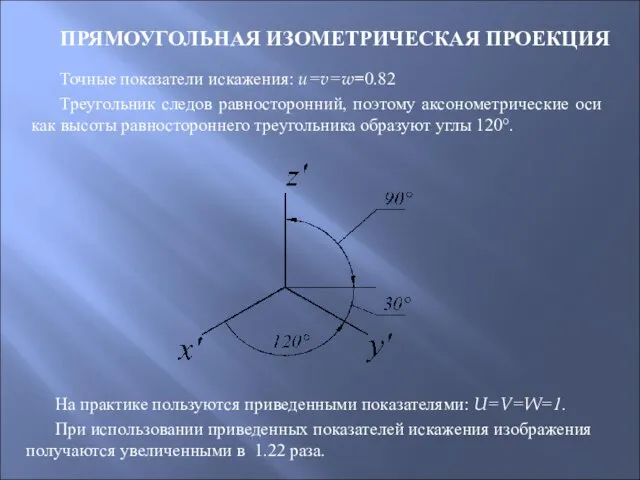
- 92. ПРЯМОУГОЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ Точные показатели искажения: u=v=w=0.82 Треугольник следов равносторонний, поэтому аксонометрические оси как высоты равностороннего
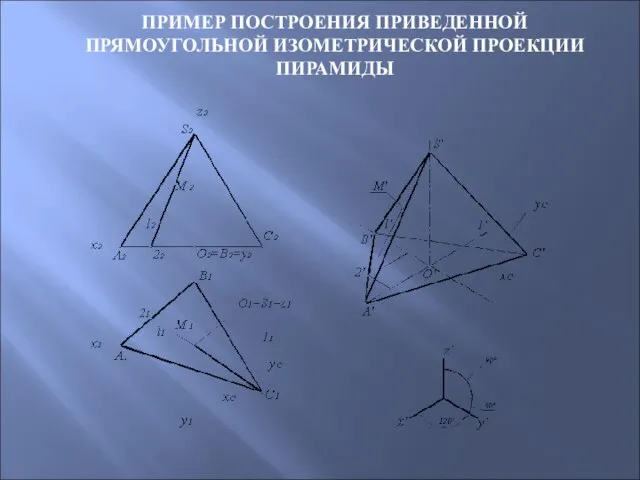
- 93. ПРИМЕР ПОСТРОЕНИЯ ПРИВЕДЕННОЙ ПРЯМОУГОЛЬНОЙ ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ ПИРАМИДЫ
- 94. ПРЯМОУГОЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ Точные показатели искажения: u=w=0.94; v=0.47. На практике пользуются приведенными показателями:. U=W=1; V=0.5.
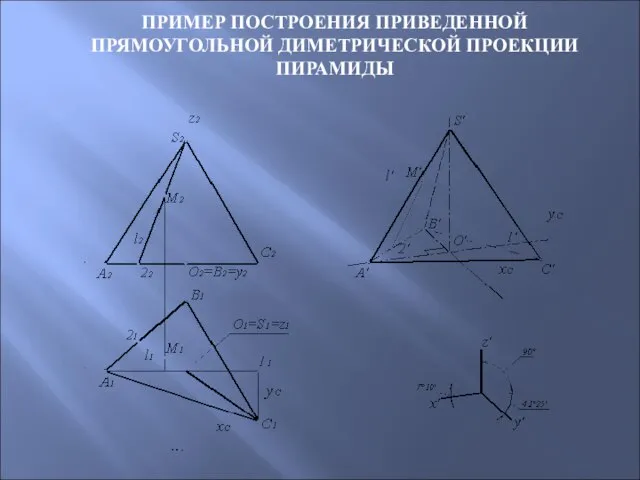
- 95. ПРИМЕР ПОСТРОЕНИЯ ПРИВЕДЕННОЙ ПРЯМОУГОЛЬНОЙ ДИМЕТРИЧЕСКОЙ ПРОЕКЦИИ ПИРАМИДЫ
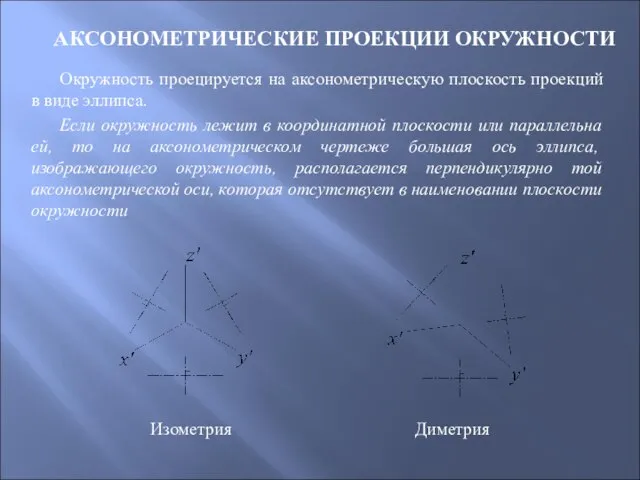
- 96. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ОКРУЖНОСТИ Окружность проецируется на аксонометрическую плоскость проекций в виде эллипса. Если окружность лежит в
- 97. РАЗМЕРЫ ОСЕЙ ЭЛЛИПСА В ПРЯМОУГОЛЬНЫХ ПРИВЕДЕННЫХ ИЗОМЕТРИИ И ДИМЕТРИИ (d – ДИАМЕТР ОКРУЖНОСТИ). А′В′=1,22d – большая
- 99. Скачать презентацию


























![ПРИМЕНЕНИЕ СПОСОБА ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ Рассмотрим преобразование отрезка [AB] общего положения в положение](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/876572/slide-83.jpg)





 ВодорастворимыеРастительныеМасла (ВРМ)
ВодорастворимыеРастительныеМасла (ВРМ) Областные особенности русского костюма
Областные особенности русского костюма Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация
Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация Панели стеновые CPL
Панели стеновые CPL Подготовка к ЕГЭ. Решение задач на движение
Подготовка к ЕГЭ. Решение задач на движение Презентация замороженных фруктовых пюре и ягод Dira
Презентация замороженных фруктовых пюре и ягод Dira Зеленый наряд нашего города
Зеленый наряд нашего города Техника квиллинг
Техника квиллинг «Атлас флоры и фауны Белого моря» это коллективная монография, подготовленная большой группой специалистов. Книга дает возможнос
«Атлас флоры и фауны Белого моря» это коллективная монография, подготовленная большой группой специалистов. Книга дает возможнос Текхнология блокчейн: инвестиции в будущее
Текхнология блокчейн: инвестиции в будущее Выгода открытия бизнеса в 2020 году
Выгода открытия бизнеса в 2020 году Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word
Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word Романтизм в русской живописи XIX века
Романтизм в русской живописи XIX века Развитие методов синтеза, исследование физико-химических и электрофизических свойств модифицированных наноуглеродных и фторугл
Развитие методов синтеза, исследование физико-химических и электрофизических свойств модифицированных наноуглеродных и фторугл Профи-digest
Профи-digest lecture_5
lecture_5 Виды сказуемых
Виды сказуемых Radiographic Interpretation of Infections of Jaws
Radiographic Interpretation of Infections of Jaws phpm2fa0e_ovosibirskaya-oblast
phpm2fa0e_ovosibirskaya-oblast Итоги 2-й четверти
Итоги 2-й четверти Математика-царица наук?
Математика-царица наук? Экономический смысл налогообложения
Экономический смысл налогообложения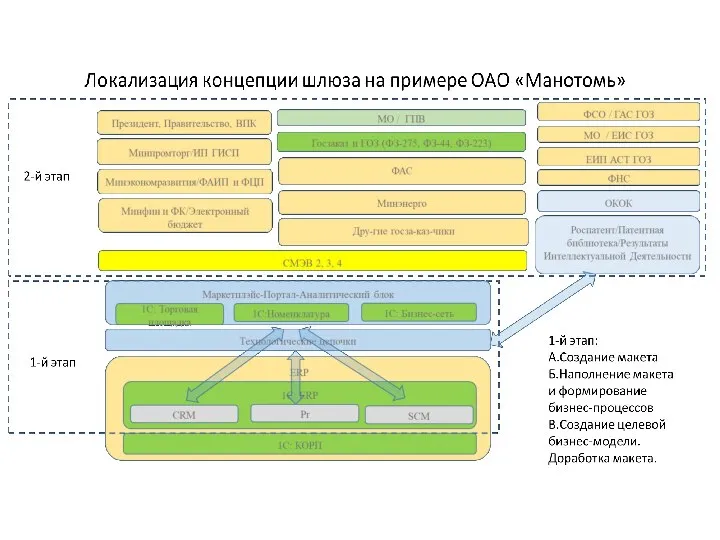 Локализация концепции шлюза на примере ОАО Манотомь
Локализация концепции шлюза на примере ОАО Манотомь Презентация на тему Справедливость и равенство
Презентация на тему Справедливость и равенство Protection of environment
Protection of environment Статусы пассажиров. Служебные пассажиры
Статусы пассажиров. Служебные пассажиры Буквы Ч и Щ в суффиксах имён существительных
Буквы Ч и Щ в суффиксах имён существительных Отдыхаем на отлично
Отдыхаем на отлично