Наибольшее и наименьшее значение

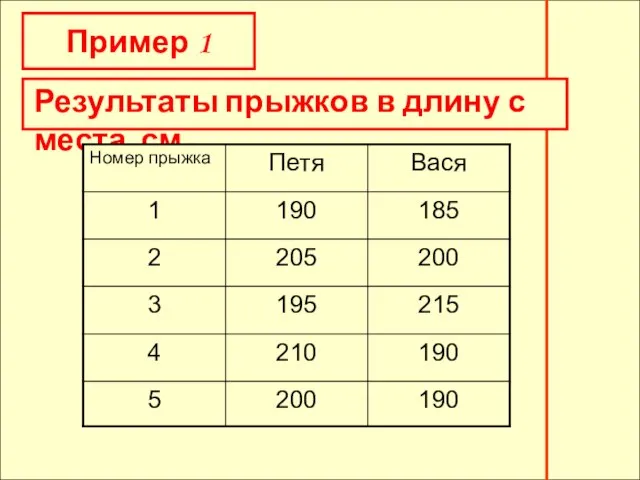
Результаты прыжков в длину с места, см
Результаты прыжков в длину с места, см
Пример 1

Определение
Определение
Разность между наибольшим и наименьшим числом называется размахом набора чисел.
Таблица Производство пшеницы в России
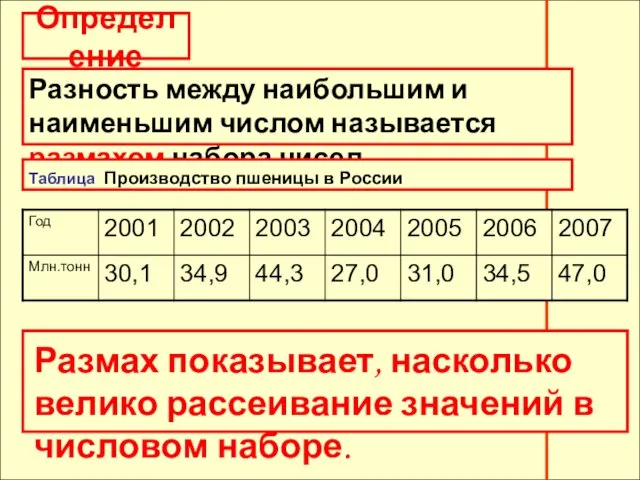
Размах показывает, насколько велико рассеивание значений в числовом наборе.

При изучении учебной нагрузки учащихся выделили группу из 12 девятиклассников. Их попросили отметить в определенный день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.
При изучении учебной нагрузки учащихся выделили группу из 12 девятиклассников. Их попросили отметить в определенный день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.
27 – среднее значение
Наибольшее значение – 37; наименьшее значение – 18;
Размах ряда равен
37 – 18 = 19

При анализе сведений о времени, затраченном девятиклассниками на выполнение домашнего задания по алгебре, нас могут интересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели. Интересно, например, знать, какой расход времени является типичным для выделенной группы учащихся, то есть какое число встречается в ряду данных чаще всего. Нетрудно заметить, что таким числом является число 25. Говорят, что число 25 – мода рассматриваемого ряда.
При анализе сведений о времени, затраченном девятиклассниками на выполнение домашнего задания по алгебре, нас могут интересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели. Интересно, например, знать, какой расход времени является типичным для выделенной группы учащихся, то есть какое число встречается в ряду данных чаще всего. Нетрудно заметить, что таким числом является число 25. Говорят, что число 25 – мода рассматриваемого ряда.
Модой ряда чисел называется число, чаще других встречающееся в данном ряду.
Ряд чисел может иметь более одной моды или не иметь моды совсем.

Рассмотрим еще пример. Пусть, проведя учет деталей, изготовленных за смену рабочими одной бригады, получили такой ряд данных:
36, 35, 35, 36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38, 36, 39, 36.
Рассмотрим еще пример. Пусть, проведя учет деталей, изготовленных за смену рабочими одной бригады, получили такой ряд данных:
36, 35, 35, 36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38, 36, 39, 36.
Найдем для него среднее арифметическое, размах и моду. Для этого удобно предварительно составить из полученных данных упорядоченный ряд чисел, т. е. такой ряд, в котором каждое последующее число не меньше (или не больше) предыдущего. Получим:
35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 38, 38, 38, 39, 39, 39, 39.
Вычислим среднее арифметическое:
Размах ряда равен . Мода данного ряда равна 36, так как число 36 чаще всего встречается в этом ряду.

Например, в ряду чисел
47, 46, 50, 52, 47, 52, 49, 45, 43, 53
две моды – это числа 47 и 52,
а в ряду чисел 69, 68, 66, 80, 67, 65, 71, 74, 63, 73, 72
моды нет.
Например, в ряду чисел
47, 46, 50, 52, 47, 52, 49, 45, 43, 53
две моды – это числа 47 и 52,
а в ряду чисел 69, 68, 66, 80, 67, 65, 71, 74, 63, 73, 72
моды нет.
Моду ряда данных обычно находят тогда, когда хотят выявить некоторый типичный показатель. Например, если изучаются данные о размерах мужских сорочек, проданных в определенный день в универмаге, то удобно воспользоваться таким показателем, как мода, который характеризует размер, пользующийся наибольшим спросом. Находить в этом случае среднее арифметическое не имеет смысла. Мода является наиболее приемлемым показателем при выявлении, например, расфасовки некоторого товара, которой отдают предпочтение покупатели; цены на товар данного вида, наиболее распространенной на рынке, и т. п.