Назначение геометрических преобразований

Цель курса
Изучение основных правил и требований к порядку разработки, оформления и обращения конструкторской документации

Геометрический язык
По С.А. Фролову геометрический язык состоит из обозначений и символов, принятых в курсе математики :
- обозначения геометрических фигур и отношений между ними;
обозначения логических операций.
Особое внимание необходимо уделять символам, которые применяются для обозначения проекций геометрических фигур.

Основные понятия и определения
Плоскостью называется поверхность, образуемая движением примой линии, которая движется параллельно самой себе на неподвижной направляющей.
Поверхность – множество последовательных положений движущейся линии

Обозначение геометрических фигур
Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами латинского алфавита или
арабскими цифрами:
(курсив) А, В, С, D, ..., L, M, N, ..
(прямой шрифт) 1,2, 3,4,..., 12, 13, 14,...

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
а, b, с, d, l, m, n, ...
Линии уровня обозначаются:
h — горизонталь;
f — фронталь.
Для прямых используются также следующие обозначения:
(AB) — прямая, проходящая через точки А и В;
[AB) - луч с началом в точке А;
[AB] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:
α — альфа, β — бэта, — γ гамма, σ — cигма, …, ξ— кси, η — эта, ν – ню (ни), …
Чтобы подчеркнуть способ задания поверхности, следует указывать
геометрические элементы, которыми она определяется, например:
α (а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:
ABC — угол с вершиной в точке В, а также a°, β°,..., φ°, ...
6. Угловая величина (градусная мера) обозначается знаком , который
ставится над углом:
ABC — величина угла ABC,
φ° — величина угла φ.
Прямой угол отмечается квадратом с точкой внутри .

7. Расстояния между геометрическими фигурами обозначаются двумя
вертикальными отрезками — | | .
Например:
|АВ| — расстояние между точками А и В (длина отрезка AB);
|Аа| — расстояние от точки А до линии а;
|Аα|— расстояние от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| — расстояние между поверхностями α и β.

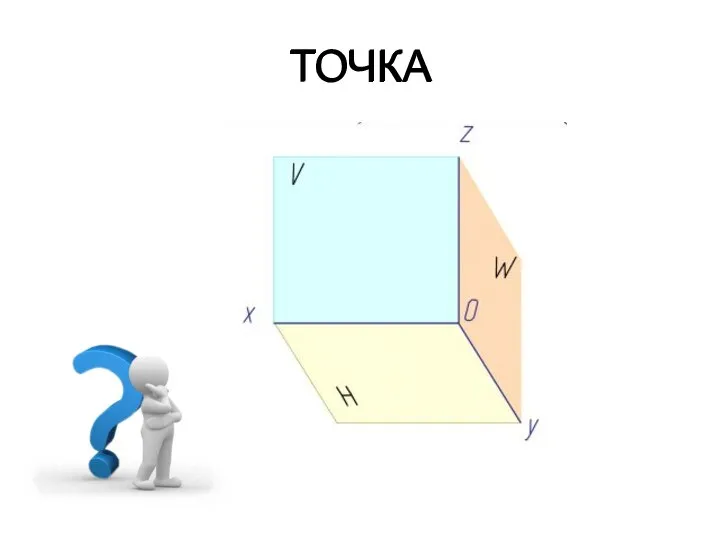
8. Для плоскостей проекций приняты обозначения:π1, и π2,
где π1 — горизонтальная плоскость проекций;
π2 — фронтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т.д.

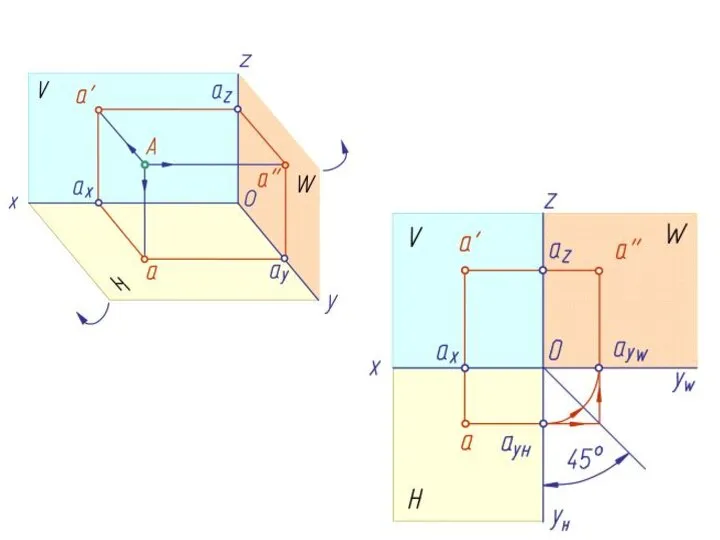
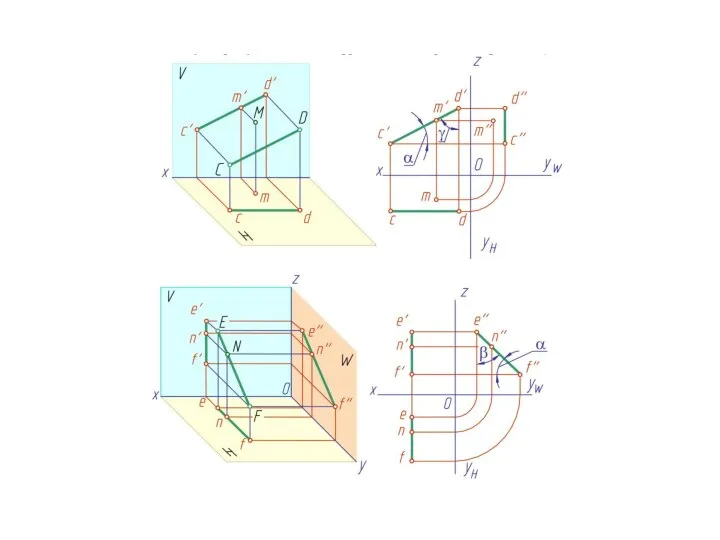
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции,
на которой они получены:
A', B', C', D', ..., L', M', N', ... — горизонтальные проекции точек;
А", В", С", D", ..., L", M", N", ... — фронтальные проекции точек;
a', b', c', d', ...,l, m', n', ... — горизонтальные проекции линий;
а", b", с", d",...,l, m", n", ... — фронтальные проекции линий;
α', β', γ', δ', ..., ζ', η', ν', ... — горизонтальные проекции поверхностей;
α", β", γ", δ", ..., ζ", η", ν",... — фронтальные проекции поверхностей.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: На — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии) а.

11. Следы плоскостей (поверхностей) обозначаются теми же буквами,
что и горизонталь или фронталь, с добавлением подстрочного индекса 0α,
подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
Так: h0а — горизонтальный след плоскости (поверхности) α;
f0а — фронтальный след плоскости (поверхности) α.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1, 2, 3, … , n:
А1, А2,А3, …, Аn;
а1, а2,а3, … ,аn –последовательность линий
α1, α2, α3,..., αn;- последовательность поверхностей
Ф1, Ф2, Ф3,..., Фn – последовательность фигур
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
A0, B0, С0, D0, ...

Аксонометрические проекции
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :
A0,B0, C0, D0, ...
1°, 2°, 3°, 4°,...
a0, b0,c0,d0 … ;
α0, β0, γ0,δ0,... ;

Вторичные проекции точек в аксонометрических проекциях обозначаются путем добавления верхнего индекса 1:
А10, В10, С10, D10,...
110, 210, 310, 410,...
a10, b10 , с10, d10,...
α10, β 10, γ 10, δ 10,...

СВОЙСТВА ЕВКЛИДОВА ПРОСТРАНСТВА
С позиции теории множеств геометрическая фигура есть не пустое множество.
Точки, прямые и плоскости евклидова пространства находятся в определенном взаимоотношении, которое может быть обозначено словом принадлежность или инцидентность.
Термин «инцидентность» заменяет такие понятия, как «лежать на», «проходить через».

Вместо выражений «точка А лежит на плоскости а», «прямая а проходит через точку В» можно употреблять выражения «точка А инцидентна (принадлежит) плоскости а», «точка В инцидентна (принадлежит) прямой а».
В символической форме эти выражения можно записать А ∈ α; В ∈ а.

Отношения принадлежности между элементами евклидова пространства могут быть выражены следующими предложениями.
1. Если точка А принадлежит прямой а, а прямая а принадлежит плоскости α, то точка А принадлежит плоскости α:
А ∈ а ⊂ α ⇒ А ∈α .

2. Две различные точки А и В всегда принадлежат одной и той же и только одной прямой а или каждой прямой а принадлежат, по крайней
мере, две точки А и В:
∀(A, В) (А ≠ В) ⇒(∃1a) ∍ (А, В).
Три различные точки А, В и С, не принадлежащие одной прямой, принадлежат одной и той же и только одной плоскости:
(∀А, В,С)(A ≠ В ≠ С) ∧ (А, В, С∉ а) ⇒ (∃1α a)(α э А, В, С).

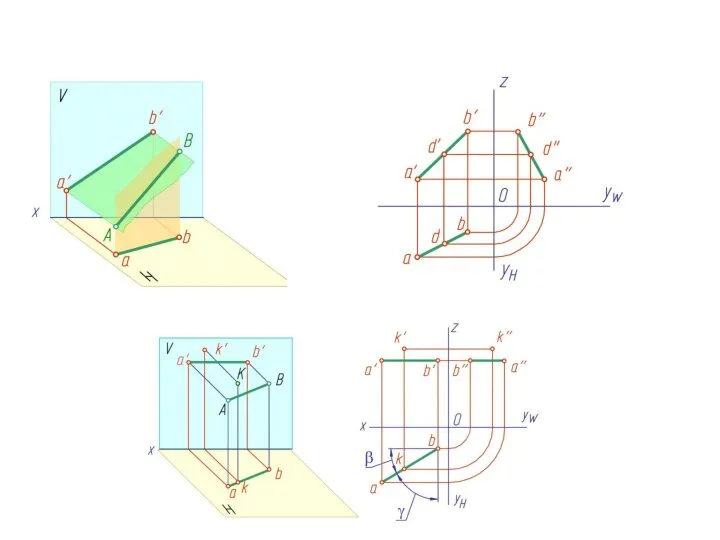
4. Если две точки А и В, принадлежащие прямой а, принадлежат плоскости α, то прямая а принадлежит плоскости α:
(∀А, B)(A ≠ B)(A, В а) ∧ (А, В ∈α) ⇒ (а⊂ α).
Кроме приведенных выше, могут быть сформулированы и другие предложения принадлежности для элементов евклидова пространства. К таким предложениям, в частности, относятся:

5. Две прямые, принадлежащие одной плоскости, могут принадлежать одной точке, но этого может и не быть.
6. Две плоскости могут принадлежать одной и той же прямой, но этого может и не быть.
7. Плоскость и не принадлежащая ей прямая могут принадлежать одной точке, но этого может и не быть.
Последние три предложения по существу перефразируют аксиому о параллельности.

Предложение 5 утверждает, что в евклидовой плоскости две прямые либо пересекаются (принадлежат одной точке), либо не имеют общей точки — в этом случае они называются параллельными. Аналогично предложение 6 говорит о том, что в евклидовом пространстве две плоскости либо пересекаются (принадлежат одной прямой) либо они параллельны, а предложение 7 - о том, что прямая, не принадлежащая плоскости, либо пересекает ее (прямая и плоскость принадлежат одной точке), либо они параллельны.

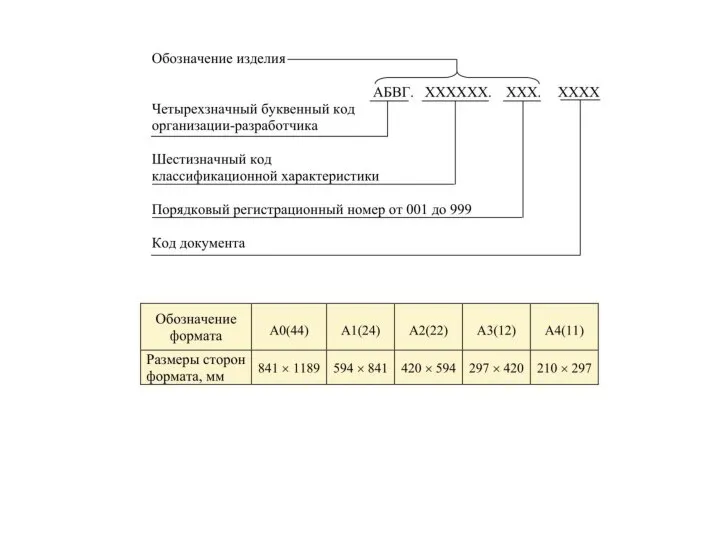
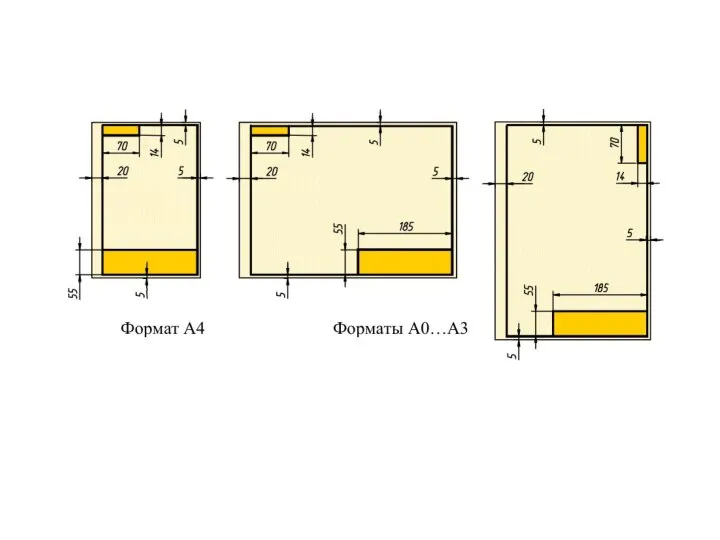
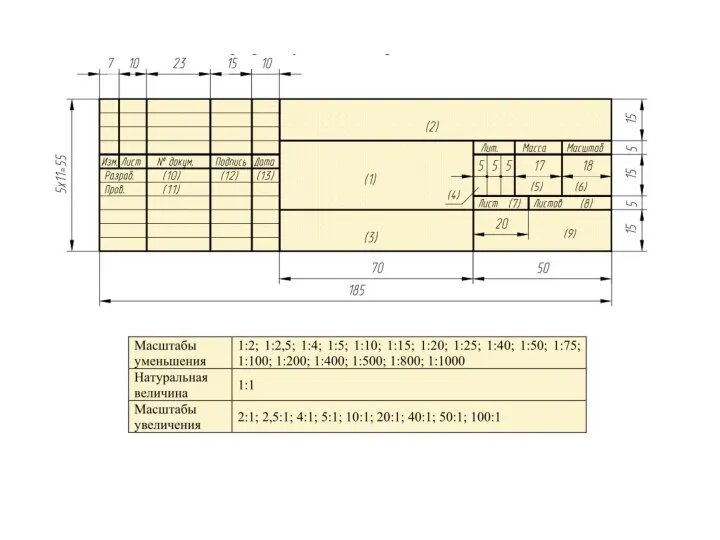
Этапы конструирования, изготовления и реализации изделия
превратить физическую или мысленную модель изделия в графическую;
графическую модель описать аналитически;
выполнить численный анализ изделия на конструкторскую и экономическую обосно-ванность графической модели изделия.
разработать математическую модель управления процессом разработки изделия, модификации и реализации.

ПЕРЕРЫВ

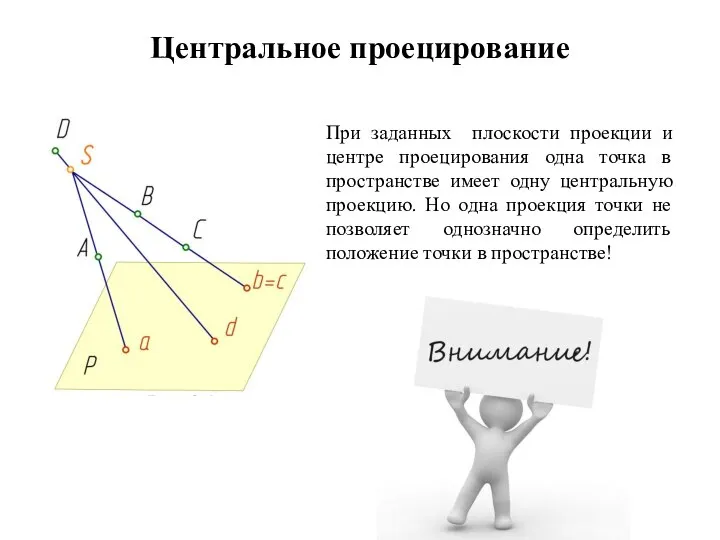
Центральное проецирование
При заданных плоскости проекции и центре проецирования одна точка в пространстве имеет одну центральную проекцию. Но одна проекция точки не позволяет однозначно определить положение точки в пространстве!

Центральное проецирование

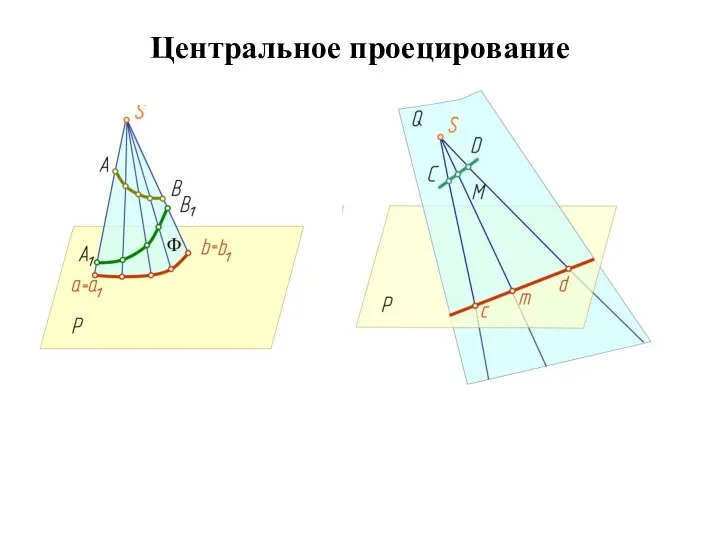
Основные свойства центрального проецирования
Точка проецируется в точку;
Прямая, не проходящая через центр проецирования, проецируется в прямую (иначе в точку);
Плоская фигура не принадлежащая проецирующей плоскости, проецируется в двумерную фигуру (иначе в прямую линию).
Трехмерная фигура проецируется в двумерную.

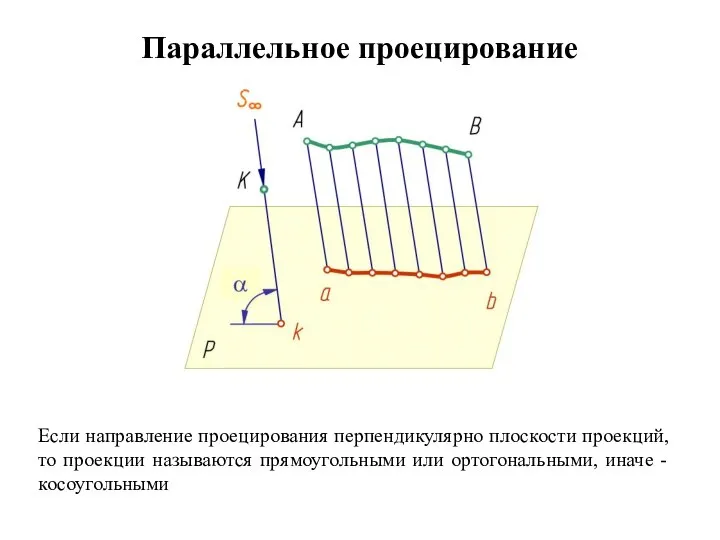
Параллельное проецирование
Если направление проецирования перпендикулярно плоскости проекций, то проекции называются прямоугольными или ортогональными, иначе - косоугольными

Основные свойства параллельного проецирования
Точка проецируется в точку;
Прямая проецируется в прямую;
Если точка принадлежит линии, то проекция этой точки принадлежит проекции линии (свойство принадлежности).
Если отрезок прямой делится точкой в некотором отношении, то проекция отрезка делится проекцией этой точки в том же отношении.

Основные свойства параллельного проецирования
Параллельные проекции взаимно параллельных прямых параллельны, о отношение длин отрезков этих прямых равно отношению длин их проекций;
Плоская фигура, параллельная плоскости проекций, проецируется на эту же плоскость в такую же фигуру;
Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида или размеров проекций.

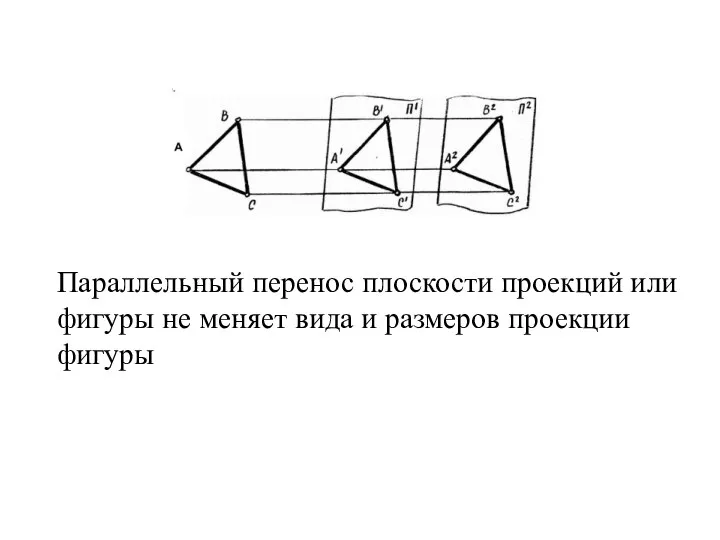
Параллельный перенос плоскости проекций или фигуры не меняет вида и размеров проекции фигуры

ТОЧКА
ТОЧКА

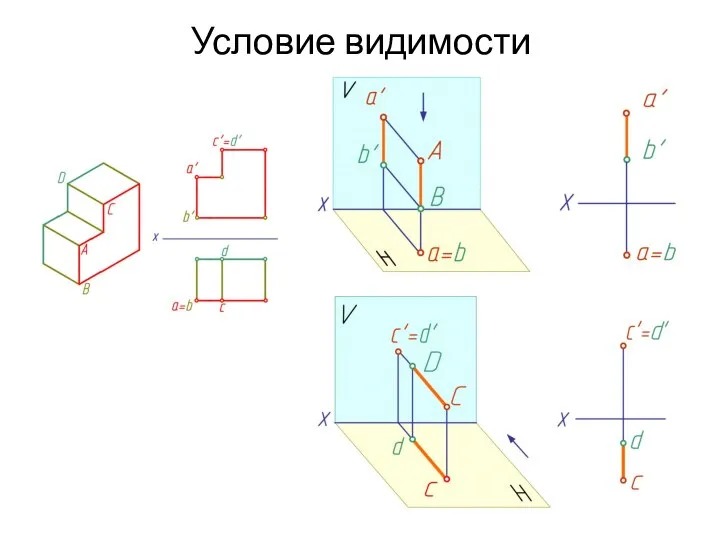
Условие видимости