Не лякайтесь слова "аркус“Адже "аркус" – це кут

Арксинус і його властивості.
Мета:Усвідомлення поняття арксинуса та його властивостей.
Знати: означення арксинуса а, які значення мають a і b у виразі arcsin a = b
Вміти: застосовувати вивчені поняття арксинуса в простих вправах.

І. Актуалізація опорних знань.
Фронтальне опитування.
1. Дати означення зростаючої й спадної функції на проміжку. Як довести, зростає чи спадає дана функція?
2. Як знайти нулі функції?
(Нулі функції знаходимо з умови f(x) =0).
3. Як знайти проміжки знакосталості функції?
а) Проміжки, де функція набуває додатних значень, дістаємо з умови f(x)>0.
б) Проміжки, де функція y= f(x) набуває від'ємних значень, дістаємо з умови f(x)<0.
4. Дати означення парної і непарної функції. Як розміщені їх графіки?
5. Дати означення періодичної функції з періодом Т ≠ 0. Який найменший додатній період функцій синуса, косинуса, тангенса і котангенса?
Чи може періодична функція зростати на всій числовій прямій? Які функції є періодичними?
6. Дати означення оберненої функції і її властивості.
а) Яка необхідна і достатня умова існування оберненої функції?

Необхідна умова існування оборотної функції така: вона має набувати кожного свого значення лише для одного значення аргументу.
Достатня умова існування оберненої функції для даної функції є її монотонність, тобто зростання або спадання на всій області визначення.
б) Алгоритм знаходження формули для оберненої функції.
в) Цікаво, чи має функція у = х2 обернену функцію на R? Яка умова повинна виконуватись? (Щоб була однозначна).
7. Сформулювати теорему про корінь рівняння, функція якого зростає чи спадає на проміжку І.
Відповідь: Теорема про корінь рівняння, функція якого зростає або спадає на проміжку І формулюється так:
Якщо функція f(x) зростає (або спадає) на проміжку І, а число а – будь-яке із значень, яких набуває функція f(x) на цьому проміжку, тоді рівняння f(x) = а має єдиний корінь на проміжку І.

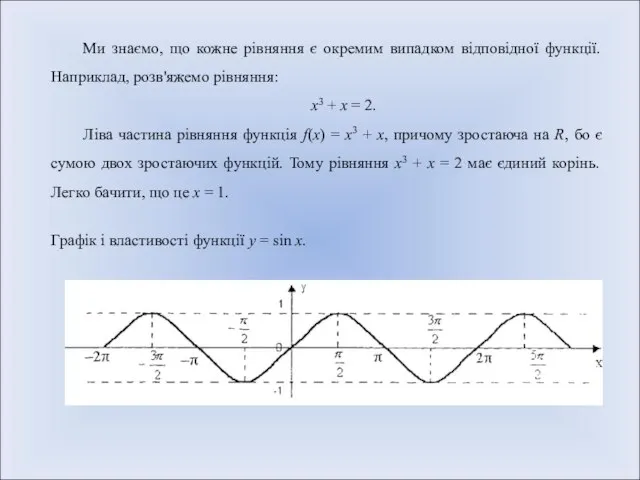
Ми знаємо, що кожне рівняння є окремим випадком відповідної функції. Наприклад, розв'яжемо рівняння:
х3 + х = 2.
Ліва частина рівняння функція f(x) = х3 + х, причому зростаюча на R, бо є сумою двох зростаючих функцій. Тому рівняння х3 + х = 2 має єдиний корінь. Легко бачити, що це х = 1.
Графік і властивості функції у = sin х.

.
.
D(f) = R;
E(f) = [-l;l];
sin (-х) = -sin х;
sin (х + 2πn) = sin х;
sin х = 0 при х = πn, n ∈ z
Зростає на
Спадає на
sin x > 0 при х ∈ (2πn, π + 2πn), n ∈ z
sin х < 0 при х ∈ (-π+2πn, 2πn), n ∈ z
sin х = 1 при
sin х = -1 при

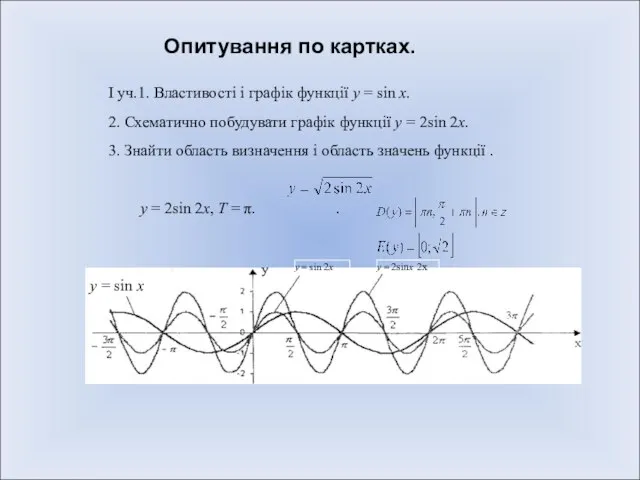
Опитування по картках.
І уч.1. Властивості і графік функції у = sin х.
2. Схематично побудувати графік функції у = 2sin 2х.
3. Знайти область визначення і область значень функції .
у = 2sin 2х, Т = π. .
у = sin x

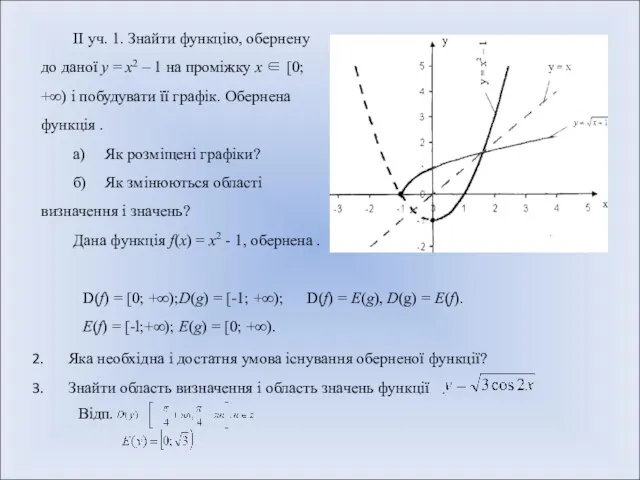
ІІ уч. 1. Знайти функцію, обернену до даної у = х2 – 1 на проміжку х ∈ [0; +∞) і побудувати її графік. Обернена функція .
а) Як розміщені графіки?
б) Як змінюються області визначення і значень?
Дана функція f(x) = х2 - 1, обернена .
D(f) = [0; +∞); D(g) = [-1; +∞); D(f) = E(g), D(g) = E(f).
E(f) = [-l;+∞); E(g) = [0; +∞).
Яка необхідна і достатня умова існування оберненої функції?
Знайти область визначення і область значень функції
Відп.
;

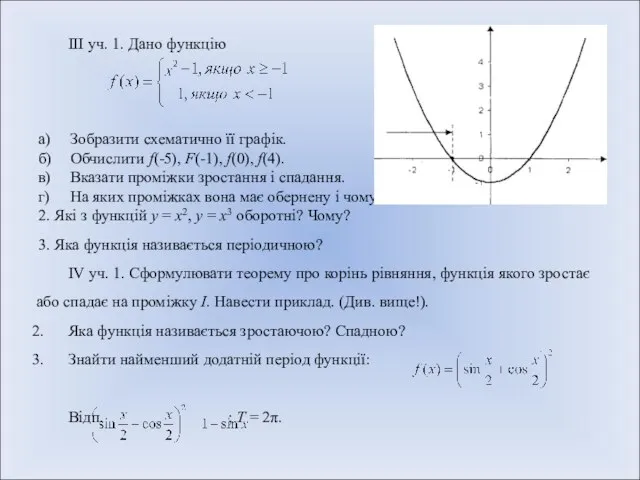
III уч. 1. Дано функцію
а) Зобразити схематично її графік.
б) Обчислити f(-5), F(-1), f(0), f(4).
в) Вказати проміжки зростання і спадання.
г) На яких проміжках вона має обернену і чому?
2. Які з функцій у = х2, у = х3 оборотні? Чому?
3. Яка функція називається періодичною?
IV уч. 1. Сформулювати теорему про корінь рівняння, функція якого зростає або спадає на проміжку І. Навести приклад. (Див. вище!).
Яка функція називається зростаючою? Спадною?
Знайти найменший додатній період функції:
Відп. ; Т = 2π.

II. Мотивація навчання.
Ми з вами навчилися розв'язувати лінійні рівняння, квадратні рівняння, біквадратні рівняння. Щоб розв'язати, наприклад, квадратне рівняння, треба знати формулу його коренів.
Ми знаємо, що кожне рівняння є окремим випадком відповідної функції. Наприклад, ах2 + bх + с = 0, де а ≠ 0 – загальний вид квадратного рівняння, а у = ах2 + bх + с, де а ≠ 0 – квадратична функція.
Ми з вами познайомилися з тригонометричними функціями: у = sin х,
у=cosх, у = tg х, у = ctg х, а отже повинні навчитися розв'язувати прості тригонометричні рівняння sin х = a, cos х = a, tg х = а, ctg х = а.
Нехай дано рівняння sin х = а, де .

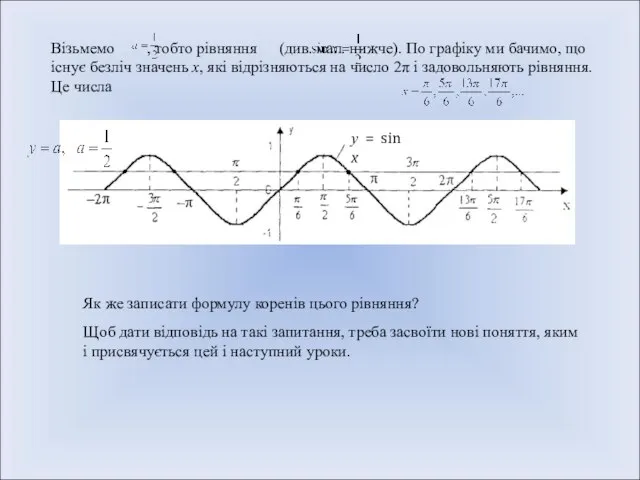
Візьмемо , тобто рівняння (див. мал. нижче). По графіку ми бачимо, що існує безліч значень х, які відрізняються на число 2π і задовольняють рівняння. Це числа
у = sin x
Як же записати формулу коренів цього рівняння?
Щоб дати відповідь на такі запитання, треба засвоїти нові поняття, яким і присвячується цей і наступний уроки.

III. Сприймання й усвідомлення поняття арксинуса.
І так, тема сьогоднішнього уроку:
Арксинус і його властивості.
Застосуємо раніше вивчену теорему про єдиність кореня рівняння f(x) = а,
функція якого зростає (або спадає) на проміжку І, до рівняння sin х = а.

Бачимо з графіка, що функція у = sin х на проміжку монотонно зростає і набуває на ньому всіх своїх значень від -1 до 1. А тому згідно з теоремою про корінь рівняння для будь-якого числа а, такого що в проміжку існує єдиний корінь b рівняння sin х = а. Цей корінь – число b (кут або дуга) і назвали арксинусом числа а і позначили arcsin а. Отже, arcsinа = b, де
або
Отже, (arcsinа) арксинусом числа а називається кут (число), заключений у проміжку , синус якого дорівнює a.
Тобто
, бо
Отже, ще раз підкреслимо: з означення арксинуса випливає, що

IV. Розв'язування вправ на закріплення.
1.Розглянемо
– це такий кут з проміжку
що його синус дорівнює
Відомо, що це
звідси
бо
і
2. Обчислити:
a)
, бо
і
б)
, бо
і
в)
, бо
і
г) arsin 1,5 – не має змісту, бо
д)
е)
є)
ж)
– не має змісту, бо

Запам'ятати:
arcsin 0 = 0; 2) 3) 4)
5) 6)
.
Властивості арксинуса a:
; 3) arcsin(- a) = -arcsin a,
; 4) Значення .

Самостійна робота.
Обчислити:
1) ; 1) ;
2) arcsin 2,5 – не має змісту; 2) ;
arcsin 0 = 0, 3) arcsin 1,5 – не має змісту;
; 4) ;
5) cos(arcsin l) = 0; 5) tg(arcsin 0) = 0;
6) ; 6) ,
7) ; 7) .
Перейдемо тепер від рівняння sinх=а до функції. Кожне рівняння є окремий випадок відповідної функції. Отже, і рівняння sinх = а, де у = sin х –функція, а а – окреме число, причому обмежене |а| < 1 , бо .
Чи має вона до себе обернену?

З графіка видно, що функція у = sin х на відрізку монотонно зростає від -1 до 1 і приймає всі значення, що належать цьому проміжку, причому кожне із значень по одному разу, тобто множина значень і взаємно однозначно відображаються одна на одну.
А якщо функція у = sin х на зростає і неперервна, то вона має обернену функцію, зростаючу і неперервну. Цю функцію назвали арксинусом і позначили у = arcsin х.
Згідно означення оберненої функції, її область визначення є відрізок [-1; 1], а множиною значень відрізок .
Графік функції у = arcsin x, де x ∈ [-1; 1] симетричний графіку у = sin х, де x ∈ відносно бісектриси у = х.