семинар 1 дÐя СОЗ

Учебные вопросы
Принципы получения радиолокационной информации.
Радиолокационные сигналы и их характеристики.
Оптимальное обнаружение сигналов и измерение их параметров.
Расчет характеристик радиолокационного обзора.

Вопрос 1
Принципы получения радиолокационной информации

Основные определения радиолокации

Этапы получения радиолокационной информации

Основные положения:
Информация получается за счет возмущения среды целью, в частности, за счет эффекта переизлучения целью радиоволн.
Для получения необходимой информации учитываются и используются реальные закономерности распространения радиоволн в пространстве.
Выделение слабых сигналов, приходящих от цели, и разрешение целей обеспечивается за счет различий сигналов и помех, а также сигналов от разных целей между собой.
Информация о целях получается параллельно или последовательно во времени и выдается в виде информационных потоков.
Принципы получения радиолокационной информации

Эффективная поверхность рассеяния целей

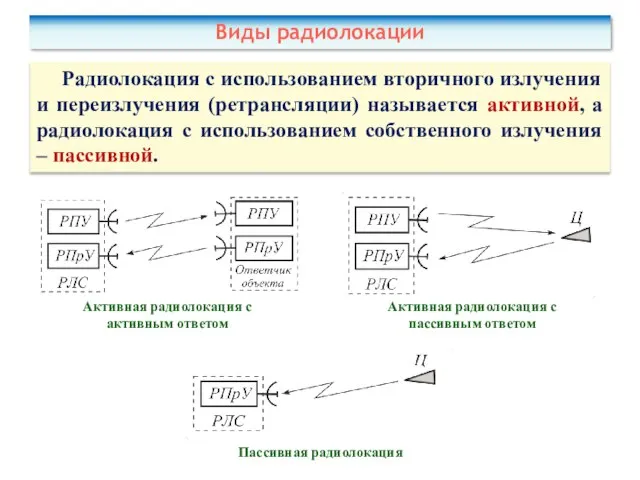
Радиолокация с использованием вторичного излучения и переизлучения (ретрансляции) называется активной, а радиолокация с использованием собственного излучения – пассивной.
Виды радиолокации
Пассивная радиолокация
Активная радиолокация с активным ответом
Активная радиолокация с пассивным ответом

Время запаздывания отраженного сигнала относительно зондирующего для совмещенной РЛС определяется соотношением: tз = 2r/с.
Принцип измерения дальности до цели
Тогда дальность до цели равна:

Измерение радиальной скорости Vr цели основано на эффекте Доплера:
Отраженный от движущейся цели сигнал оказывается смещенным по частоте относительно зондирующего сигнала на величину частоты Доплера FД, пропорциональную радиальной скорости цели:
Принцип измерения радиальной скорости цели
Тогда радиальная скорость цели равна:

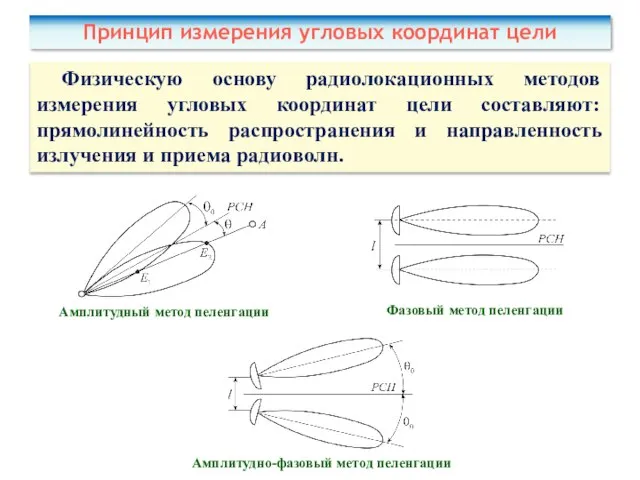
Физическую основу радиолокационных методов измерения угловых координат цели составляют: прямолинейность распространения и направленность излучения и приема радиоволн.
Принцип измерения угловых координат цели
Амплитудно-фазовый метод пеленгации
Фазовый метод пеленгации
Амплитудный метод пеленгации

Несущая частота f0 (длина волны λв ).
Параметры зондирующего сигнала (ширина спектра ∆f0, длительность τс, период повторения Tп).
Характеристики радиопередающего устройства (РПУ) РЛС:
излучаемая (импульсная) мощность Pи;
коэффициент усиления Gп;
скважность Q (для импульсных РЛС);
Характеристики радиоприемного устройства (РПрУ) РЛС:
чувствительность приемного устройства Pпр;
коэффициент усиления Gпр;
шумовая температура РПрУ T0;
коэффициент шума РПрУ kш ;
Характеристики антенного устройства РЛС.
Технические характеристики РЛС

Под тактическими характеристиками понимают характеристики, описывающие возможности практического использования РЛС.
Основными тактическими характеристиками любой РЛС являются:
• зона действия;
• максимальная дальность действия;
• разрешающая способность;
• точность измерения координат цели;
• пропускная способность;
• помехозащищенность;
• надежность.
Тактические характеристики РЛС

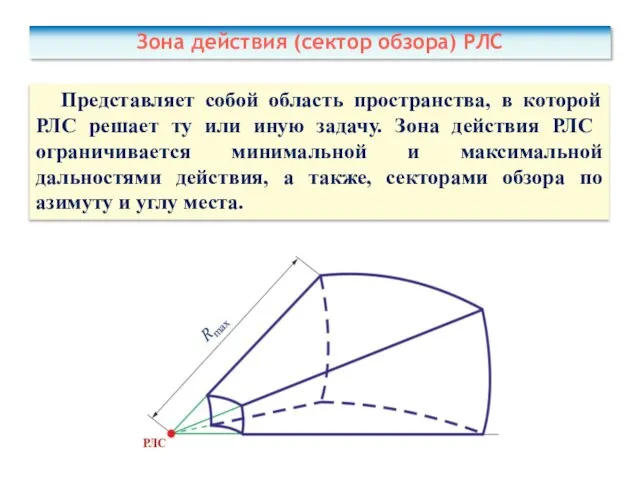
Представляет собой область пространства, в которой РЛС решает ту или иную задачу. Зона действия РЛС ограничивается минимальной и максимальной дальностями действия, а также, секторами обзора по азимуту и углу места.
Зона действия (сектор обзора) РЛС

Зависит не только от параметров РЛС, но и от ЭПР наблюдаемых целей:
Максимальная дальность действия РЛС
kБ – коэффициент Больцмана, определяющий связь между темпе-
ратурой и энергией;
q2 – отношение сигнал/шум на входе приемного устройства РЛС. Является безразмерной величиной, равной отношению мощности полезного сигнала к мощности шума на входе приемного устройства РЛС.

Способность РЛС осуществлять раздельное радиолокационное наблюдение целей.
Разрешающая способность РЛС
Определяется максимальным числом одновременно сопровождаемых целей (элементов для сложных целей), по которым на заданных рубежах были выполнены критерии обнаружения, захвата и сопровождения, и выдана вся необходимая информация.
Пропускная способность РЛС

Способность РЛС сохранять свои тактико-технические характеристики в заданных допусках при определенных условиях эксплуатации.
Оценивается надежность обычно вероятностью безотказной работы РЛС в течение установленного промежутка времени или средним временем исправной работы РЛС (частотой отказов).
Надежность РЛС
Определяется абсолютным значением система-тической ошибки и среднеквадратическим значением случайной ошибки.
Точность измерения координат целей

При решении задач получения и обработки радиолокационной информации используются следующие системы координат:
1. Географическая система координат (ГСК).
2. Геоцентрическая система координат (ГЦСК).
3. Местные (топоцентрические) системы координат (МСК).
4. Антенные системы координат (АСК).

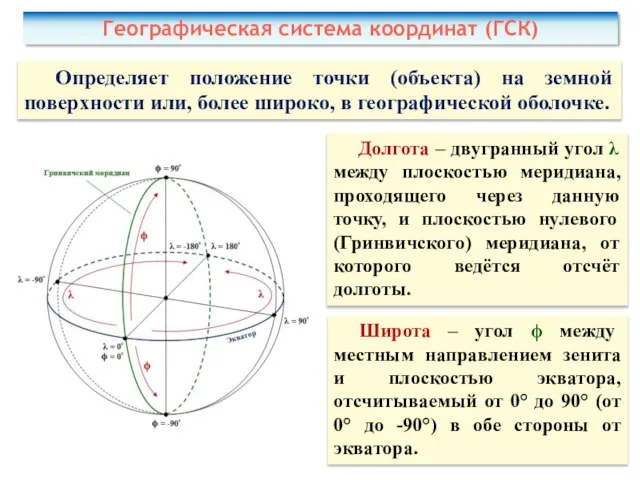
Географическая система координат (ГСК)
Определяет положение точки (объекта) на земной поверхности или, более широко, в географической оболочке.
Широта – угол ϕ между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° (от 0° до -90°) в обе стороны от экватора.
Долгота – двугранный угол λ между плоскостью меридиана, проходящего через данную точку, и плоскостью нулевого (Гринвичского) меридиана, от которого ведётся отсчёт долготы.

Геоцентрическая система координат (ГЦСК)
В ГЦСК которой координаты объекта задаются вектором (xg, yg, zg) прямоугольной системы координат c центром в центре Земли.
Ось Z проходит через северный полюс, ось X проходит через точку пересечения линии экватора и гринвичского меридиана, а ось Y дополняет систему до правой системы координат.

Местные системы координат (МСК)
Местными (топоцентрическими) системами координат (МСК) называют такие системы координат, начало которых находится в точке наблюдения (в радиолокации – точки стояния РЛС).
Различают:
• местную прямоугольную систему координат;
• местную сферическую систему координат.

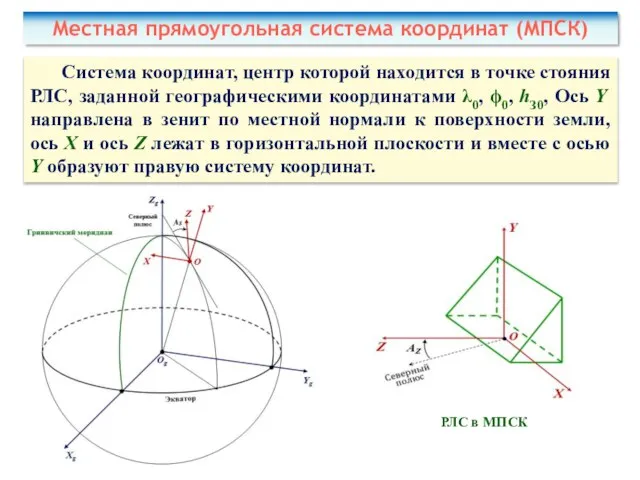
Местная прямоугольная система координат (МПСК)
Система координат, центр которой находится в точке стояния РЛС, заданной географическими координатами λ0, ϕ0, hЗ0, Ось Y направлена в зенит по местной нормали к поверхности земли, ось X и ось Z лежат в горизонтальной плоскости и вместе с осью Y образуют правую систему координат.
РЛС в МПСК

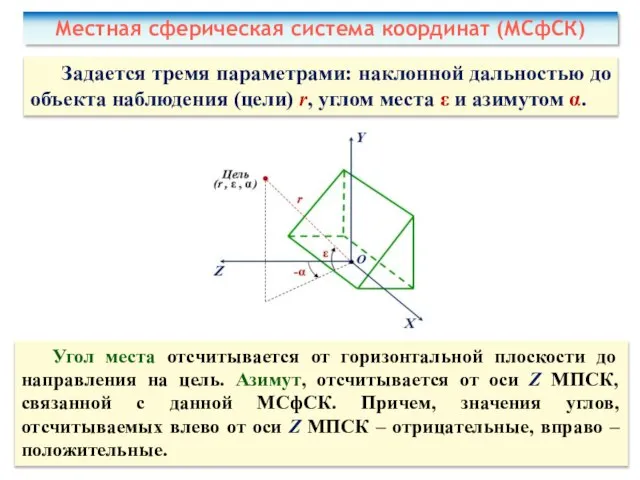
Местная сферическая система координат (МСфСК)
Задается тремя параметрами: наклонной дальностью до объекта наблюдения (цели) r, углом места ε и азимутом α.
Угол места отсчитывается от горизонтальной плоскости до направления на цель. Азимут, отсчитывается от оси Z МПСК, связанной с данной МСфСК. Причем, значения углов, отсчитываемых влево от оси Z МПСК – отрицательные, вправо – положительные.

Антенные системы координат (АСК)
Антенными системами координат (АСК) называют такие системы координат, начало отсчета, которых совмещено с центром антенной системы РЛС.
Различают:
• антенную прямоугольную систему координат;
• антенную биконическую систему координат;
• антенную сферическую систему координат.

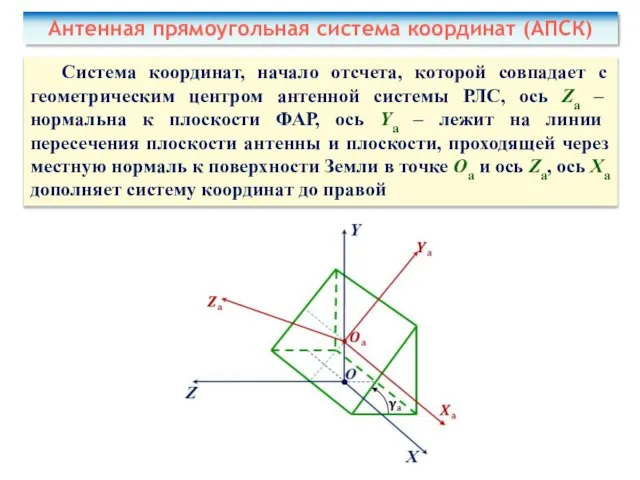
Антенная прямоугольная система координат (АПСК)
Система координат, начало отсчета, которой совпадает с геометрическим центром антенной системы РЛС, ось Zа – нормальна к плоскости ФАР, ось Yа – лежит на линии пересечения плоскости антенны и плоскости, проходящей через местную нормаль к поверхности Земли в точке Оа и ось Zа, ось Xа дополняет систему координат до правой

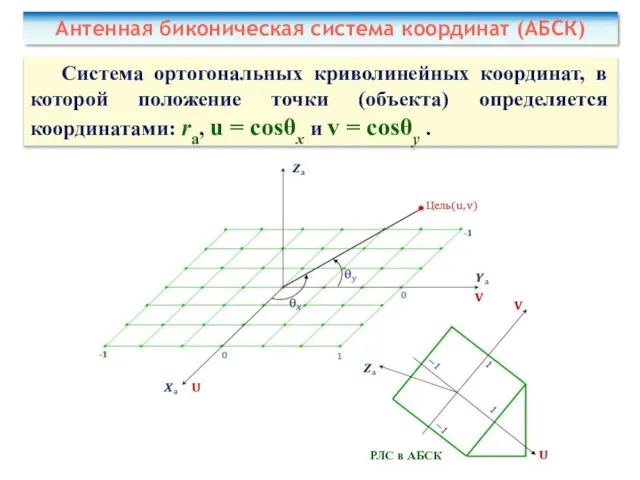
Антенная биконическая система координат (АБСК)
Система ортогональных криволинейных координат, в которой положение точки (объекта) определяется координатами: rа, u = cosθx и v = cosθy .
РЛС в АБСК

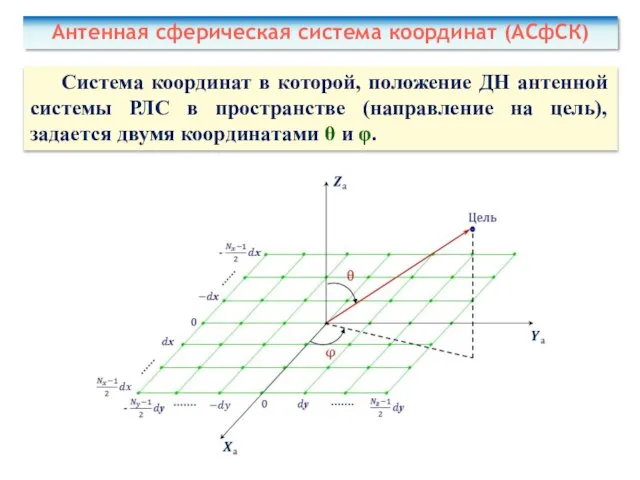
Антенная сферическая система координат (АСфСК)
Система координат в которой, положение ДН антенной системы РЛС в пространстве (направление на цель), задается двумя координатами θ и φ.

Вопрос 2
Радиолокационные сигналы и их характеристики

Под радиолокационным (зондирующим) сигналом в радиолокации понимают электромагнитную волну, излучаемую антенным устройством РЛС.
В зависимости от назначения РЛС зондирующий сигнал должен позволять реализовывать:
• энергию излучения, достаточную для обнаружения целей и оценки их параметров;
• требуемое разрешение целей;
• достаточное подавление помех (нежелательных отраженных сигналов).
Радиолокационные сигналы

a(t) – функция, выражающая амплитудную модуляцию сигнала;
φ(t) – функция, выражающая фазовую модуляцию сигнала;
ω0 = 2πf0 – круговая несущая частота сигнала;
f0 – несущая частота сигнала.
Представление РЛ сигнала во временной области

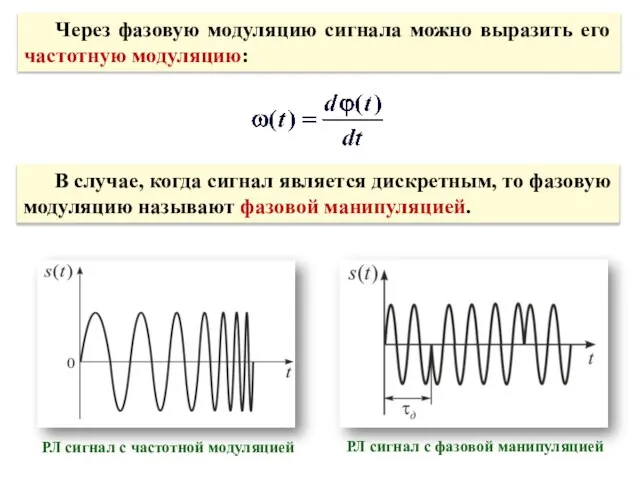
Через фазовую модуляцию сигнала можно выразить его частотную модуляцию:
В случае, когда сигнал является дискретным, то фазовую модуляцию называют фазовой манипуляцией.
РЛ сигнал с частотной модуляцией
РЛ сигнал с фазовой манипуляцией

Представление РЛ сигнала в частотной области

Автокорреляционная функция (АКФ) сигнала

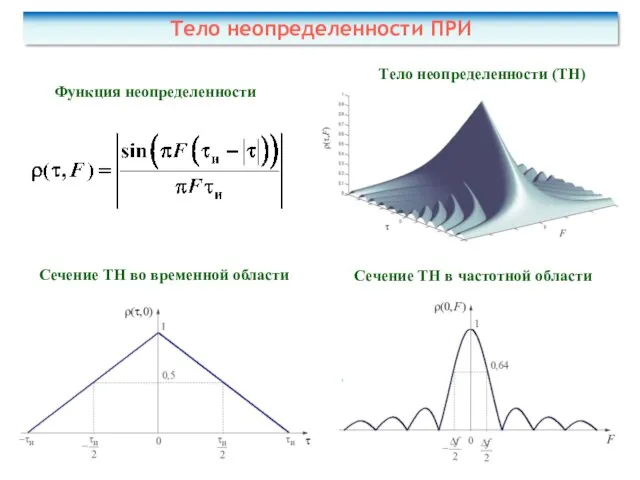
Функция неопределенности сигнала
Функцией неопределенности (рассогласования) сиг-нала называют его нормированную двумерную АКФ:
τ и F – рассогласования сигнала по времени запаздывания и доплеровской частоте.

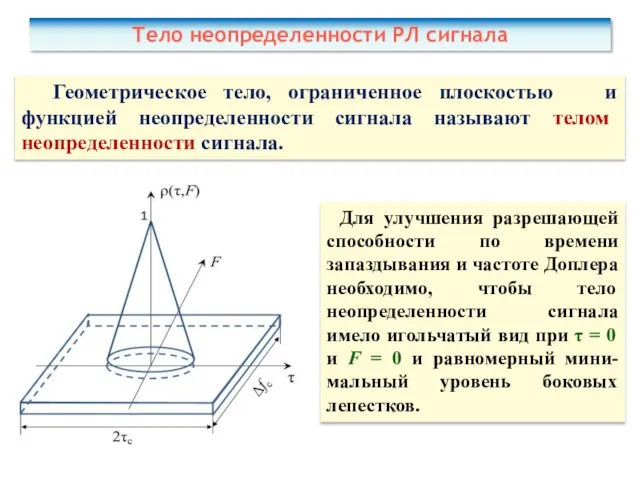
Геометрическое тело, ограниченное плоскостью и функцией неопределенности сигнала называют телом неопределенности сигнала.
Тело неопределенности РЛ сигнала
Для улучшения разрешающей способности по времени запаздывания и частоте Доплера необходимо, чтобы тело неопределенности сигнала имело игольчатый вид при τ = 0 и F = 0 и равномерный мини-мальный уровень боковых лепестков.

Мощность сигнала P(t)
Энергия сигнала Е
Длительность сигнала τс , определяющая интервал времени, в течение которого сигнал существует
Ширина спектра сигнала Δfс – полоса частот, в пределах которой сосредоточена основная энергия сигнала
База сигнала – произведение длительности сигнала на ширину его спектра: B = τс∙Δfс
Основные параметры радиолокационных сигналов

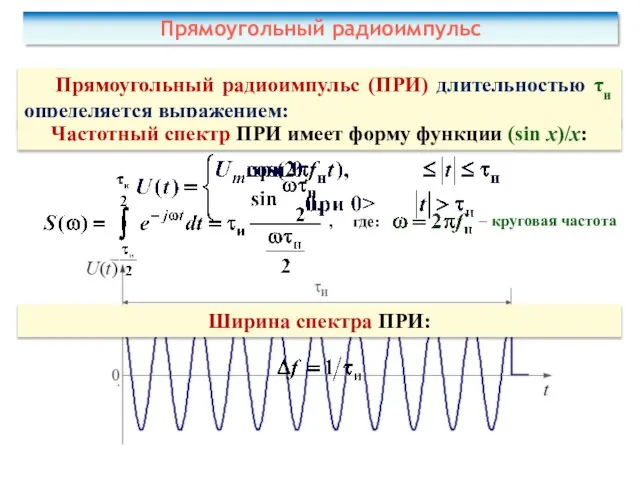
Прямоугольный радиоимпульс

Тело неопределенности ПРИ
Функция неопределенности
Тело неопределенности (ТН)
Сечение ТН во временной области
Сечение ТН в частотной области

Преимущества: простота генерации и обработки.
Прямоугольный радиоимпульс
Недостатки: невозможность обеспечить одновременно хорошее разрешение по дальности (для чего требуется импульс малой длительности) и большую энергию сигнала (для чего требуется импульс большой длительности).

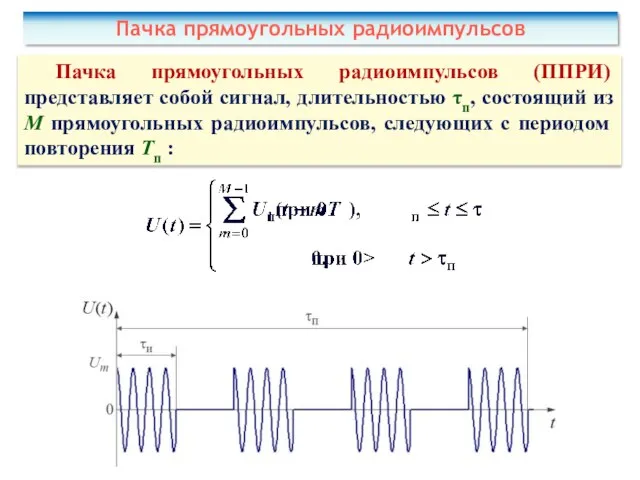
Пачка прямоугольных радиоимпульсов
Пачка прямоугольных радиоимпульсов (ППРИ) представляет собой сигнал, длительностью τп, состоящий из M прямоугольных радиоимпульсов, следующих с периодом повторения Tп :

Пачка прямоугольных радиоимпульсов
Частотный спектр ППРИ:
Ширина спектра ППРИ:
Функция неопределенности ППРИ:
– функция неопределенности одного ПРИ, входящего в ППРИ

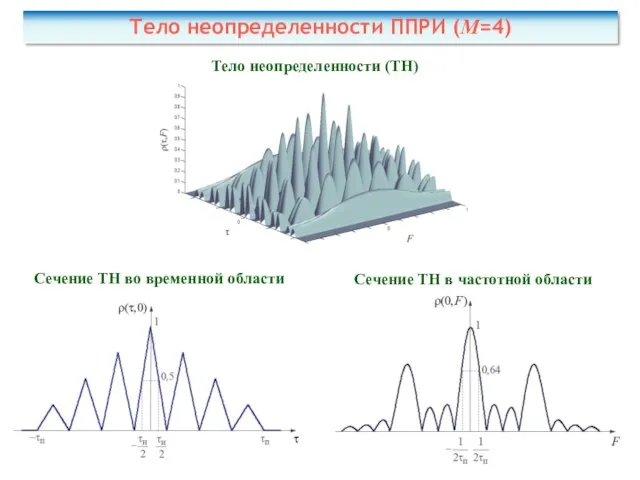
Тело неопределенности ППРИ (M=4)
Тело неопределенности (ТН)
Сечение ТН во временной области
Сечение ТН в частотной области

Преимущества: пачечные сигналы обеспечивают существенно более высокую разрешающую способность по частоте (радиальной скорости).
Пачка прямоугольных радиоимпульсов
Недостатки: в силу периодического характера проявляется неоднозначность измерений времени запаздывания (дальности) и частоты (радиальной скорости).

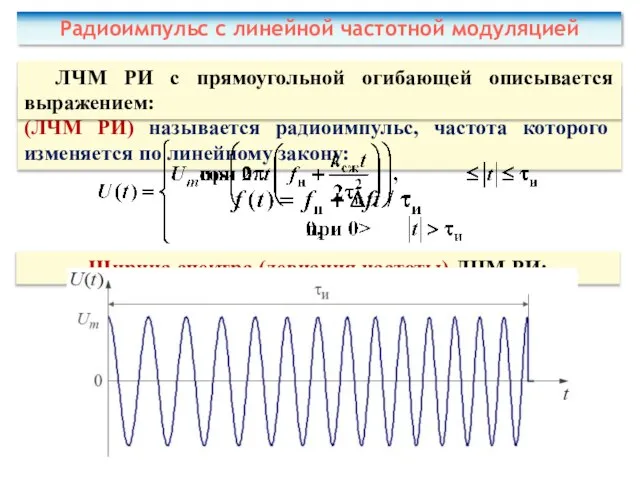
Радиоимпульс с линейной частотной модуляцией

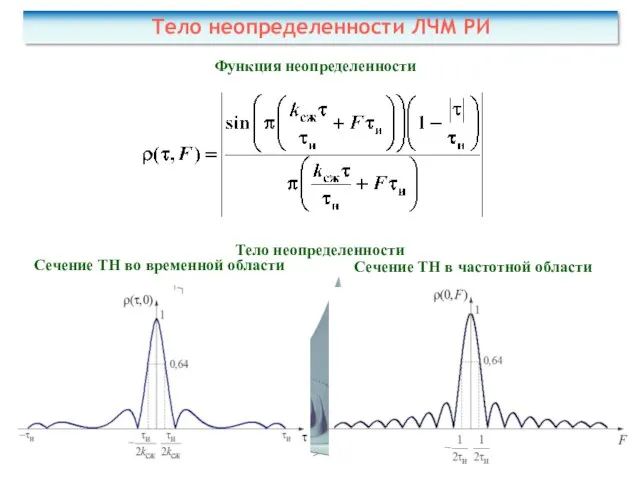
Тело неопределенности ЛЧМ РИ
Функция неопределенности

Преимущества: в результате корреляционной обработки длительность ЛЧМ РИ уменьшается, что позволяет повысить точность измерений и разрешать близко расположенные объекты.
ЛЧМ РИ
Недостатки: сложность формирования сигналов большой длительности.

Радиоимпульс с фазокодовой манипуляцией
Радиоимпульс с фазокодовой манипуляцией (ФКМ РИ) – это совокупность Nд сомкнутых прямоугольных радиоимпульсов (дискрет) одинаковой длительности и частоты при ограниченном числе р различающихся возможных значений начальной фазы сигнала.
Ширина спектра ФКМ РИ:
где τд – длительность дискрета
При р = 2, фазовая манипуляция называется бинарной фазовой манипуляцией. Фаза такого сигнала изменяется, попеременно принимая значения 00 или 1800, в соответствии с чередованием элементов бинарного кода 1 и -1.

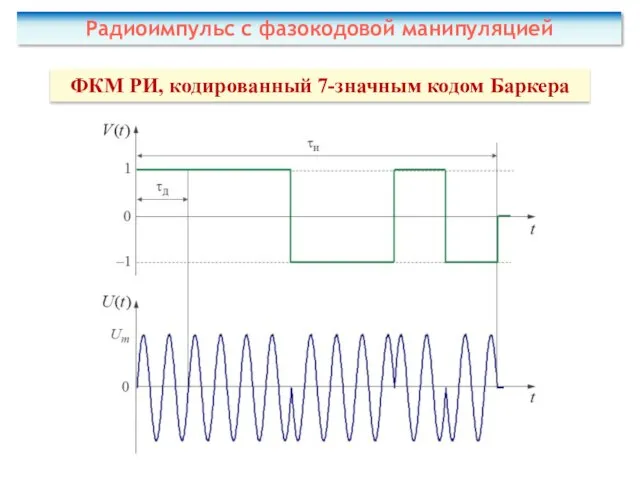
ФКМ РИ, кодированный 7-значным кодом Баркера
Радиоимпульс с фазокодовой манипуляцией

Радиоимпульс с фазокодовой манипуляцией
Огибающая одного дискрета кода:
Временное представление сигнала:
где qk – код фазовой манипуляции (например: qk = [111-1-11-1]Т)
Огибающая кода:

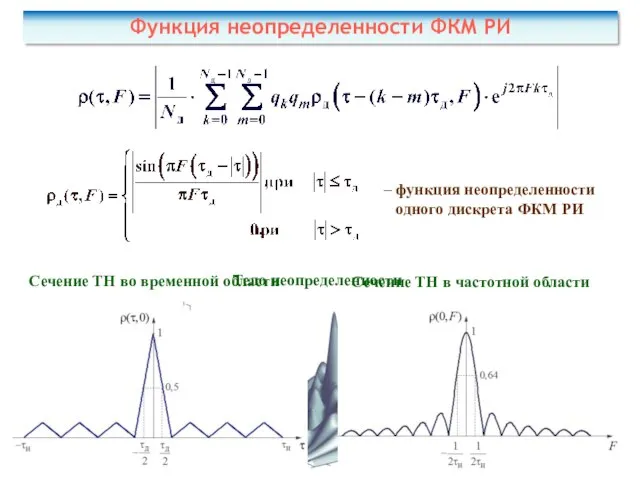
Функция неопределенности ФКМ РИ
– функция неопределенности
одного дискрета ФКМ РИ

ФКМ РИ, кодированный 31-значной М-последовательностью
ФКМ РИ, кодированные М-последовательностями

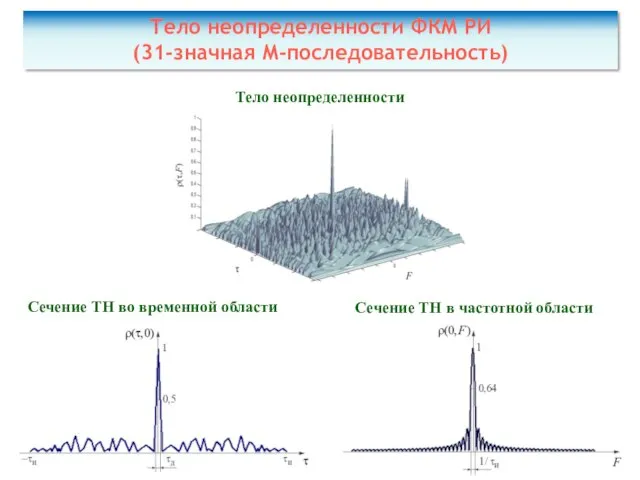
Тело неопределенности ФКМ РИ
(31-значная М-последовательность)
Тело неопределенности
Сечение ТН во временной области
Сечение ТН в частотной области

Преимущества: энергоемкость и высокая разрешающая способность одновременно по времени и по частоте (дальности и скорости).
ФКМ РИ
Недостатки: сложность формирования сигналов большой длительности.

Вопрос 3
Оптимальное обнаружение сигналов и измерение их параметров

В результате процесса обнаружения должно быть выдано решение о наличии или отсутствии цели в произвольном разрешаемом объеме зоны действия РЛС.
Решение может быть принято при двух взаимно исключающих условиях:
• условие А1 – «цель есть»,
• условие А0 – «цели нет»,
которые при выработке решения неизвестны.
За счет помех и флюктуаций полезного сигнала каждому условию могут соответствовать два вида решений:
• решение А1* – «цель есть»,
• решение А0* – «цели нет».
Третьего решения – «не знаю» – после завершения процесса обнаружения быть не должно.

При обнаружении возможны четыре ситуации совмещения случайных событий «решения» и «условия»:
1) ситуация А1*А1 – «правильное обнаружение»;
2) ситуация А0*А1 – «пропуск цели»;
3) ситуация А1*А0 – «ложная тревога»;
4) ситуация А0*А0 – «правильное необнаружение».
Перечисленным ситуациям соответствуют четыре вероятности совмещения событий, сумма которых равна единице:

Если каждому ошибочному решению поставить в соответствие некоторую плату – стоимость ошибки rik (i = = 0, 1; k = 0, 1), и для безошибочных решений условиться считать эту стоимость равной нулю r11 = r00 = 0, то систему обнаружения можно характеризовать средней стоимостью (математическим ожиданием стоимости) ошибочных решений:
Лучшей из сравниваемых систем обработки можно тогда считать систему, удовлетворяющую критерию минимума этой стоимости, иначе – критерию минимума среднего риска.

Критерий минимума среднего риска основан на введении неотрицательных стоимостей ущерба (штрафов) rik за неправильные решения (i ≠ k). За правильные решения штраф задается отрицательным (премия) или нулевым.

Преобразуем выражение для среднего риска:
где l0 – весовой множитель, равный:
Критерий минимума среднего риска сводится, таким образом, к весовому критерию:

Условные вероятности правильного обнаружения и ложной тревоги определяются выбором решающей функции и плотностями вероятностей реализаций сигнала и помехи («сп») и только одной помехи («п»):
Объем Vy многомерного пространства y разбит на элементарные объемы dVy . Произведения условных плотностей вероятности на эти объемы определяют элементарные вероятности попадания в них реализаций у при условиях «сп» или «п».

Оптимальное решающее правило
Отношение условных плотностей вероятностей как функций одной и той же принятой реализации у при условиях наличия сигнала и помехи и только помехи называется отношением правдоподобия:
Отношение правдоподобия влияет на выбор оптимальной решающей функции. Большие значения l(у) характеризуют правдоподобность гипотезы о наличии сигнала.

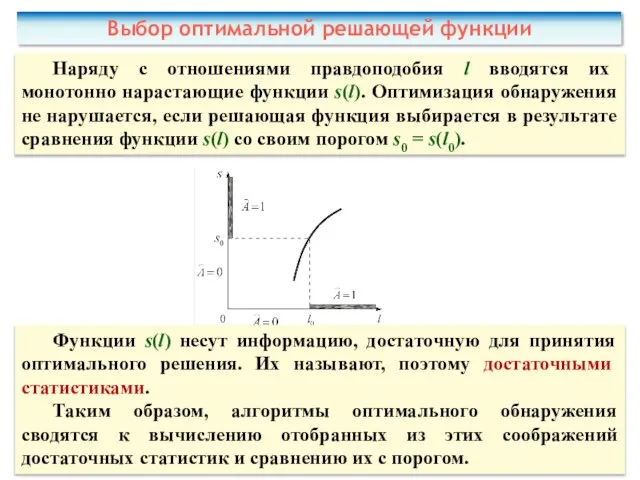
Наряду с отношениями правдоподобия l вводятся их монотонно нарастающие функции s(l). Оптимизация обнаружения не нарушается, если решающая функция выбирается в результате сравнения функции s(l) со своим порогом s0 = s(l0).
Функции s(l) несут информацию, достаточную для принятия оптимального решения. Их называют, поэтому достаточными статистиками.
Таким образом, алгоритмы оптимального обнаружения сводятся к вычислению отобранных из этих соображений достаточных статистик и сравнению их с порогом.
Выбор оптимальной решающей функции

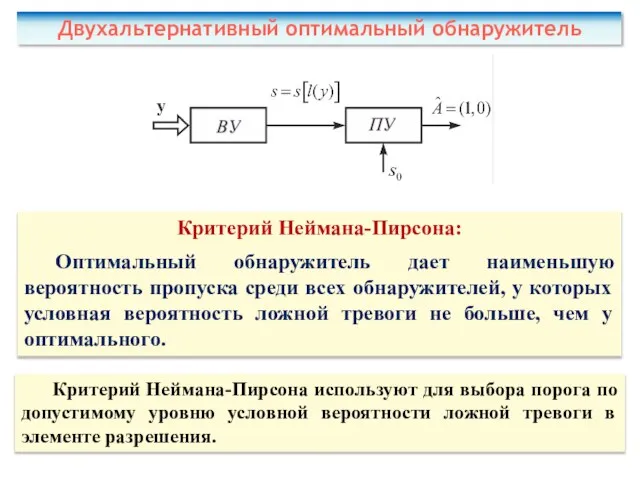
Двухальтернативный оптимальный обнаружитель
Критерий Неймана-Пирсона:
Оптимальный обнаружитель дает наименьшую вероятность пропуска среди всех обнаружителей, у которых условная вероятность ложной тревоги не больше, чем у оптимального.
Критерий Неймана-Пирсона используют для выбора порога по допустимому уровню условной вероятности ложной тревоги в элементе разрешения.

Ошибки измерения параметров цели
Если в результате проведенного измерения должна быть дана оценка α* каждого измеряемого параметра α, то показателем качества измерения является статистически усредненная величина ошибки ε = α*- α измерения параметра. Чем меньше величина ошибки, тем выше качество измерения.
Ошибки измерений делятся на:
• грубые промахи;
• систематические ошибки;
• случайные ошибки.
Если приняты меры для исключения систематических ошибок и грубых промахов, ошибки измерений сводятся к случайным.

Для произвольного закона распределения случайных ошибок p(ε) среднеквадратичная ошибка измерения определяется из соотношения:
Качественными показателями измерения одномерной случайной величины являются:
• среднеквадратичная ошибка;
• вероятная (срединная) ошибка;
• максимальная ошибка;
• математическое ожидание;
• дисперсия и др.
Случайные ошибки обусловлены действием помех на входе приемника РЛС, флюктуациями сигнала, а иногда случайным поведением самой системы измерений.

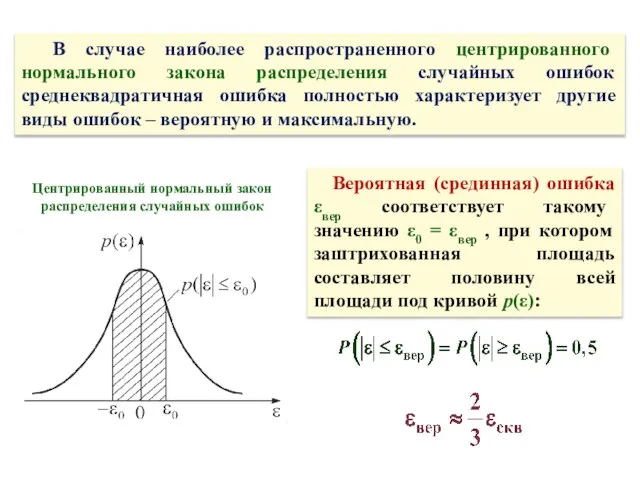
В случае наиболее распространенного центрированного нормального закона распределения случайных ошибок среднеквадратичная ошибка полностью характеризует другие виды ошибок – вероятную и максимальную.
Вероятная (срединная) ошибка εвер соответствует такому значению ε0 = εвер , при котором заштрихованная площадь составляет половину всей площади под кривой p(ε):
Центрированный нормальный закон распределения случайных ошибок

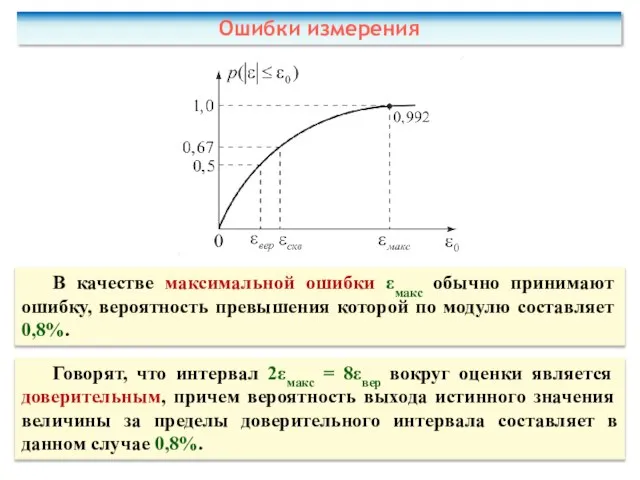
В качестве максимальной ошибки εмакс обычно принимают ошибку, вероятность превышения которой по модулю составляет 0,8%.
Говорят, что интервал 2εмакс = 8εвер вокруг оценки является доверительным, причем вероятность выхода истинного значения величины за пределы доверительного интервала составляет в данном случае 0,8%.
Ошибки измерения

Математическое ожидание ошибки M{ε} отлично от нуля, когда действует источник систематической ошибки. Оценку α* в этом случае называют смещенной.
Дисперсия ошибки определяется выражением:
В случае несмещенной оценки D{ε} совпадает со средним квадратом ошибки:

В качестве обобщенного критерия качества измерения можно ввести средний риск ошибки измерения. Для этого рассмотрим совокупность ситуаций совмещения случайного значения параметра α и случайной оценки α* .
Для каждой из ситуаций введем совместную плотность вероятности p(α*,α) и дифференциальную вероятность совме-щения:
Каждой ситуации совмещения поставим в соответствие некоторую стоимость ошибки r(α*,α) в зависимости от ее важности. Тогда критерием качества оценки α* является средняя стоимость (средний риск) ошибки измерений:

Пусть на вход измерителя поступают колебания у(t) в виде наложения флюктуационной помехи и сигнала:
При решении задачи измерения наряду с непрерывными реализациями входных колебаний у(t) введем соответствующие дискретные многомерные реализации Y с целью более удобного использования соотношений теории вероятностей:
– известная функция времени случайного измеряемого параметра α и случайных неизмеряемых параметров β, имеющих заданную плотность вероятности p(β).
– условный средний риск ошибки измерений.

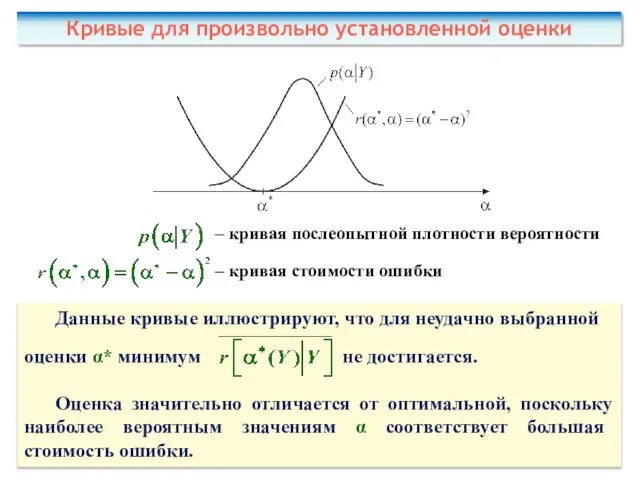
– кривая послеопытной плотности вероятности
– кривая стоимости ошибки
Кривые для произвольно установленной оценки
Данные кривые иллюстрируют, что для неудачно выбранной
оценки α* минимум не достигается.
Оценка значительно отличается от оптимальной, поскольку наиболее вероятным значениям α соответствует большая стоимость ошибки.

Оптимальная по минимуму среднеквадратичной ошибки оценка αопт* представляет собой математическое ожидание измеряемого параметра, соответствующее кривой послеопытной плотности вероятности для принятой реализации Y:
Минимальный средний квадрат возможной ошибки определяется дисперсией распределения послеопытной плотности вероятности для принятой реализации Y:

Плотность вероятности совмещения случайных событий:
Послеопытная плотность вероятности параметра

Аналог формулы полной вероятности
Аналог формулы Байеса

Вопрос 4
Расчет характеристик радиолокационного обзора

Под радиолокационным обзором понимают поэлементное облучение зоны обзора РЛС для выявления имеющихся в зоне целей и измерения их координат и параметров движения.
Обзор по угловым координатам производится перемещением ДН антенны РЛС по такому закону, чтобы за один цикл облучить всю зону. Длительность этого цикла называется периодом обзора Tобз.
Радиолокационный обзор
Периодом облучения Тобл точечной цели называется время, протекающее с момента начала излучения радиоволн в направлении данной цели до конца приема отраженного сигнала от этой цели:

Параллельный обзор одним неподвижным лучом ДН ФАР применяют в РЛС, измеряющих только дальность и, следовательно, не нуждающихся в сканировании луча, например, в самолетных радиовысотомерах и дальномерах.
Методы радиолокационного обзора
Однолучевой обзор со сканированием называют последовательным, так как он требует последовательного облучения всех элементов зоны.

Последовательный обзор, при котором луч ДН передвигается по горизонтальным строкам зоны обзора с периодическим изменением угла места называют построчным.
Построчный радиолокационный обзор

Количество элементов обзора в одной строке зоны обзора можно рассчитать как:
Радиолокационный обзор
Период обзора одной строки зоны обзора РЛС равен произведению количества элементов обзора и периода облучения каждого из них:
Период обзора всей зоны обзора моноимпульсной РЛС (Nс=1) рассчитывается как:

Отработать материал занятия с использованием рекомендуемой литературы.
Подготовиться к следующему занятию.
Быть готовым к контрольному опросу по изученному материалу.
Задание на самостоятельную подготовку

Чепурнов И.А., Серов С.А., Воротнюк Ю.С. Военно-техническая подготовка. Введение в специальность. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2012.
Федоров И.Б. Информационные технологии в радиотехнических системах. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2011.
Леонов А.И., Леонов С.А., Нагулинко Ф.В. Испытания РЛС. Оценка характеристик. – М.: Радио и связь, 1990.
Литература