Теорема Пифагора 8 класс

(ок. 580 – ок. 500 г. до н.э.)
Пифагор Самосский

Открытия пифагорейцев
Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:
теорема о сумме внутренних углов треугольника;
построение правильных многоугольников и деление плоскости на некоторые из них;
геометрические способы решения квадратных уравнений;
деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;
доказательство того, что корень из 2 не является рациональным числом;
создание математической теории музыки, учения об арифметических, геометрических и гармонических пропорциях и многое другое.

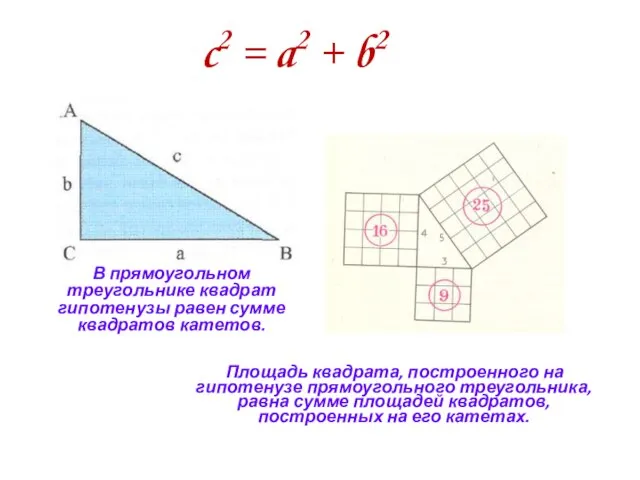
c2 = a2 + b2
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

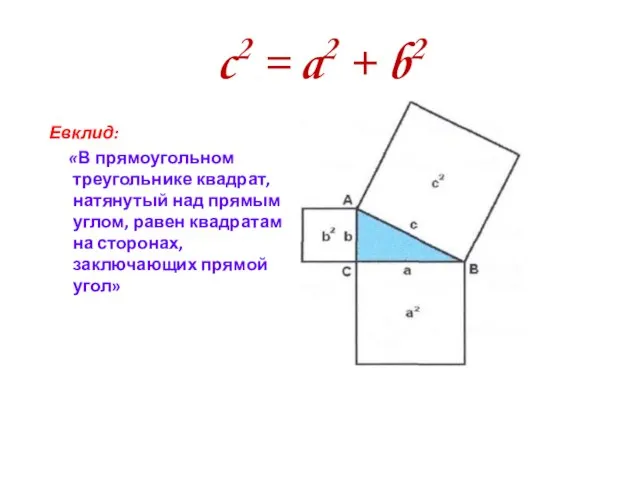
c2 = a2 + b2
Евклид:
«В прямоугольном треугольнике квадрат, натянутый над прямым углом, равен квадратам на сторонах, заключающих прямой угол»

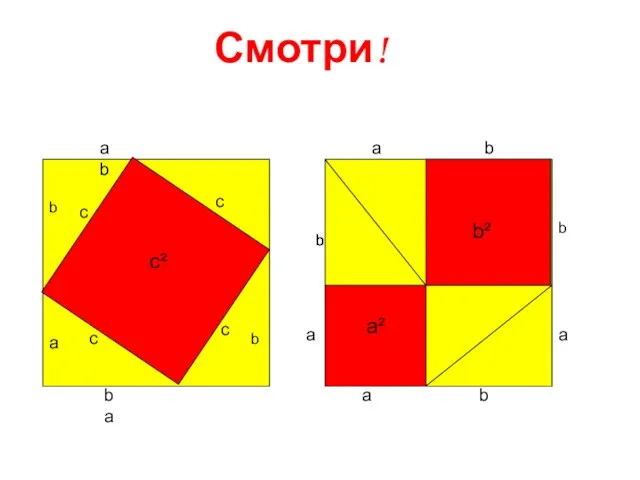
Смотри!
a b
a b
a b
b a
b
b
b
b
b
a
a
a
c
c
c
c
c
a²
b²
c²

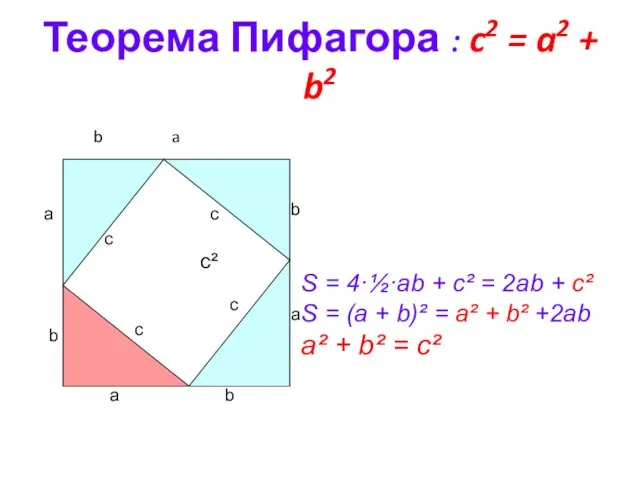
Теорема Пифагора : c2 = a2 + b2
b a
b b
b
a
a
a
c
c
c
c
S = 4·½·ab + c² = 2ab + c²
S = (a + b)² = a² + b² +2ab
a² + b² = c²
c²

Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём.
Теорема в стихах

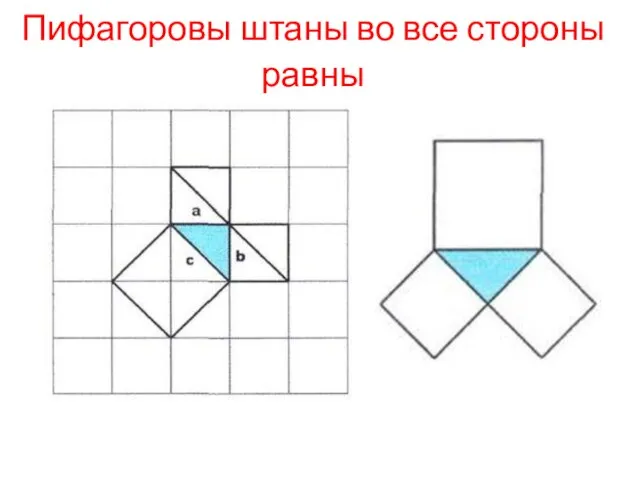
Пифагоровы штаны во все стороны равны

Шаржи

Сонет Шамиссо
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет
Быки ревут, её почуя, вслед.
Они не в силах свету помешать,
А могут лишь закрыв глаза дрожать
От страха, что вселил в них Пифагор.

Натягиаватели веревок
Гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3,4 и 5. Они брали веревку длиною в 12 м и привязывали по цветной полоске на расстоянии 3м от одного конца и 4м от другого конца. Прямой угол окажется заключенным между сторонами 3м и 4м.

Задача индийского математика
XII века Бхаскары
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

Задача из китайской
«Математики в девяти книгах»
«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?»

Задача из учебника «Арифметика» Леонтия Магницкого
«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обрете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».