Нобелевская премия по экономике

?
John Nash
основоположник теории некооперативных игр,
лауреат нобелевской премии
по экономике 1994
Russel Crowe
“Beautiful Mind”
2001
Lloyd Shapley
Основоположник теории кооперативных игр,
лауреат нобелевской премии
по экономике 2012

Кооперативные игры
Пусть N - множество игроков , n - их количество .
Определение Коалиция – подмножество множества игроков.
Большая (Гранд) коалиция –множество N всех игроков.
Характеристическая функция игры.
Отображение из множества всех коалиций в множество действительных чисел.
Характеристическая функция каждой коалиции ставит в соответствие совместный заработок ее членов.
Характеристическая функция в принципе может быть отрицательной (распределение затрат), но чаще она неотрицательная.
Пустая коалиция ничего не зарабатывает и никому ничего не должна,
Большая
коалиция

Пример. У Пети и Васи есть по одному кроссовку, а у Коли шнурки.
Один кроссовок ничего не стоит.
Пара кроссовок без шнурков стоит 300 грн.
Пара кроссовок со шнурками стоит 350 грн.
Шнурки можно продать отдельно за 20 грн.
V(П)=V(В)=0, V(К)=20, V(П,В)=300,
V(П,К)=V(В,К)=20, V(П,В,К)=350
Интуитивно ясно, что Пете, Васе и Коле надо объединиться, продать весь комплект и поделить деньги. Но как?

К

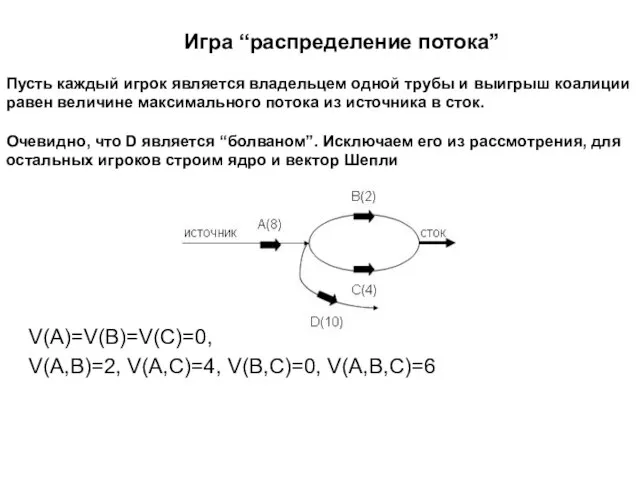
Игра “распределение потока”
Пусть каждый игрок является владельцем одной трубы и выигрыш коалиции равен величине максимального потока из источника в сток.
Очевидно, что D является “болваном”. Исключаем его из рассмотрения, для остальных игроков строим ядро и вектор Шепли
V(A)=V(B)=V(C)=0,
V(A,B)=2, V(A,C)=4, V(B,C)=0, V(A,B,C)=6

Здесь АВС сливается с АСВ, а ВСА с СВА.
В результате ядро – паралелограмм c вершинами
(2,0,4), (0,2,4), (4,2,0), (6,0,0).
Вектор Шепли (3,1,2) –
центр паралелограмма
х1
В.Ш. (3,1)
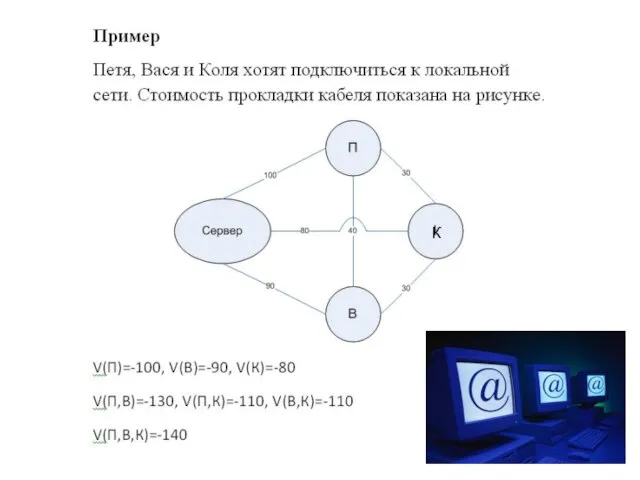
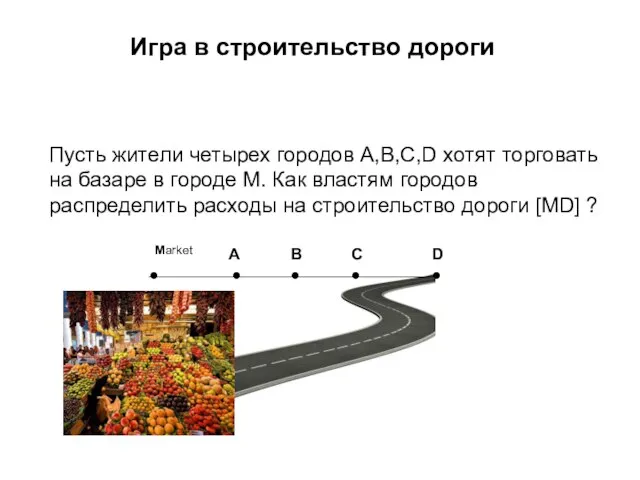
Проекция ядра на плоскость (x1,x2)

Пусть жители четырех городов А,B,C,D хотят торговать на базаре в городе M. Как властям городов распределить расходы на строительство дороги [MD] ?
Игра в строительство дороги

Ответ:
[MA] вскладчину строят A,B,C,D
[AB] – B,C и D
[BC] –C и D
[CD] – D строит самостоятельно
Концепция Шепли – для данной перестановки городов каждый город строит нужный ему участок дороги, если он еще не построен
Вектор Шепли совпадает с ответом

Задача о банкротстве
Как раздать долги кредиторам,
если долгов больше, чем денег?