Новый подход к решению систем уравнений в задачах дискретного логарифмирования

Криптографические системы, основанные на сложности дискретного логарифмирования
Схема открытого распределения ключей Диффи-Хеллмана
Схема ЭЦП Эль-Гамаля
ГОСТ Р34.10-2001(Россия)
ANSI X9.62/63-2001 (США)

Алгоритмы дискретного логарифмирования в конечных полях, использующие факторную базу
Алгоритм Адлемана
Алгоритм COS
Index-calculus
Решето числового поля
Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. - М.: МЦНМО, 2004 .

Постановка задачи
Решить систему n линейных уравнений c m неизвестными:
Операции сложения и умножения определены по правилам:
(здесь p - некоторое целое положительное число)

Сведение задачи к :
решению семейства систем над полями Галуа
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц
Анализ методов решения систем линейных уравнений в кольцах вычетов

Анализ методов решения систем линейных уравнений в кольцах вычетов
Сведение задачи к :
решению семейства систем над простыми полями
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц

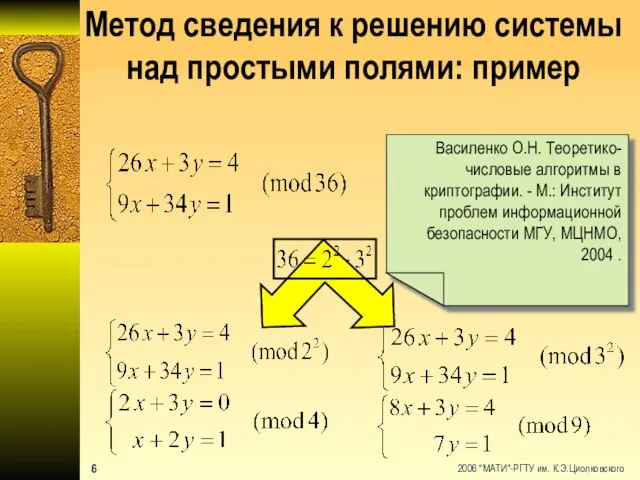
Метод сведения к решению системы над простыми полями: пример
Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. - М.: Институт проблем информационной безопасности МГУ, МЦНМО, 2004 .

Метод сведения к решению системы над простыми полями: пример (продолжение)
1
2

Метод сведения к решению системы над простыми полями: пример (продолжение)
1
2
3

Метод сведения к решению системы над простыми полями: пример (продолжение)
3
2
1

Метод сведения к решению системы над простыми полями: пример (продолжение)
По Китайской теореме об остатках:

Недостатки метода сведения к решению семейства систем над простыми полями
Решение не одной, а нескольких систем
Факторизация числа p: открытая проблема современной теории чисел (не существует алгоритма с полиномиальной сложностью)

Анализ методов решения систем линейных уравнений в кольцах вычетов
Сведение задачи к :
решению семейства систем над простыми полями
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц

Метод сведения к решению системы над кольцом целых чисел (1): пример
Сведение:
Общее решение:
экспоненциальный рост коэффициентов
Ноден П., Китте К. Алгебраическая алгоритмика. Пер. с франц. - М.: Мир, 1999.

Метод сведения к решению системы над кольцом целых чисел (2): модификации
Способы избежать экспоненциального роста коэффициентов:
Использование диагональной формы Смита
Модификация метода Гаусса
Недостаток:
Асимптотическая временная и емкостная сложность значительно больше сложности метода Жордана решения систем в полях Галуа
Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная алгебра: Учебник. - Нижегородский Государственный Университет им. Н.И. Лобачевского. – 2002.
Полиномиальный рост коэффициентов

Анализ методов решения систем линейных уравнений в кольцах вычетов
Сведение задачи к :
решению семейства систем над простыми полями
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц

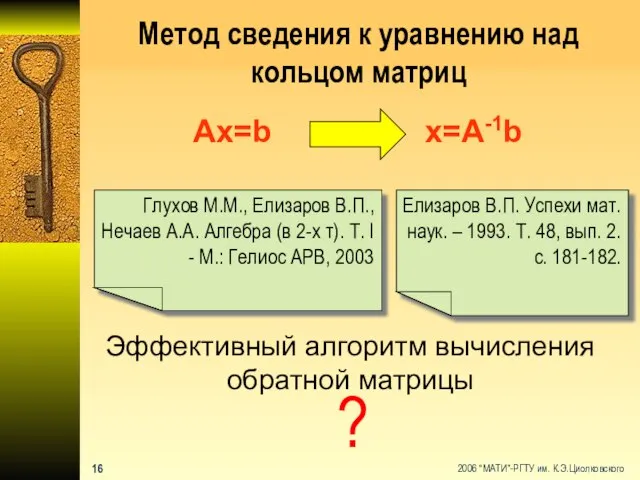
Метод сведения к уравнению над кольцом матриц
Ax=b
x=A-1b
Елизаров В.П. Успехи мат. наук. – 1993. Т. 48, вып. 2. с. 181-182.
Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра (в 2-х т). Т. I - М.: Гелиос АРВ, 2003

Предложенный метод
В основе:
Расширенный алгоритм Евклида
Схема Жордана
Применим для:
колец вычетов
полей Галуа
Эффективность:
По временной и емкостной сложности эквивалентен классическим алгоритмам Жордана и Гаусса решения систем в полях Галуа

Расширенный алгоритм Евклида
АЛГ Евклид(a,b)
ПОКА ЦИКЛ
К.Ц.
К.АЛГ.
Вход:
Выход: d, x, y, r, s такие, что

Схема Жордана

Матрицы над кольцом
Опр.2 Матрица называется строчно эквивалентной матрице если она может быть получена из A с помощью конечной последовательности элементарных преобразований строк.
Элементарными преобразованиями строк матрицы называют:
умножение любой ее строки на обратимый элемент кольца R;
прибавление к любой ее строке другой строки, умноженной на произвольный элемент кольца R;
транспозицию строк.
Опр.1 Множество всех матриц размером m x n с элементами из кольца R будем обозначать через Rm,n

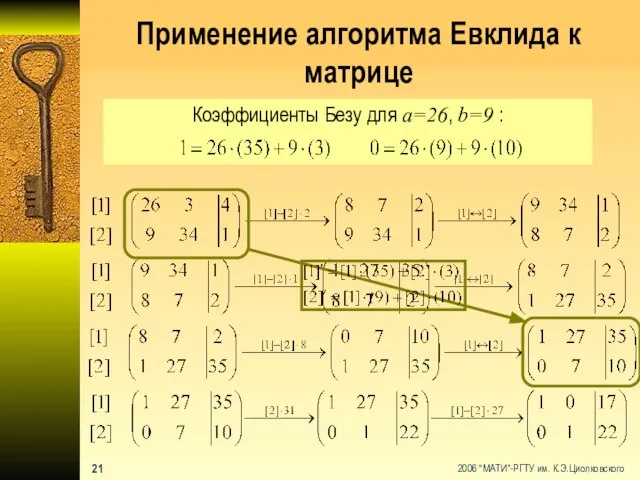
Применение алгоритма Евклида к матрице

Работа алгоритма
Решение системы:
Вычисление обратной матрицы:

Алгоритм
АЛГ Жордан(А, n, m, p)
ДЛЯ i=1 ДО n ЦИКЛ
{обнуляем эл-ты i-го столбца ниже i-й строки}
ДЛЯ j=i+1 ДО n ЦИКЛ
К.Ц. {для j}
Вход: {расширенная матрица}
Выход: А {преобразованная матрица}

Алгоритм (продолжение)
ЕСЛИ НОД(aii, p)>1
ТО выйти из алгоритма {матрица вырождена}
ИНАЧЕ {обнуляем элементы i-го столбца выше i-й строки}
К.Е.
ВЕРНУТЬ(А)
К.АЛГ.

Временная сложность алгоритмов
Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная алгебра: Учебник. - Нижегородский Государственный Университет им. Н.И. Лобачевского. – 2002.
Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра
(в 2-х т). Т. I - М.: Гелиос АРВ, 2003
Елизаров В.П. Успехи мат. наук.–1993.Т. 48, вып. 2.
Метод сведения к уравнению над кольцом матриц
Метод сведения к диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе
Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. - М.: Институт проблем информационной безопасности МГУ,
МЦНМО, 2004
Авдошин С.М., Савельева А.А. Свид. Об официальной регистрации программы для ЭВМ № 2005612258: «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ 02.09.2005

Временная сложность алгоритмов
Авдошин С.М., Савельева А.А. Свид. Об официальной регистрации программы для ЭВМ № 2005612258: «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ 02.09.2005
Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная алгебра: Учебник. - Нижегородский Государственный Университет им. Н.И. Лобачевского. – 2002.
Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра
(в 2-х т). Т. I - М.: Гелиос АРВ, 2003
Елизаров В.П. Успехи мат. наук.–1993.Т. 48, вып. 2.
Метод сведения к уравнению над кольцом матриц
Метод сведения к диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе

Временная сложность алгоритмов
Авдошин С.М., Савельева А.А. Свид. Об официальной регистрации программы для ЭВМ № 2005612258: «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ 02.09.2005
Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра
(в 2-х т). Т. I - М.: Гелиос АРВ, 2003
Елизаров В.П. Успехи мат. наук.–1993.Т. 48, вып. 2.
Метод сведения к уравнению над кольцом матриц
Метод сведения к диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе

Временная сложность алгоритмов
Авдошин С.М., Савельева А.А. Свид. Об официальной регистрации программы для ЭВМ № 2005612258: «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ 02.09.2005
Метод сведения к уравнению над кольцом матриц
Метод сведения к диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе

Временная сложность алгоритмов
Метод сведения к уравнению над кольцом матриц
Метод сведения к диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе

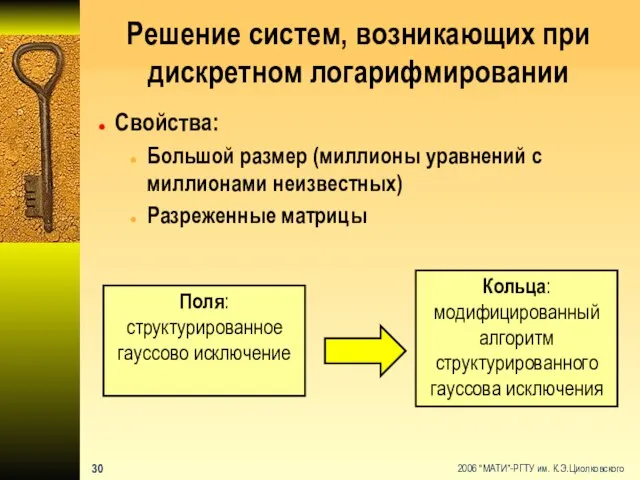
Решение систем, возникающих при дискретном логарифмировании
Свойства:
Большой размер (миллионы уравнений с миллионами неизвестных)
Разреженные матрицы
Поля: структурированное гауссово исключение
Кольца: модифицированный алгоритм структурированного гауссова исключения

Заключение
Результаты, полученные в данной работе:
Проведен анализ известных методов решения систем линейных уравнений над кольцом вычетов
Разработан алгоритм, эквивалентный по сложности методам Жордана и Гаусса решения систем линейных уравнений над полями Галуа
Программа, реализующая разработанный алгоритм, зарегистрирована Федеральной службой по интеллектуальной собственности, патентам и товарным знакам (Роспатент)
Результаты исследований опубликованы в журнале «Информационные технологии» (№2, 2006)

Направление дальнейшей работы
Теоретическое и экспериментальное исследование влияния полученного метода на временную сложность алгоритмов дискретного логарифмирования, использующие факторную базу:
Алгоритм Адлемана
Index-calculus
Алгоритм COS
Решето числового поля

Кольца вычетов
Операции сложения и умножения определяют кольцо вычетов по модулю p . Оно является коммутативным кольцом с единицей.
Опр.1 Делителем нуля в произвольном кольце R называется любой его элемент для которого в R существует элемент удовлетворяющий условию a ·b=0 или b ·a=0
Опр.2 Обратимым элементом в произвольном кольце R называется любой его элемент для которого в R существует обратный элемент a-1, удовлетворяющий условию a · a-1 =1 или a-1 ·a=1

Обратный элемент
Элемент называется обратным к , если
Для нахождения обратного элемента нужно решить линейное диофантово уравнение:
Уравнение разрешимо относительно u и v тогда и только тогда, когда НОД(x,p)=1; в этом случае Для вычисления u и v (коэффициентов Безу) используется расширенный алгоритм Евклида.

Пример решения системы в поле Галуа порядка 37