Содержание
- 2. Раздел 1 Общая теория статистики Тема 1. Предмет, метод и задачи общей теории статистики Тема 2.
- 3. Тема 1. Предмет, метод и задачи общей теории статистики 1.1. Предмет общей теории статистики 1.2. Основные
- 4. 1.1. Предмет общей теории статистики
- 5. Изначально термин «статистика» (происходит от лат. status - состояние, положение вещей) употреблялся в значении «политическое состояние»
- 6. Уильям Петти (Petty) - английский экономист, родоначальник буржуазной классической политической экономии. Получил медицинское образование в университетах
- 7. Адольф Кетле (Lambert-Adolph-Jacques Quetelet) главным образом известен как отец современной статистики. Посетив Англию, Шотландию, Швейцарию, Италию
- 8. Первый русский профессор и член Петербургской Академии наук, человек энциклопедических знаний, разносторонних интересов и способностей. В
- 9. Из данного определения следуют основные черты предмета статистической науки: 1. Статистика - наука общественная. 2. В
- 10. 1.2. Основные понятия теории статистики
- 11. 1. Статистическая совокупность – это множество единиц изучаемого явления, объединенных в соответствии с задачей исследования единой
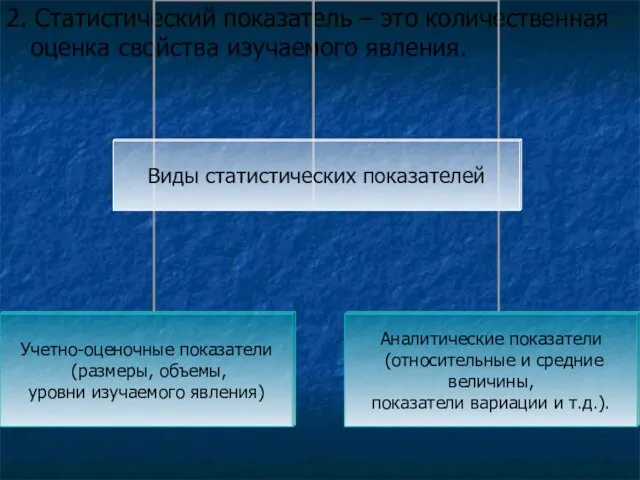
- 12. 2. Статистический показатель – это количественная оценка свойства изучаемого явления.
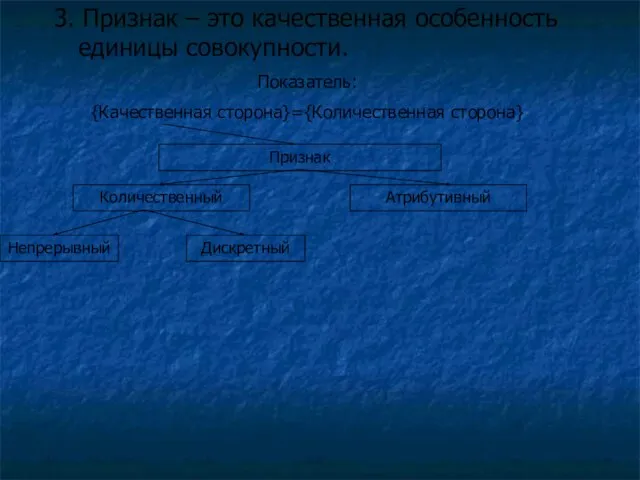
- 13. 3. Признак – это качественная особенность единицы совокупности. Показатель: {Качественная сторона}={Количественная сторона} Признак Количественный Атрибутивный Непрерывный
- 14. 4. Статистическая закономерность - это форма проявления причинной связи, выражающаяся в последовательности, регулярности, повторяемости событий с
- 15. 1.3. Стадии и методы статистического исследования
- 16. Статистическое исследование количественной стороны общественных явлений проходит три стадии. 1. Сбор первичной статистической информации. На этой
- 17. 1.4. Задачи статистики
- 18. На каждом этапе развития перед статистикой встают специфические задачи, обусловленные характером самого этапа. В условиях рыночной
- 19. Особое внимание должно быть уделено совершенствованию методологии анализа важнейших пропорций: между производством и потреблением, потреблением и
- 20. Практическое решение этих задач призвана осуществлять система органов государственной статистики. Конкретные задачи определены: Гражданским кодексом Российской
- 21. В постановлении Правительства РФ от 30 июля 2004 г. отмечается, что Федеральная служба государственной статистики (далее
- 22. С целью реализации полномочий в установленной сфере деятельности Федеральная служба государственной статистики имеет право: запрашивать и
- 23. Федеральная служба государственной статистики http://www.fsgs.ru/
- 24. Тема 2. Массовые статистические наблюдения 2.1. Основные требования, предъявляемые к массовым статистическим наблюдениям 2.2.Основные организационные формы,
- 25. 2.1. Основные требования, предъявляемые к массовым статистическим наблюдениям Точность и достоверность. Полнота в отношении охвата данных:
- 26. 2.2.Основные организационные формы, виды и способы статистического наблюдения
- 27. В российской статистике используются три основные организационные формы статистического наблюдения: Статистическая отчетность (предприятий, организаций, учреждений и
- 28. В практике статистики различают регистры населения и регистры предприятий. Регистр населения - поименованный и регулярно актуализируемый
- 29. Виды статистического наблюдения классифицируются по следующим признакам: ■ времени регистрации фактов: непрерывное (текущее), периодическое и единовременное;
- 30. Способами статистического наблюдения являются непосредственное наблюдение (замер, подсчет); документальный учет фактов (необходимые сведения берутся из соответствующих
- 31. 2.3. Организационный план статистического наблюдения
- 33. 2.4. Ошибки статистического наблюдения
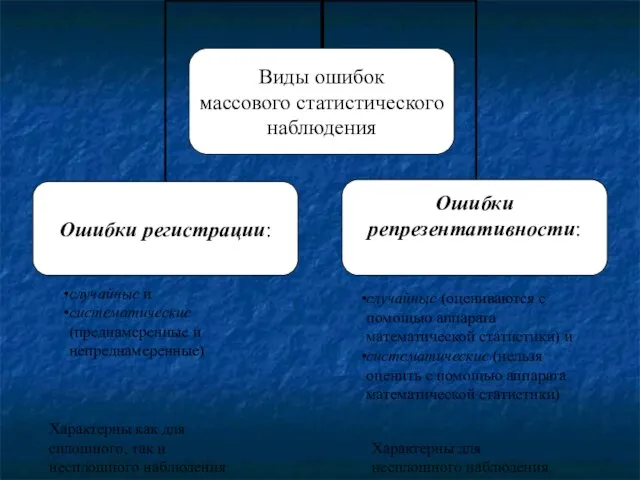
- 34. Ошибки регистрации - это отклонения между значением показателя, полученным в ходе статистического наблюдения, и фактическим, действительным
- 35. случайные и систематические (преднамеренные и непреднамеренные) случайные (оцениваются с помощью аппарата математической статистики) и систематические (нельзя
- 36. После получения статистических формуляров следует провести проверку полноты и качества собранных данных. Контроль полноты - это
- 37. Тема 3. Сводка и группировка статистических данных. Статистические таблицы
- 38. Программа сводки включает определение: групп и подгрупп; системы показателей; видов таблиц. С помощью метода группировок решаются
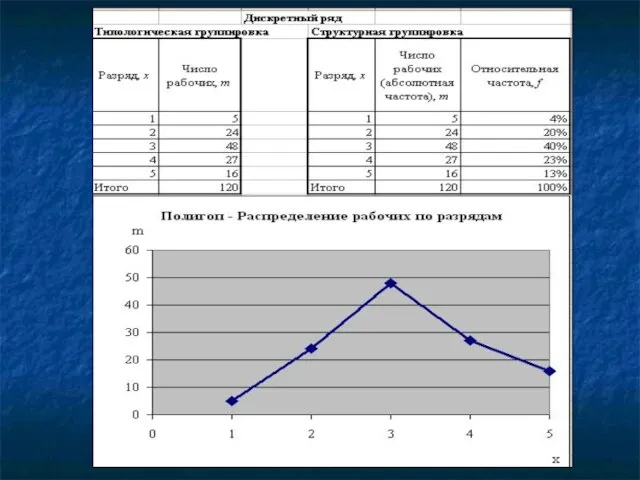
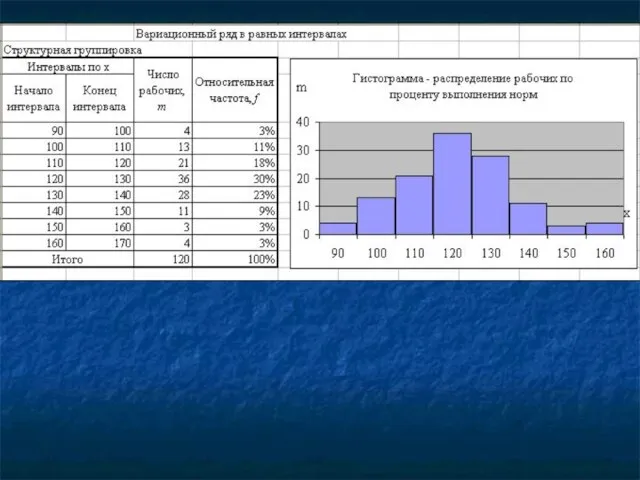
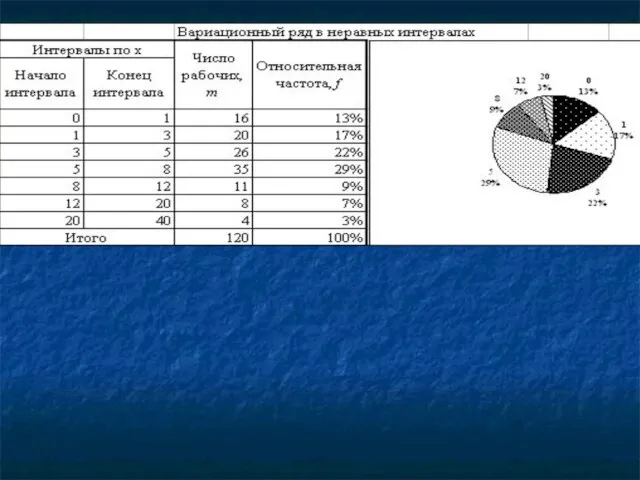
- 39. Группировка – это разбиение совокупности на группы, однородные по какому-либо признаку. Классификация – это узаконенная, общепринятая,
- 40. Для определения число групп с используется формула Стерджесса: n = 1 + 3,322 lgN, где n
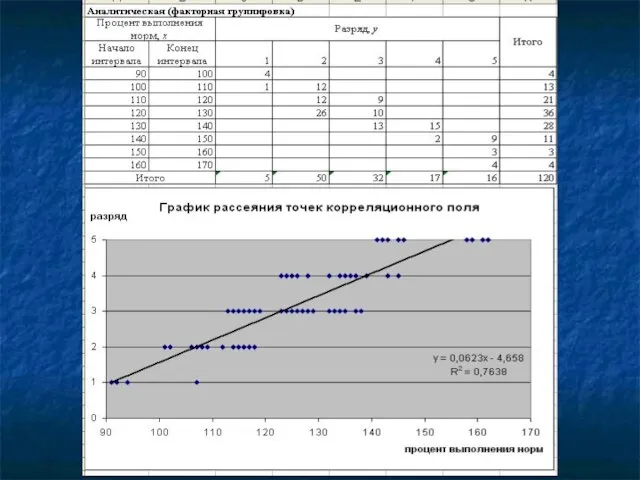
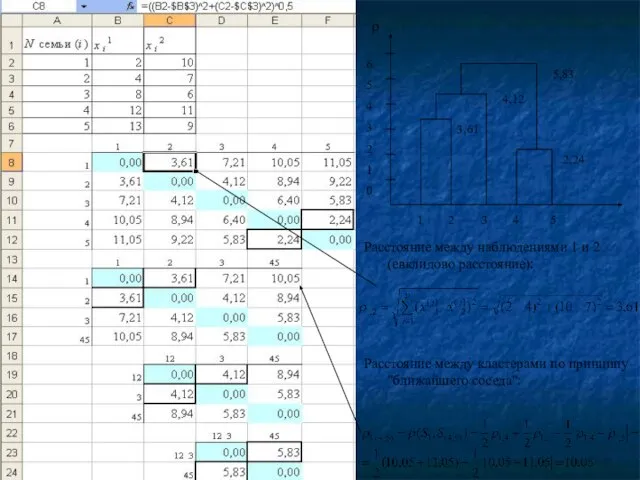
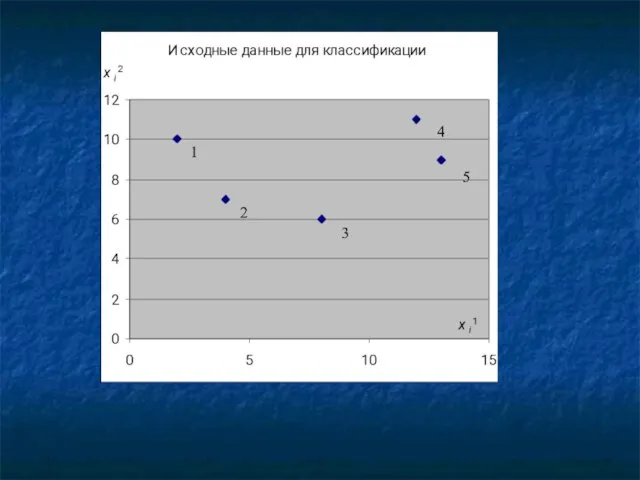
- 46. Методы многомерной классификации. Кластерный анализ Claster (англ.) – группа элементов, характеризуемых каким-либо общим свойством Пример Провести
- 47. Расстояние между наблюдениями 1 и 2 (евклидово расстояние): Расстояние между кластерами по принципу "ближайшего соседа": 6
- 48. 1 2 3 4 5
- 49. Тема 4. Абсолютные и относительные величины
- 50. А. Абсолютные величины отражают физические размеры изучаемых статистикой процессов и явлений, а именно их массу, площадь,
- 51. 1. Относительная величина динамики (ОВД) - отношение уровня исследуемого процесса или явления за данный период времени
- 52. Пример 1
- 53. 2. Относительная величина расчетного задания (ОВРз) - отношение величины расчетного задания на период к достигнутой величине
- 54. ОВРз·ОВРвз=ОВД Пример 2
- 55. 4. Относительная величина структуры (ОВС) - соотношение структурных частей изучаемого объекта и их целого:
- 56. Пример 3 На основании данных примера 1 рассчитать относительные величины структуры
- 57. 5. Относительная величина координации (ОВК) - отношение одной части совокупности к другой части этой же совокупности:
- 58. Пример 4 На основании данных примера 1 рассчитать относительные величины координации
- 59. 6. Относительная величина интенсивности (ОВИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение
- 60. Пример 5
- 61. 7. Относительная величина сравнения (ОВСр) - соотношение одного и того же абсолютного показателя, характеризующего разные объекты:
- 62. Пример 6
- 63. Тема 5. Анализ рядов распределения 5.1. Средние величины 5.2. Анализ вариации 5.3. Анализ формы кривой распределения
- 64. Основные стадии анализа рядов распределения: Оценка массового уровня признака с помощью расчета средних показателей. Оценка колеблемости
- 65. 5.1. Средние величины 5.1.1. Принципы применения средних величин 5.1.2. Классификация средних величин 5.1.3. Степенные средние 5.1.4.
- 66. 5.1.1. Принципы применения средних величин При определении средней в каждом конкретном случае нужно исходить из качественного
- 67. 5.1.2. Классификация средних величин
- 68. 5.1.3. Степенные средние
- 69. Простая средняя считается по несгруппированным данным: Взвешенная средняя считается по сгруппированным данным: =n
- 71. Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся
- 72. В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в % или долях
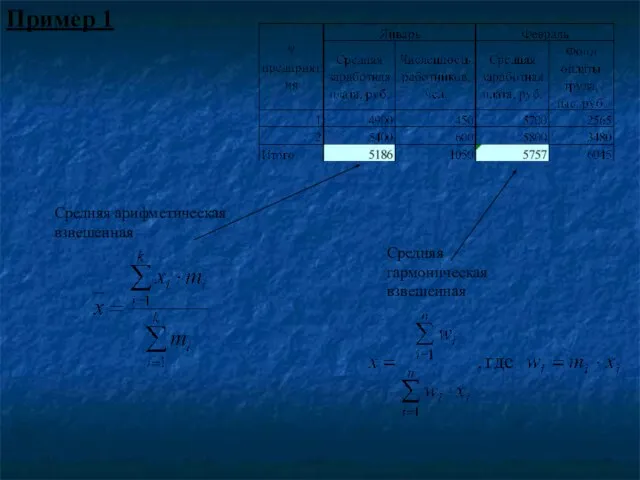
- 73. Пример 1 Средняя арифметическая взвешенная Средняя гармоническая взвешенная
- 74. Пример 2
- 75. Пример 3
- 76. Пример 4 Финансирование инвестиций за счет собственных средств по предприятиям АО за отчетный период характеризуются следующими
- 77. Пример 5 Портфель инвестора состоит из акций трех компаний. Их доходность равна соответственно 15, 18 и
- 78. Пример 6
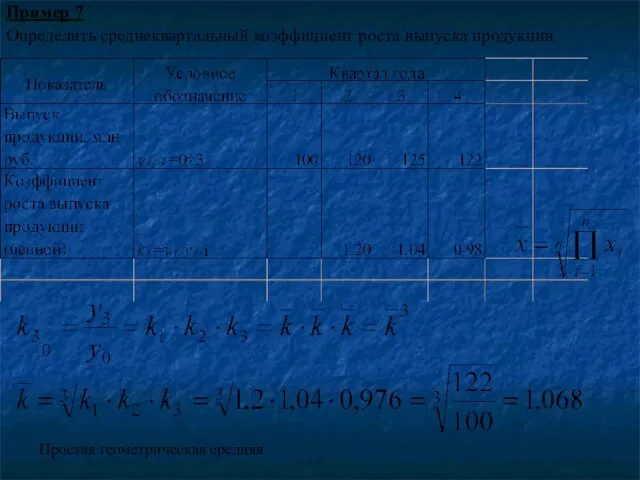
- 79. Пример 7 Определить среднеквартальный коэффициент роста выпуска продукции. Простая геометрическая средняя
- 80. Пример 8 Определить среднегодовой темп роста душевого дохода в США в рассматриваемом периоде. Взвешенная геометрическая средняя
- 81. 5.1.4. Структурные средние
- 82. Мода (Мо) - наиболее часто встречающееся значение признака в совокупности.
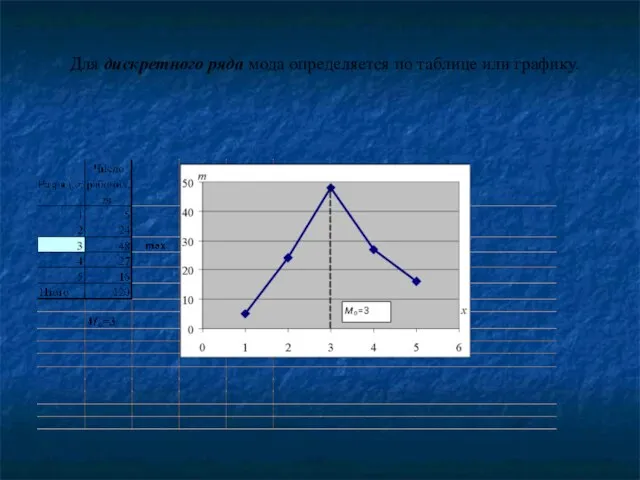
- 83. Для дискретного ряда мода определяется по таблице или графику.
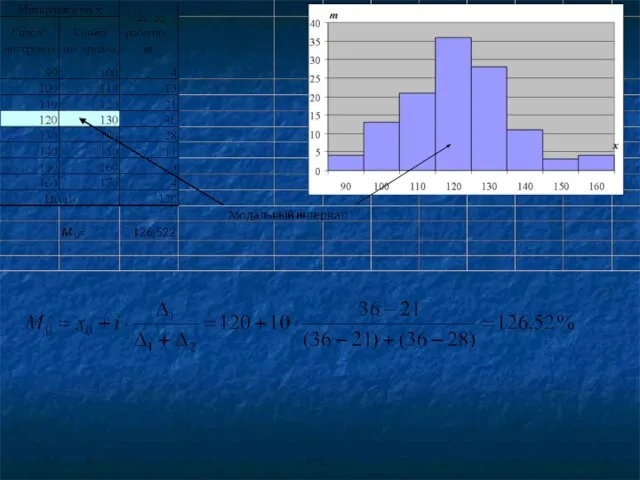
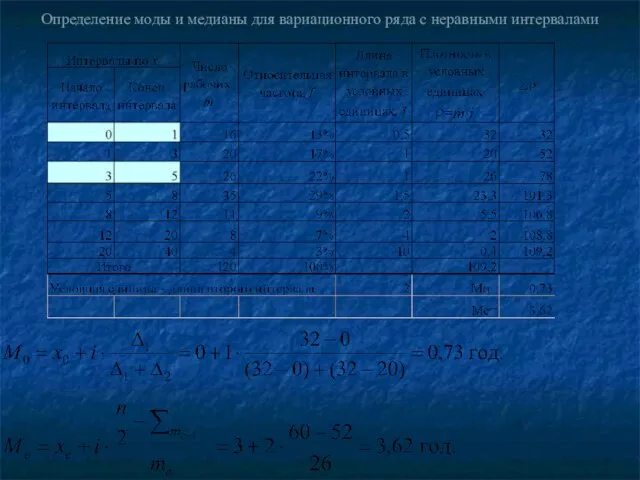
- 84. Для интервального ряда мода определяется в два этапа: определяется модальный интервал; уточняется значение моды внутри модального
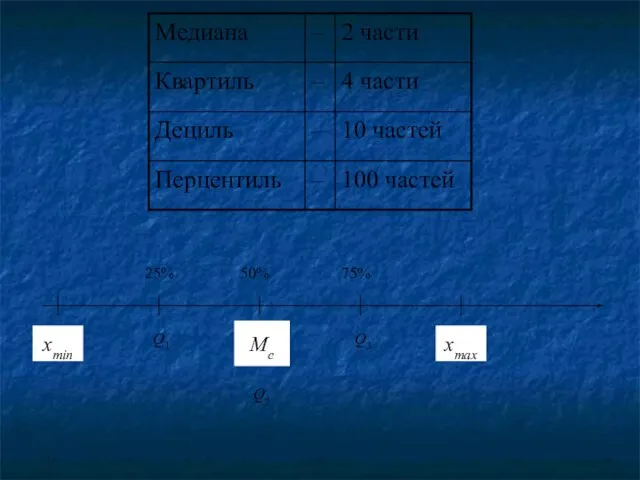
- 86. 2. Медиана (Ме) – значение признака в середине ранжированного ряда. Определение медианы для несгруппированных данных
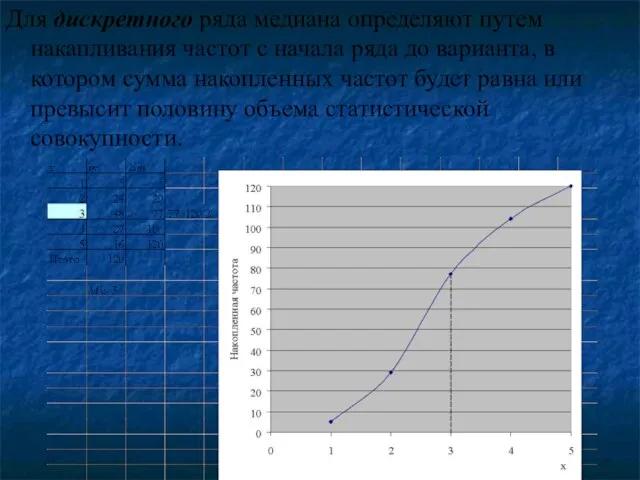
- 87. Для дискретного ряда медиана определяют путем накапливания частот с начала ряда до варианта, в котором сумма
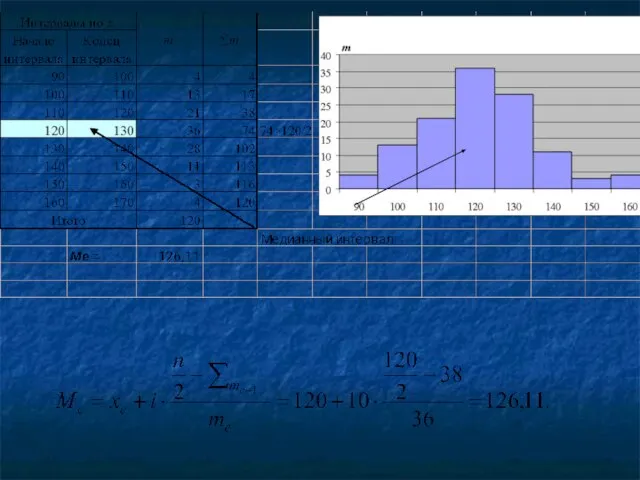
- 88. Для интервального ряда медиана определяется в два этапа: определяется медианный интервал; уточняется значение медианы внутри медианного
- 90. Определение моды и медианы для вариационного ряда с неравными интервалами
- 91. xmin xmax Me Q3 Q2 Q1 50% 75% 25%
- 92. 5.2. Анализ вариации
- 93. Колеблемость отдельных значений характеризуют показатели вариации. Термин «вариация» произошел от латинского variatio - изменение, колеблемость, различие.
- 97. Простейшие свойства σ Если все частоты умножить или разделить на какое-либо постоянное число, то σ не
- 98. Чем меньше Vσ и σ, тем надежнее среднее. Условная граница однородности Vσ =33%.
- 99. Пример 1
- 100. Пример 2
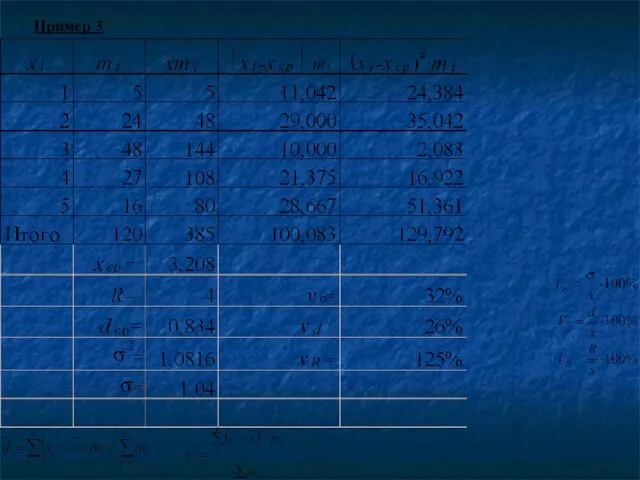
- 101. Пример 3
- 102. Правило сложения дисперсий Если некоторая совокупность единиц делится на группы, то наряду с общей дисперсией могут
- 103. В математической статистике доказывается, что общая дисперсия равна: Средняя из групповых дисперсий Межгрупповая дисперсия
- 104. Пример 4
- 105. 5.3. Анализ формы кривой распределения
- 106. При построения кривой распределения выделяют два подхода: Прямой, который заключается в постепенном уменьшении величины интервалов и
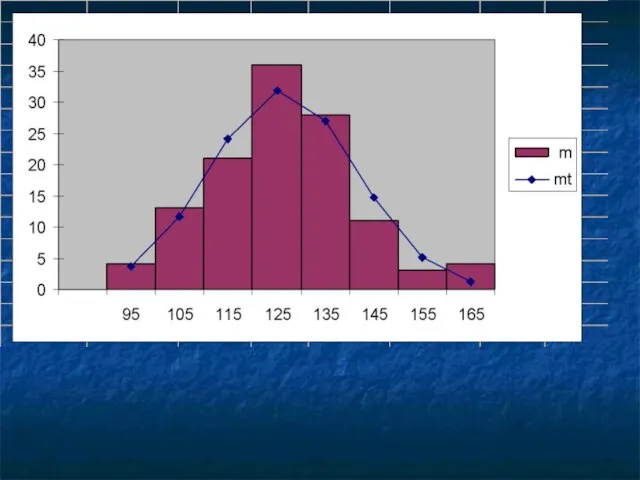
- 107. Математическое выравнивание сводится к отысканию кривой распределения, которая отражает закономерность изменения плотности в чистом виде. Математической
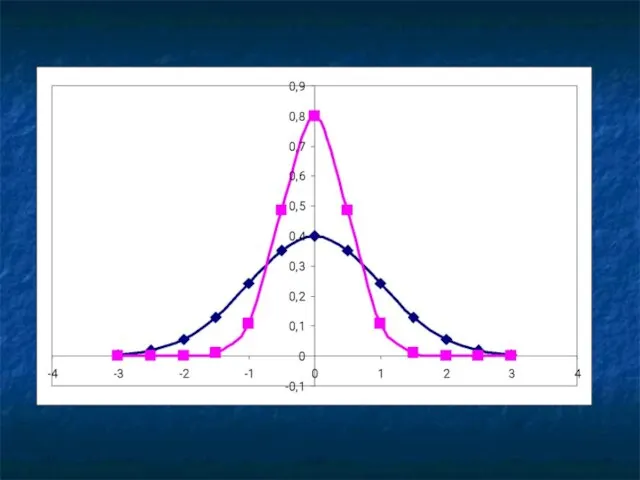
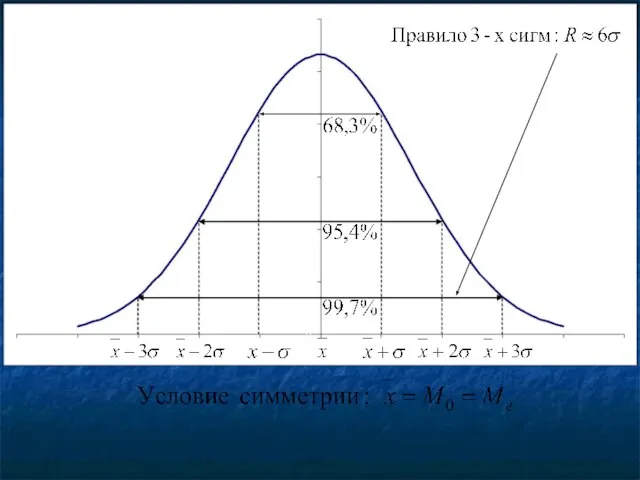
- 108. Нормальное распределение Условие его возникновения: Если интересующий нас признак формируется под влиянием суммарного действия взаимонезависимых факторов,
- 109. Нормальное распределение Гаусса-Ляпунова выражается следующей формулой:
- 110. Заменив через , переходим к стандартной системе единиц, где начало отсчета , а единица измерения .
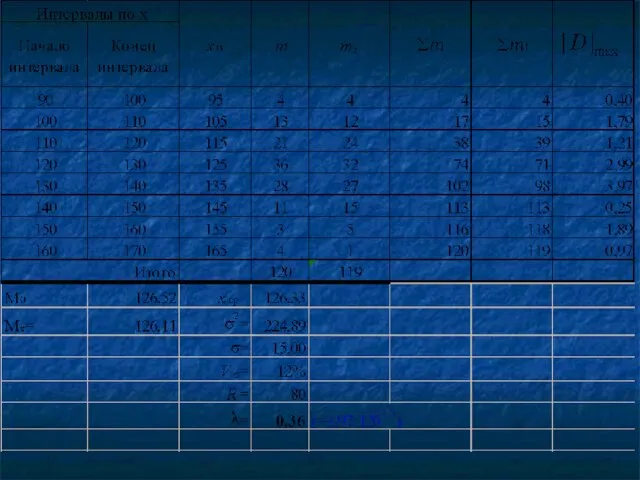
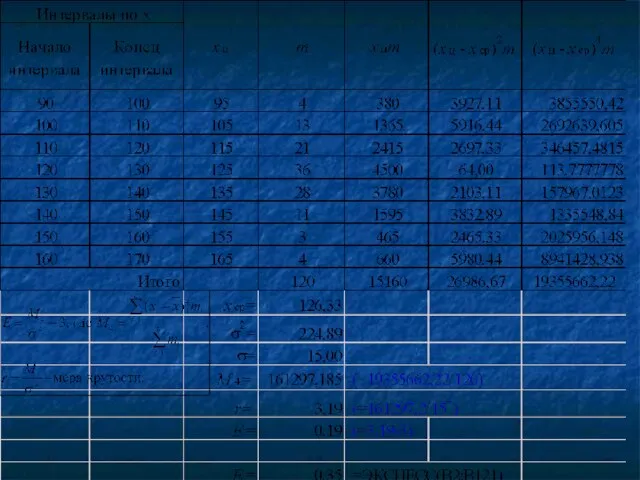
- 112. Выравнивание эмпирического ряда распределения по нормальной кривой осуществляется в следующей последовательности. 1. Определить центры интервалов в
- 115. Критерий Колмогорова Несовпадения между эмпирическим и теоретическим (по нормальному закону) рядами распределения обусловлены двумя причинами: расхождения
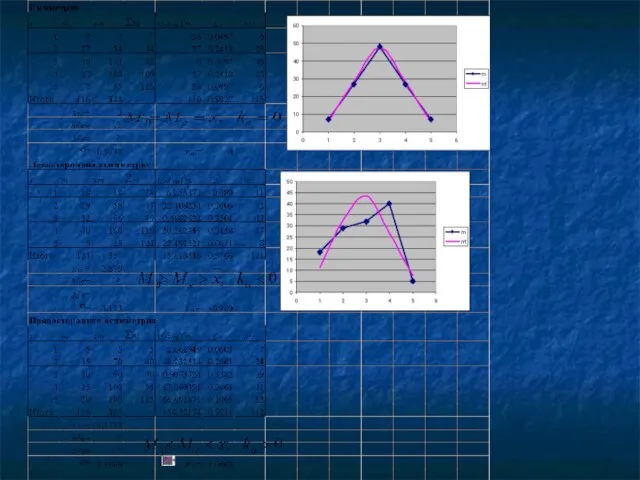
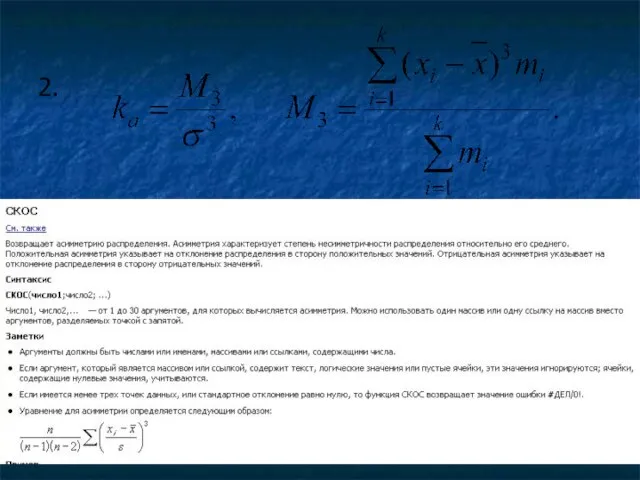
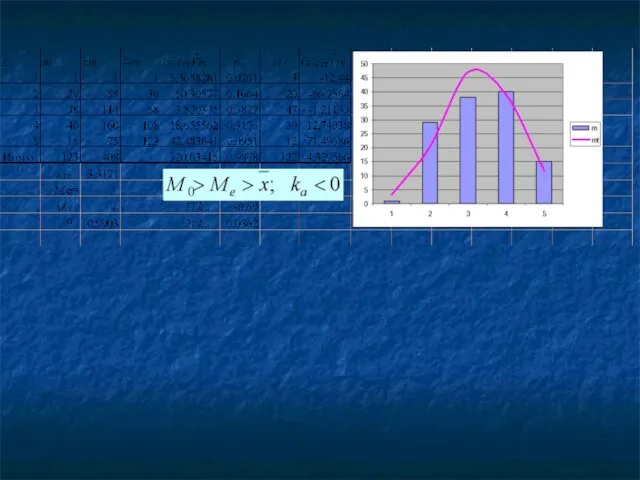
- 118. Асимметрия распределения Два варианта оценки степени асимметрии: Коэффициент асимметрии При левосторонней (отрицательной) асимметрии: При правосторонней (положительной)
- 120. 2.
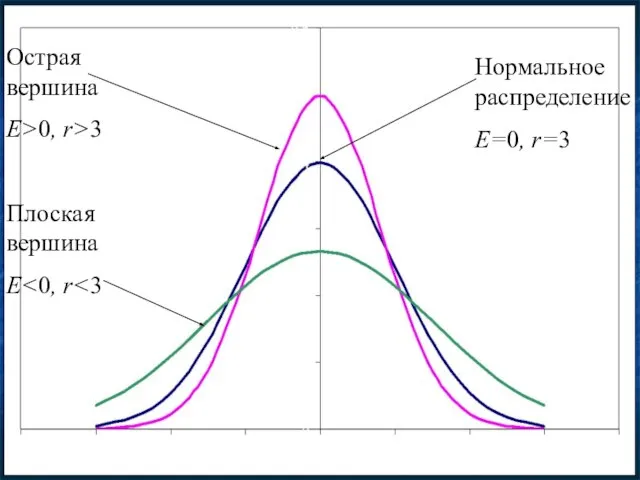
- 122. Эксцесс Используется для характеристики островершинности кривой распределения. Определяется по формуле:
- 123. Нормальное распределение E=0, r=3 Острая вершина E>0, r>3 Плоская вершина E
- 126. Скачать презентацию































































































 Евстафьев А.И. Начальник отдела консалтинга ООО “Южная Юридическая Консалтинговая Компания”, САРН Максимов Д.В. Финансовый дире
Евстафьев А.И. Начальник отдела консалтинга ООО “Южная Юридическая Консалтинговая Компания”, САРН Максимов Д.В. Финансовый дире Базовая станция МегаФон
Базовая станция МегаФон Матюшевский Дом культуры приглашение в дни весенних праздников
Матюшевский Дом культуры приглашение в дни весенних праздников Бизнес инсайт. Саша Лонго. Как стать человеком-магнитом
Бизнес инсайт. Саша Лонго. Как стать человеком-магнитом Полевые транзисторы. Самостоятельная работа
Полевые транзисторы. Самостоятельная работа МОНИТОРЫ
МОНИТОРЫ Важнейшие географические открытия. Марко Поло и его путешествия.
Важнейшие географические открытия. Марко Поло и его путешествия. Уголовно - правовые отношения
Уголовно - правовые отношения Создание базы знаний по флоре Байкальской Сибири
Создание базы знаний по флоре Байкальской Сибири Наброски и зарисовки архитектурных строений и их элементов. Пленэр
Наброски и зарисовки архитектурных строений и их элементов. Пленэр Кому нужен ВСД. Комплексная транспортная система Санкт-Петербурга
Кому нужен ВСД. Комплексная транспортная система Санкт-Петербурга Традиции празднования Рождества в США
Традиции празднования Рождества в США Время любви - весна
Время любви - весна Презентация на тему ХАМЕЛЕОНЫ
Презентация на тему ХАМЕЛЕОНЫ  Formy prac florystycznych
Formy prac florystycznych Традиции семьи для квеста
Традиции семьи для квеста Как выполнить чертёж Брусок /стойка/. 10, 11 класс
Как выполнить чертёж Брусок /стойка/. 10, 11 класс Правовые символы
Правовые символы ОАО «РУСДЖАМ КИРИШИ»
ОАО «РУСДЖАМ КИРИШИ» 732 Вот год пришёл к кончине
732 Вот год пришёл к кончине Русская культура в конце XIII- начале XIV веков
Русская культура в конце XIII- начале XIV веков Порядок назначения и выплаты пособий семьям с детьми в РФ
Порядок назначения и выплаты пособий семьям с детьми в РФ КЕЙС. СТРАТЕГИЯ РОСТА
КЕЙС. СТРАТЕГИЯ РОСТА Я буду конструктором, проектировщиком или архитектором – детские мечты в реальность
Я буду конструктором, проектировщиком или архитектором – детские мечты в реальность Презентация на тему Функция и её график
Презентация на тему Функция и её график  ЖИВОПИСЬ 14 — 15 ВЕКОВ НА РУСИ
ЖИВОПИСЬ 14 — 15 ВЕКОВ НА РУСИ  #Pokupanda_Tomsk
#Pokupanda_Tomsk FEATURES OF DRUGS ACTION DURING PREGNANCY
FEATURES OF DRUGS ACTION DURING PREGNANCY