Содержание
- 2. Аннотация. Представленный урок является первым уроком-лекцией по теме «Объёмы». Компьютерные технологии позволяют сделать этот урок красочным
- 3. План урока 1.Повторение ранее изученного. 2.Объяснение нового материала: а) понятие объёма; б) свойства объёма; в) объём
- 4. О с н о в н а я ц е л ь у р о к
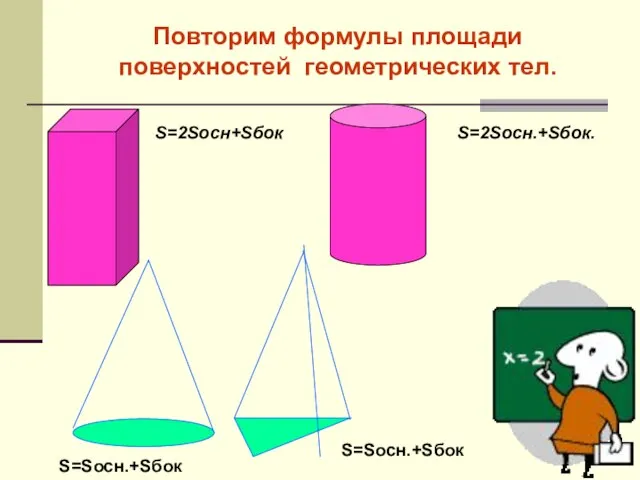
- 5. Повторим формулы площади поверхностей геометрических тел. S=2Sосн+Sбок S=2Sосн.+Sбок. S=Sосн.+Sбок S=Sосн.+Sбок
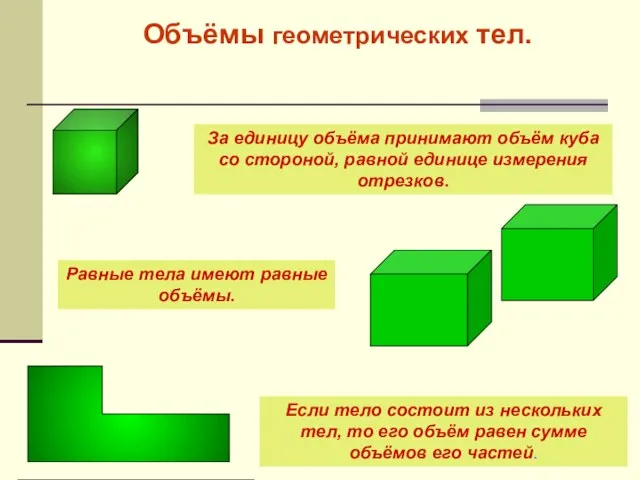
- 6. Объёмы геометрических тел. Равные тела имеют равные объёмы. За единицу объёма принимают объём куба со стороной,
- 7. Понятие объёма тела вводится по аналогии с понятием площади плоской фигуры. Заполним вторую половину таблицы.
- 8. Куб-частный случай прямоугольного параллелепипеда. Чему равен объём прямоугольного параллелепипеда? Объём прямоугольного параллелепипеда равен произведению трёх его
- 9. Контрольные вопросы. 1.Что называется объёмом тела? 2.Что значит измерить объём тела? 3.Что значит:»Объём комнаты 60 м3
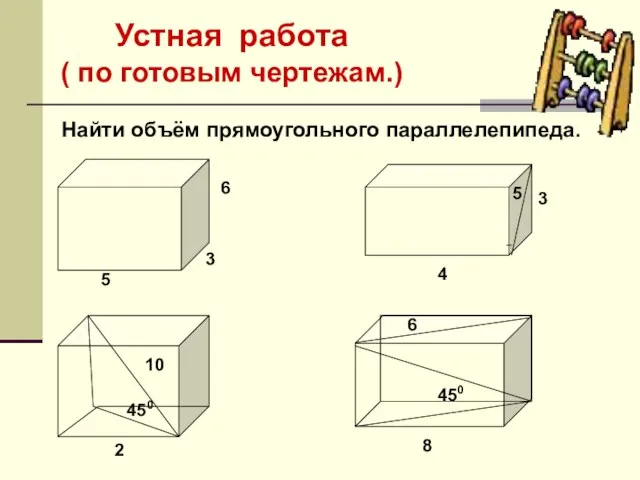
- 10. Устная работа ( по готовым чертежам.) Найти объём прямоугольного параллелепипеда. 450
- 11. Решение задач. 1.Площадь полной поверхности куба равна 6 м2. Найти его объём. 2.Объём куба равен 8
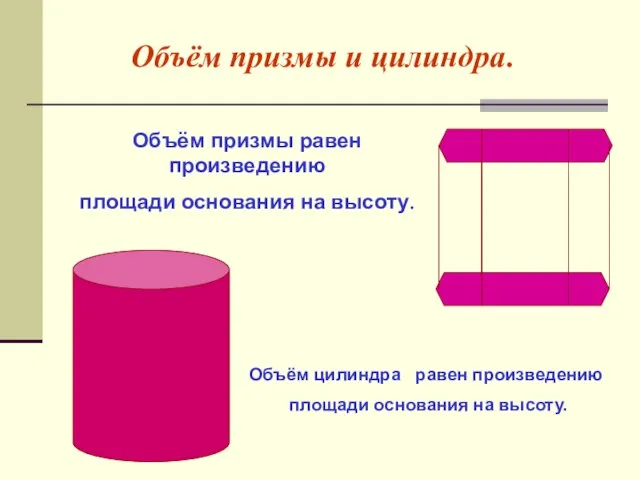
- 12. Объём призмы и цилиндра. Объём призмы равен произведению площади основания на высоту. Объём цилиндра равен произведению
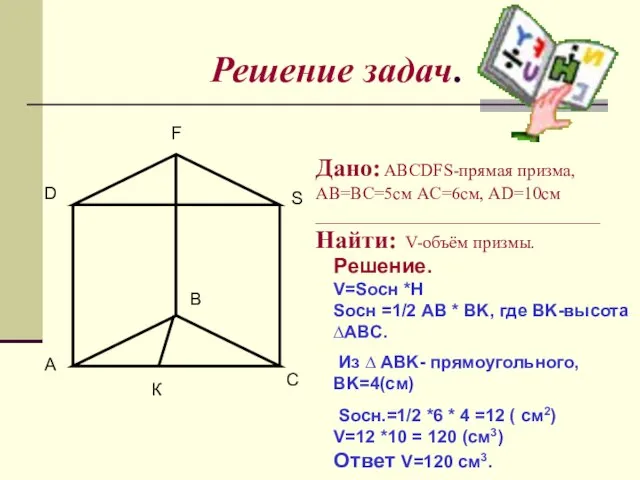
- 13. Решение задач. A B C D F S Дано: ABCDFS-прямая призма, AB=BC=5см AC=6см, AD=10cм ________________________________Найти: V-объём
- 14. Самостоятельная работа. Вариант-1. 1.Объём прямоугольного параллелепипеда равен 96 см3, боковое ребро 8 см.Чему равна площадь основания?
- 15. Л и т е р а т у р а . 1.Учебник «Геометрия 10-11 класс «
- 17. Скачать презентацию









 Проект. Русская архитектура XVIII века. Живопись и скульптура
Проект. Русская архитектура XVIII века. Живопись и скульптура Международный День белой трости
Международный День белой трости Юлия Трушина
Юлия Трушина Презентация к уроку русского языка в 6 классе по теме Буквы О-Ё после шипящих и Ц в суффиксах прилагательных
Презентация к уроку русского языка в 6 классе по теме Буквы О-Ё после шипящих и Ц в суффиксах прилагательных Клонирование
Клонирование Слабые люди считают, что наркотики могут помочь справиться с проблемами …
Слабые люди считают, что наркотики могут помочь справиться с проблемами … Висы и упоры
Висы и упоры Презентация на тему Натурфолософия
Презентация на тему Натурфолософия  Детский сад № 72 общеразвивающего вида
Детский сад № 72 общеразвивающего вида Основные разделы фикха
Основные разделы фикха Weather 2 класс
Weather 2 класс Алициклические соединения
Алициклические соединения  Лесоразведение как альтернатива существующим практикам хозяйствования и адаптация к меняющимся климатическим условиям на приме
Лесоразведение как альтернатива существующим практикам хозяйствования и адаптация к меняющимся климатическим условиям на приме За нами – Москва! 7 класс
За нами – Москва! 7 класс Геополитические интересы России в энергетической сфере в начале XXI века Гарегин Асланян
Геополитические интересы России в энергетической сфере в начале XXI века Гарегин Асланян Формирование уУД в начальной школе
Формирование уУД в начальной школе Славные символы России (4 класс)
Славные символы России (4 класс) Мелкий ремонт одежды. Пришивание пуговиц
Мелкий ремонт одежды. Пришивание пуговиц Пик Знаний
Пик Знаний  Источники финансирование бизнеса. Менеджмент . Маркетинг
Источники финансирование бизнеса. Менеджмент . Маркетинг Брызгалова Ольга Ивановна
Брызгалова Ольга Ивановна Крестьянство. Повседневный быт и обычаи Руси 17 века
Крестьянство. Повседневный быт и обычаи Руси 17 века Экономика
Экономика Тема: Имя прилагательное. Повторение.(Урок русского языка в 6-ом классе)
Тема: Имя прилагательное. Повторение.(Урок русского языка в 6-ом классе) Сложение и вычитание чисел в пределах 100
Сложение и вычитание чисел в пределах 100 Мастер – класс Осенние фантазии
Мастер – класс Осенние фантазии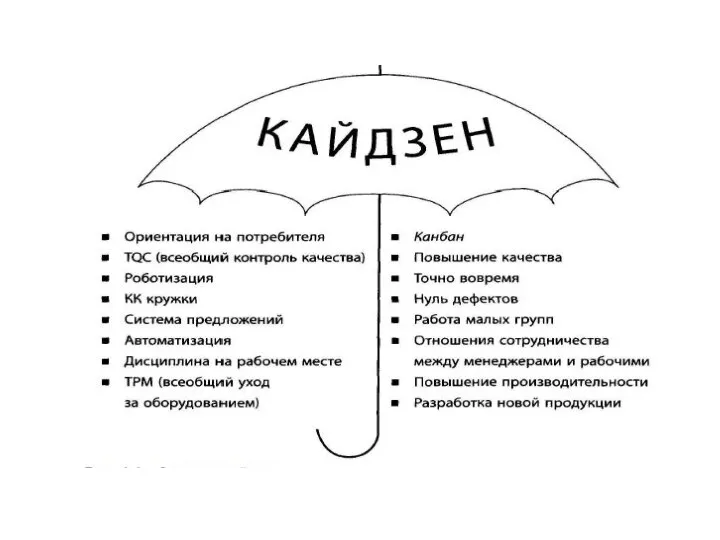 Кайдзен. Японское понимание распределения рабочих функций
Кайдзен. Японское понимание распределения рабочих функций Терразитовые штукатурки
Терразитовые штукатурки