Однофазные цепи синусоидального тока

Основные теоретические сведения
Переменный электрический ток – это ток, изменяющийся с течением времени.
Значение этой величины в рассматриваемый момент времени называется мгновенным значением тока i.
Продолжить

Наиболее распространен переменный синусоидальный ток, являющийся синусоидальной функцией времени.
Переменный синусоидальный сигнал характеризуется:
периодом Т, который выражается в секундах (с),
частотой f - величиной, обратной периоду, выражается в герцах (Гц).
круговой частотой ω = 2πf (1/с).
Продолжить

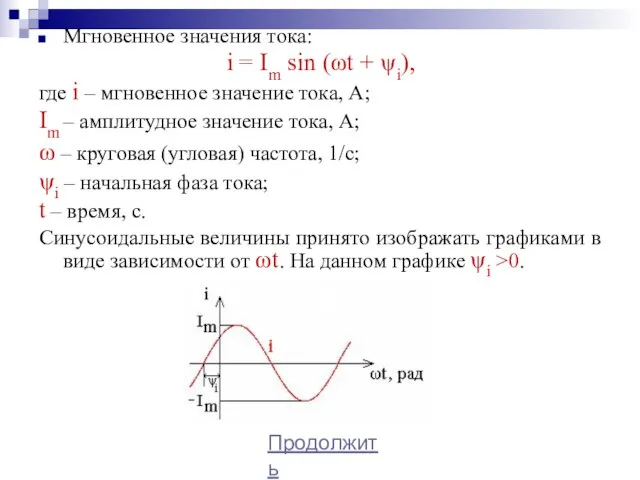
Мгновенное значения тока:
i = Im sin (ωt + ψi),
где i – мгновенное значение тока, А;
Im – амплитудное значение тока, А;
ω – круговая (угловая) частота, 1/с;
ψi – начальная фаза тока;
t – время, с.
Синусоидальные величины принято изображать графиками в виде зависимости от ωt. На данном графике ψi >0.
Продолжить

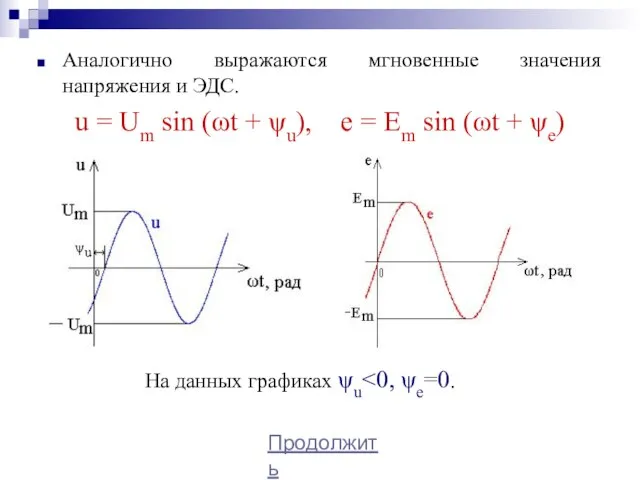
Аналогично выражаются мгновенные значения напряжения и ЭДС.
u = Um sin (ωt + ψu), e = Em sin (ωt + ψe)
Продолжить
На данных графиках ψu<0, ψe=0.

Начальная фаза тока (ЭДС, напряжения) ψi, ψe, ψu – это значение фазы в момент времени t = 0.
Разность начальных фаз двух синусоидальных величин одной и той же частоты называют сдвигом фаз.
Сдвиг фаз между напряжением и током определяется вычитанием начальной фазы тока из начальной фазы напряжения:
φ = ψu – ψi
Продолжить

Действующее значение переменного тока (ЭДС, напряжения) – это среднеквадратичное значение переменного тока (ЭДС, напряжения) за период Т.
Если ток, ЭДС или напряжение изменяются по синусоидальному закону, то действующее значение составляет :
Продолжить

В резистивном элементе происходит преобразование электрической энергии в тепловую.
Если приложено синусоидально изменяющееся напряжение
u = Um sin ωt,
То, по закону Ома, мгновенное значение тока в цепи:
i = u/R = (Um/R) sin ωt = Im sin ωt
Продолжить
Цепь переменного тока с резистивным элементом

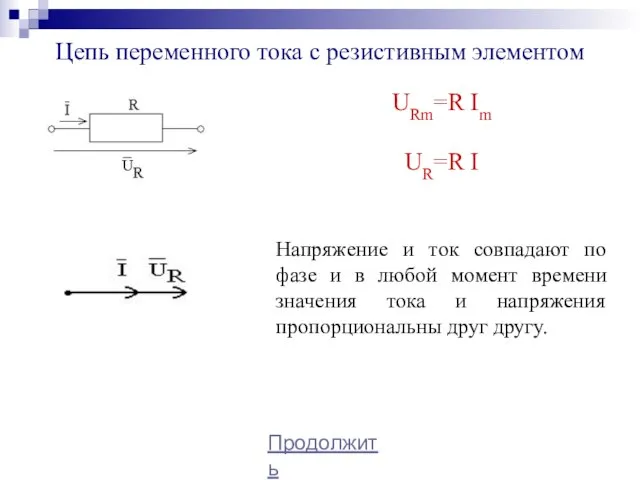
Цепь переменного тока с резистивным элементом
Продолжить
URm=R Im
UR=R I
Напряжение и ток совпадают по фазе и в любой момент времени значения тока и напряжения пропорциональны друг другу.

Цепь переменного тока с индуктивным элементом
Индуктивный элемент создает магнитное поле.
Если ток синусоидальный i = Im sin ωt, то тогда
u = - e = L (d i/d t)= ULm cos ωt = ULm sin (ωt+π/2)
Продолжить
ULm=ωL Im
Величина ХL =ωL – индуктивное сопротивление, Ом.
Напряжение на индуктивном элементе по фазе опережает ток на угол φ= π/2.

Неразветвленная цепь переменного тока
с резистивным и индуктивным элементами
Продолжить

Неразветвленная цепь переменного тока
с резистивным и индуктивным элементами
Напряжение опережает по фазе ток на угол φ:
Действующее значение напряжения U (В):
Полное сопротивление цепи Z (Ом):
Ток в цепи I (A):
Продолжить

Цепь с емкостным элементом
Емкостный элемент создает электрическое поле.
Если в цепи проходит ток i=Imsin(ωt), i=dq/dt=C(duC/dt) , то тогда напряжение
то есть напряжение отстает от тока на угол π/2.
Действующее значение тока в цепи: I=U/XC, где ХС=1/(ωС) – емкостное сопротивление, Ом.
Продолжить

Неразветвленная цепь переменного тока
с резистивным и емкостным элементами
Напряжение на зажимах цепи
Действующее значение напряжения
Разность фаз
Продолжить

Неразветвленная цепь переменного тока
с резистивным, индуктивным и емкостным элементами
Значение напряжения на зажимах этой цепи равно сумме значений трех составляющих:
Действующее значение
Продолжить

Неразветвленная цепь переменного тока
с резистивным, индуктивным и емкостным элементами
Сдвиг фаз между напряжением и током:
Продолжить
Х=XL-XC – реактивное сопротивление

Мощности цепи
Активная мощность, Вт:
P = U I cosφ = URI = I2R
Реактивная мощность, вар:
Q = U I sinφ = (UL – UC)I= I2X
Полная мощность, ВА:
S = U I = I2Z =
Продолжить

Резонанс напряжений
В неразветвленной цепи R-L-C при равенстве реактивных сопротивлений XL=XC наступает резонанс напряжений
Полное сопротивление принимает минимальное значение, равное активному сопротивлению: Z = R.
Падения напряжений UL и UC находятся в противофазе. При резонансе UL=UC равны между собой и приобретают максимальное значение. Ток в цепи имеет наибольшее значение I=U/R и совпадает по фазе с напряжением, то есть φ=0 и коэффициент мощности cos φ=1.
Продолжить

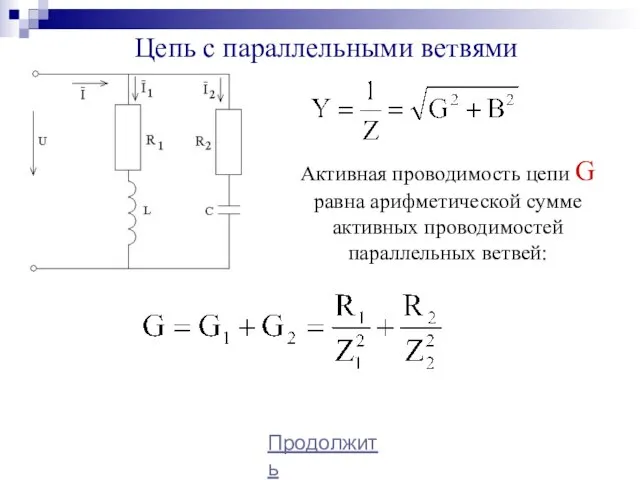
Цепь с параллельными ветвями
Рассмотрим разветвленную цепь, состоящую из двух ветвей.
Ток неразветвленной части цепи может быть определен по закону Ома: I = U/Z = UY, где Y-полная проводимость цепи.
Продолжить

Цепь с параллельными ветвями
Продолжить
Активная проводимость цепи G равна арифметической сумме активных проводимостей параллельных ветвей:

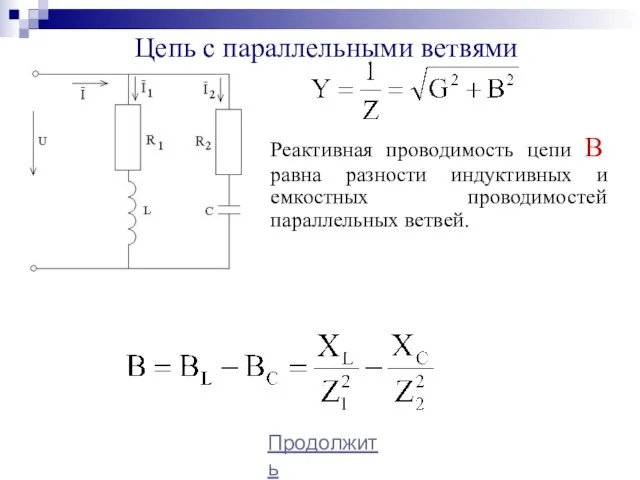
Цепь с параллельными ветвями
Продолжить
Реактивная проводимость цепи B равна разности индуктивных и емкостных проводимостей параллельных ветвей.

Цепь с параллельными ветвями
Продолжить
В цепи можно получить резонанс токов при условии равенства проводимостей BL=BC, тогда полная проводимость цепи Y=G. Угол сдвига фаз φ между током I и напряжением U в неразветвленной части цепи равен нулю, так как реактивные составляющие токов в ветвях Ip1 и Ip2 равны между собой и находятся в противофазе.
Цепь обладает только активной мощностью.

Компенсация реактивной мощности
Продолжить
Идея компенсации реактивной энергии индуктивного потребителя заключается в подключении к нему емкостного потребителя, в результате чего потребление реактивной энергии всей установкой уменьшается.
Схема замещения индуктивного потребителя содержит резистивный и индуктивный элементы с сопротивлениями R и XL, активная мощность Р и напряжение U потребителя заданы.

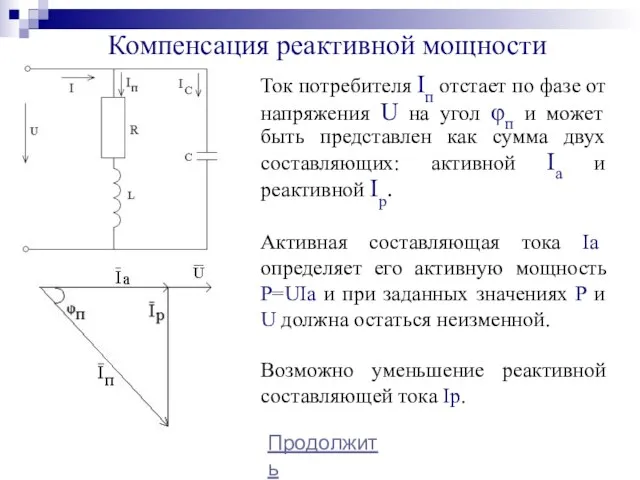
Компенсация реактивной мощности
Продолжить
Ток потребителя Iп отстает по фазе от напряжения U на угол φп и может быть представлен как сумма двух составляющих: активной Ia и реактивной Ip.
Активная составляющая тока Ia определяет его активную мощность Р=UIa и при заданных значениях P и U должна остаться неизменной.
Возможно уменьшение реактивной составляющей тока Iр.

Компенсация реактивной мощности
Продолжить
Необходимо включить параллельно индуктивному потребителю батарею конденсаторов, чтобы повысить коэффициент мощности потребителя cos φп до заданного значения cos φ.

Компенсация реактивной мощности
Продолжить
Ток батареи конденсаторов IC, которая подключается параллельно индуктивному потребителю, должен быть равен разности реактивных составляющих токов потребителя до компенсации Ip и после компенсации Ip1.

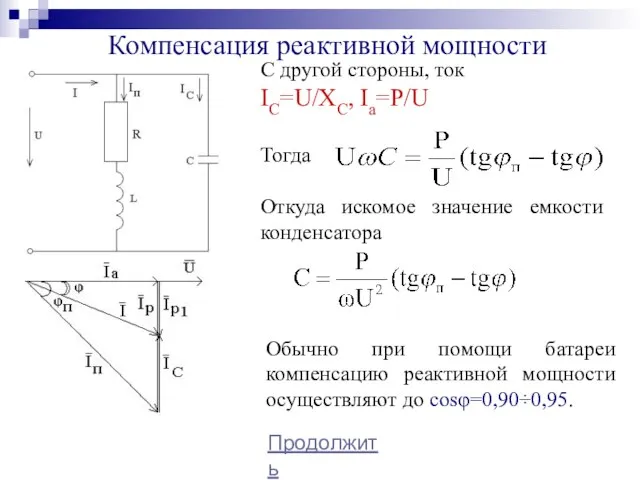
Компенсация реактивной мощности
Продолжить
С другой стороны, ток
IC=U/XC, Ia=P/U
Тогда
Откуда искомое значение емкости конденсатора
Обычно при помощи батареи компенсацию реактивной мощности осуществляют до cosφ=0,90÷0,95.

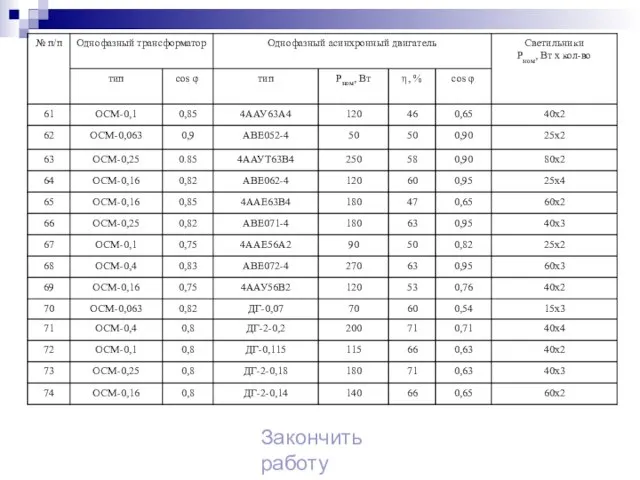
Практическое задание
К однофазной цепи синусоидального тока напряжением Uном=220 В подключены потребители:
однофазный трансформатор ОСМ-0,16, cos φ=0,8;
однофазный асинхронный двигатель ДГ-2-0,14, Рном=140Вт, η=66%, cos φ=0,65;
светильники 60 Вт, 2 штуки.
Составить эквивалентную схему замещения потребителей и определить параметры ее элементов.
Рассчитать емкость батареи конденсаторов, которую нужно подключить к потребителю для снижения реактивной мощности до нуля.
Продолжить

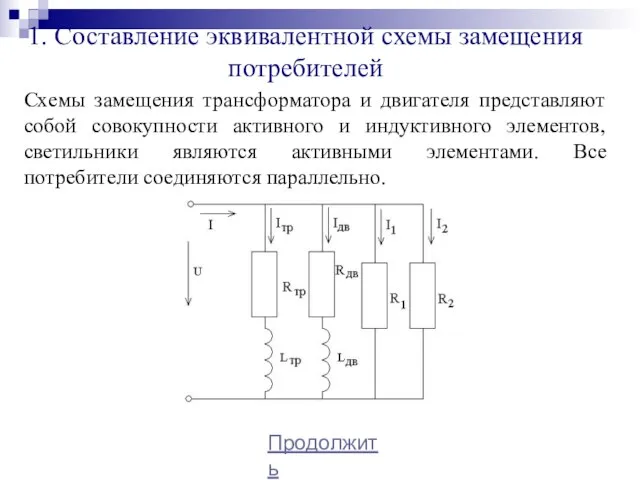
1. Составление эквивалентной схемы замещения потребителей
Схемы замещения трансформатора и двигателя представляют собой совокупности активного и индуктивного элементов, светильники являются активными элементами. Все потребители соединяются параллельно.
Продолжить

Для определения параметров схемы замещения рассматриваем каждую из параллельных ветвей цепи отдельно.
Расчет трансформатора:
Число 0,16 в маркировке трансформатора означает его полную мощность, выраженную в киловольтамперах, то есть:
Sтр=0,16 кВА =160 ВA Pтр=Sтрcosφтр=128 Вт
ток Iтр=Sтр/U=160/220=0,727 A
сопротивления: Zтр=U/Iтр=220/0,727=302,613 Ом
Rтр=Pтр/Iтр2=128/0,7272=242,182 Ом
Продолжить
индуктивность Lтр=ХL/2πf=0,578 Гн

Расчет двигателя:
Сначала необходимо определить активную мощность, потребляемую двигателем из сети:
Рдв=Рном/ηдв=140/0,66=212,121 Вт
полная мощность Sдв=Pдв/cosφдв=212,121/0,65=326,34 BA
ток Iдв=Sдв/U=326,34/220=1,483 A
сопротивления:
Zдв=U/Iдв=220/1,483=148,348 Ом
Rдв=Pдв/Iдв2=212,121/1,4832=96,45 Ом
Продолжить
индуктивность Lдв=ХLдв/2πf=0,359 Гн

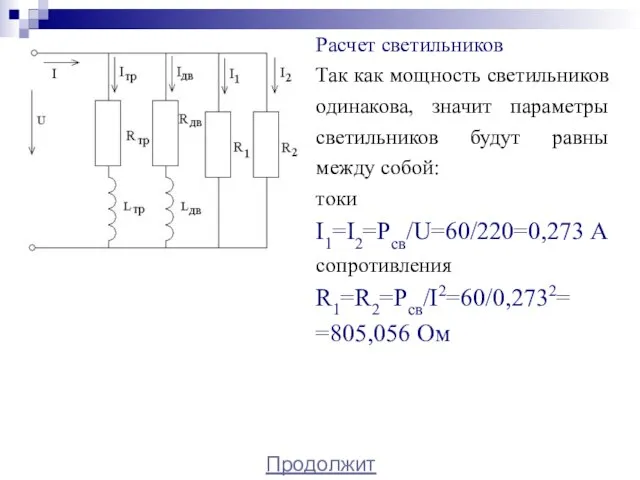
Расчет светильников
Так как мощность светильников одинакова, значит параметры светильников будут равны между собой:
токи
I1=I2=Pсв/U=60/220=0,273 А
сопротивления
R1=R2=Pсв/I2=60/0,2732=
=805,056 Ом
Продолжить

Свернем данную схему в ей эквивалентную методом активно-реактивных проводимостей
Определяем проводимости:
активные:
Gтр=Rтр/Zтр2=242,182/302,6132=0,002644 См
Gдв=Rдв/Zдв2=96,45/148,3482= 0,004383 См
G1=G2=1/R1=1/R2=1/805,056=0,001242 См
Эквивалентная активная проводимость цепи:
G=Gтр+Gдв+G1+G2=0,009511 См
Продолжить

Определяем проводимости:
реактивные:
Bтр=XLтр/Zтр2=181,446/302,6132=0,001981 См
Bдв=XLдв/Zдв2=112,714/148,3482= 0,005122 См
B1=B2=0
Эквивалентная реактивная проводимость цепи: B=Bтр+Bдв=0,007103 См
Эквивалентная полная проводимость
Продолжить

Определяем эквивалентные сопротивления всей цепи, индуктивность, ток и активную мощность:
Zэкв=1/Y=1/0,0119=84,0336 Ом
Rэкв=G/Y2=67,1633 Ом
XLэкв=B/Y2=50,1589 Ом
Lэкв=XLэкв/2πf=0,1597 Гн
Iэкв=U/Zэкв=2,618 А
Р=RэквIэкв2=460,3322 Вт
Продолжить

Определяем:
tg φп=tg φэкв=XLэкв/Rэкв=
=59,7845/69,5985=0,859
По условию задачи
tg φ=0.
Продолжить
2. Подключаем блок конденсаторов для снижения реактивной мощности

Параметры диаграммы:
Iэкв=2,618 А IC=U/XC=U·2πfC=1,5626 A
φп=φэкв=arctg(XLэкв/Rэкв)=arctg 0,859=40,66° φ=0
Масштаб выбираем произвольно, например 1см = 0,5 А
Продолжить
Построим векторную диаграмму токов
(повторить сложение векторов)
Таким образом, при полной компенсации реактивной мощности
I=Iэкв cos φпр=
=2,09 A

Iэкв=2,618 А
φп=40,66°
Продолжить
Покажем построение графиков мгновенных значений тока и напряжения для эквивалентной схемы
Мгновенные значения токов и напряжения определяются:
i = Im sin (ωt + ψi)
u = Um sin (ωt + ψu)
φп= ψu – ψi=40,66°
Примем ψu=0, тогда ψi=-40,66°=
=-(40,66°/180°)π =-0,226π радиан

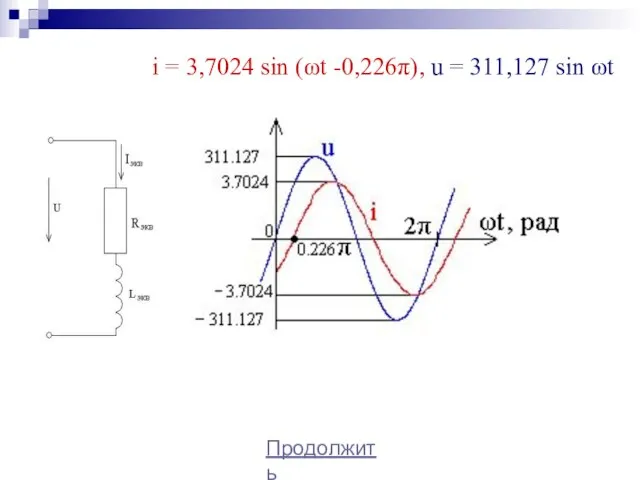
Продолжить
i = 3,7024 sin (ωt -0,226π), u = 311,127 sin ωt

IС=1,5626 А
φС= - 90°
Продолжить
Покажем построение графиков мгновенных значений для емкостного элемента
Мгновенные значения токов и напряжения определяются:
i = Im sin (ωt + ψi)
u = Um sin (ωt + ψu)
Примем ψu=0, тогда
ψi= 90°= π/2 радиан

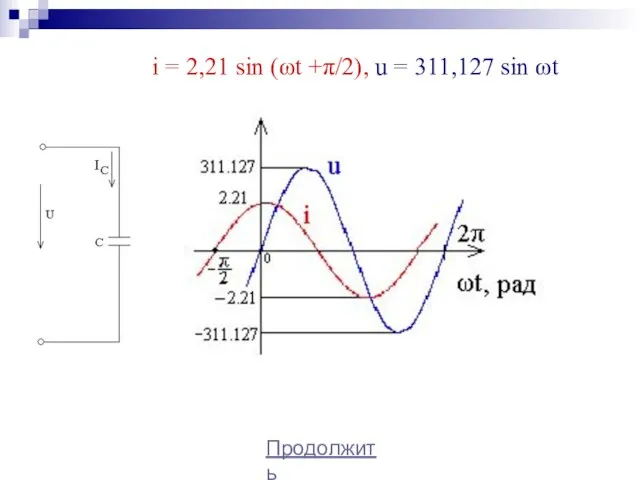
Продолжить
i = 2,21 sin (ωt +π/2), u = 311,127 sin ωt

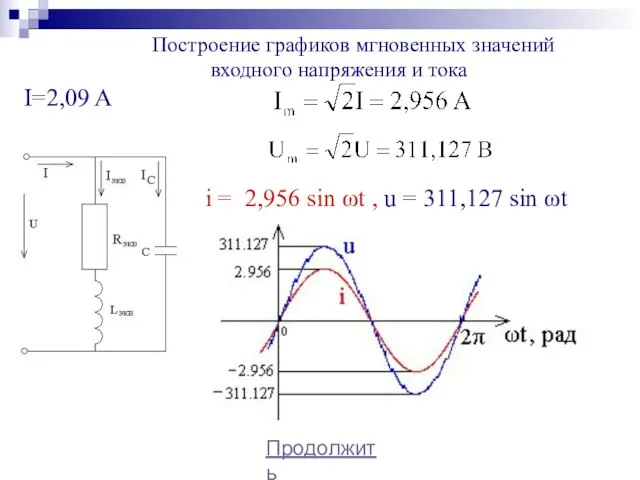
Продолжить
i = 2,956 sin ωt , u = 311,127 sin ωt
Построение графиков мгновенных значений входного напряжения и тока
I=2,09 A

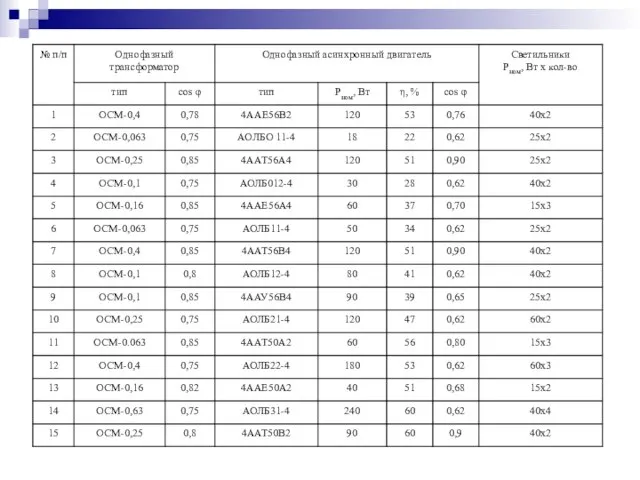
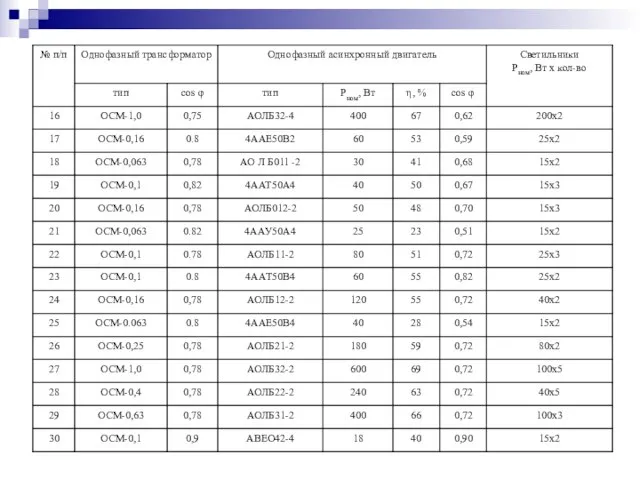
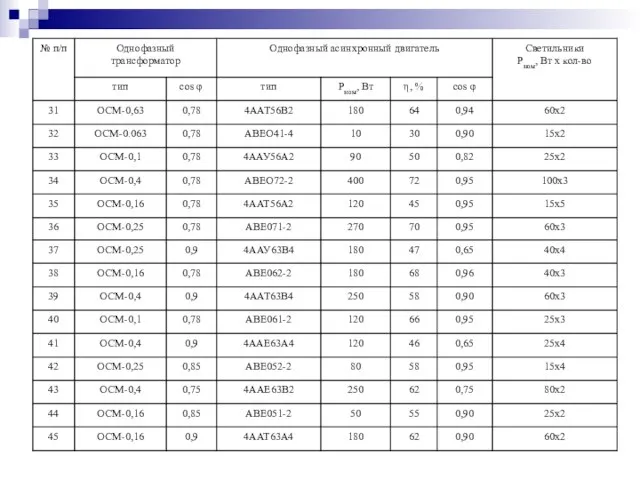
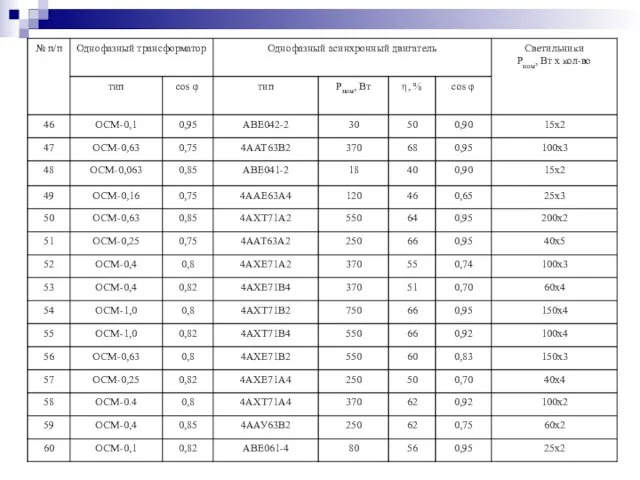
Задачи для самостоятельного решения
К однофазной цепи синусоидального тока напряжением Uн=220 В подключены потребители, типы и характеристики которых приведены в таблице.
Для светильников cos φ=1.
Составить эквивалентную схему замещения потребителей и определить параметры ее элементов.
Рассчитать емкость батареи конденсаторов, которую нужно подключить к потребителю для снижения реактивной мощности до нуля.

Закончить работу

Векторы
Вектор – направленный отрезок, имеет определенную длину, направление указывает стрелка.
Вектор
Вектор
Отрезок AB
Продолжить

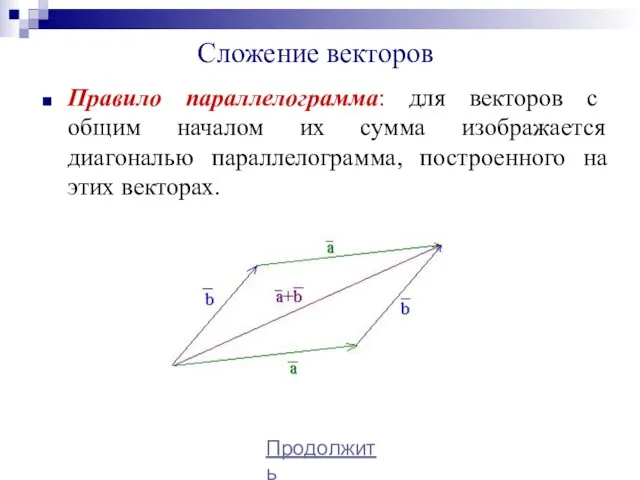
Сложение векторов
Правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
Продолжить

В нашем случае откладываем в качестве основного вектор напряжения цепи.
Строим векторы тока в произвольно выбранном масштабе: ток IC на конденсаторе опережает напряжение на угол 90°, ток Iэкв отстает на угол 40,66° (положительное направление угла – против часовой стрелки):
Продолжить

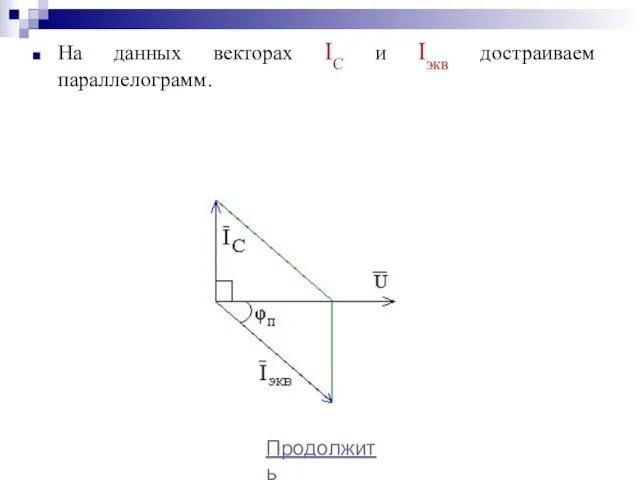
На данных векторах IС и Iэкв достраиваем параллелограмм.
Продолжить