Окружающий нас мир полон движущихся объектов. Их движение, в широком смысле, можно разделить на два класса в зависимости от того, ос

Введение
Окружающий нас мир полон движущихся объектов. Их движение, в широком смысле, можно разделить на два класса в зависимости от того, остается ли объект вблизи некоторого среднего положения или такого положения нет. Примерами движений первого класса являются колебания маятника, вибрация струны скрипки, колебания уровня воды в чашке, движение электронов в атомах, свет, многократно отражающийся от зеркал лазера. В качестве примеров движений второго класса можно указать на скольжение хоккейной шайбы, движение импульса по длинному тросу при дергании за конец троса, волны океана, катящиеся к берегу, пучок электронов в телевизионной трубке, луч света, испущенный звездой и принятый нашим глазом. Иногда одно и то же движение можно отнести
к любому из этих классов в зависимости от точки зрения на явление: так, волны океана движутся к берегу, но вода (и утка, сидящая на поверхности) совершает движение вверх и вниз, а также вперед и назад относительно некоторого среднего положения. Точно
так же импульс смещения бежит по канату, но вещество каната колеблется относительно среднего положения.

Свободные
Вынужденные
Автоколебания
Колебания

Гармонические колебания
Изменения состояния движения, обладающие той или иной степенью повторяемости, называются колебаниями.
Колебания, при которых состояние движения тела точно повторяется через равные промежутки времени, называются периодическими.
Из всех периодических движений важное место в физике и
технике занимают колебания, т. е. такие движения, при которых
материальная точка перемещается взад и вперед по отрезку
прямой (или кривой) между крайними его точками (рис. 1).
В зависимости от характера движения точки на отрезке колебания делятся на гармонические и негармонические. Гармоническими называют колебания, при которых дуговая координата движущейся точки изменяется во времени по синусоидальному или по косинусоидальному закону (рис. 1):
s=s0sin(ωt+φ),
s=s0cos(ωt+φ).
Для гармонических колебаний график изменения дуговой координаты во времени имеет синусоиды или косинусоиды (рис. 2,а).
Все колебания, при которых дуговая координата изменяется по иному закону, будут негармоническими. На рисунках 2, б, в показаны графики s(t) для видов негармонических колебаний.
Среди других видов колебаний гармонические занимают особое положение. Это обусловлено тем, что, как показал Фурье, любое периодическое движение (любое колебание) можно рассматривать как результат сложения конечного или бесконечного числа простых гармонических колебательных движений. Таким образом, гармоническое колебание представляет собой простейший вид колебательного движения, к которому может быть сведено любое сколь угодно сложное колебание.
Учение о гармонических колебаниях составляет основу более общего учения о колебаниях вообще.

Амплитуда колебаний (А или S0)
Важной характеристикой колебательного движения является амплитуда.
Амплитудой гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия.
Амплитуда может иметь различные значения в зависимости от того, насколько мы смещаем тело от положения равновесия в начальный момент времени, и от того, какая скорость сообщается этом телу. Амплитуда определяется начальными условиями. Но максимальные значения модуля синуса и косинуса равны единице. Поэтому решение уравнения s=Аsin(ωt+φ), не может выражаться просто синусом или синусом. Оно должно иметь вид произведения амплитуды А на синус или косинус.
Фаза колебаний или фазовая постоянная (φ)
Величина φ, стоящую под знаком косинуса или синуса.
Фаза колебаний характеризует положение точки на окружности в данный момент времени. Например, положение В (рис. 1) колеблющаяся точка проходит дважды: первый раз – двигаясь в прямом и второй раз – двигаясь в обратном направлении. Хотя смещение S в обоих случаях одинаково, но фазы будут разными, иль направления движения не совпадают. Фаза выражается в радианах (рад). Угол φ0 характеризует положение точки в момент, соответствующий началу отсчета времени (t=0), почему его и называют начальной фазой. Угол φ0 может быть как положительным, так и отрицательным. Часто значение фазы нас не интересует, и мы можем всегда «перевести часы» так, чтобы φ стало равным нулю. Тогда вместо более общего уравнения s=s0sin(ωt+φ) имеем s=s0sinωt или s=s0cosωt.
Период (Т)
Минимальный промежуток времени Т, через который движение тела полностью повторяется.
Частота (ν)
Величина ν= 1/Т обозначает число колебаний за одну секунду. Эту величину называют частотой гармонических колебаний (иногда ее называют линейной частотой). Частоту ν измеряют в герцах (Гц). За 1 Гц принимают частоту такого колебания, при котором колеблющаяся точка за 1 совершает одно колебание: 1 Гц = 1 с-1.
Угловая или циклическая частота (ω)
Постоянная для данного колебания величина. Измеряется в рад/сек. Выражается через частоту колебаний так: ω = 2πυ.
Смещение (S или X)
Дуговая координата , характеризующая положение точки на траектории в момент времени t (смещение колеблющейся точки от среднего положения).
Кинематика гармонических колебаний
Физические величины, характеризующие гармоническое колебание

Если траектория колеблющейся точки представляет собой отрезок прямой, то колебания называют прямолинейными (или, что не совсем правильно, просто линейными). Направляя ось x вдоль этого отрезка и выбирая в качестве начала отсчета координаты х среднее положение колеблющейся точки, можно закон движения при гармоническом колебании записать так:
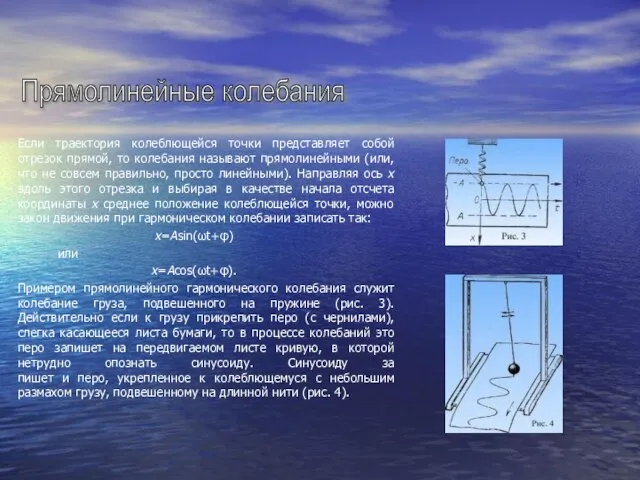
x=Asin(ωt+φ)
или
x=Acos(ωt+φ).
Примером прямолинейного гармонического колебания служит колебание груза, подвешенного на пружине (рис. 3). Действительно если к грузу прикрепить перо (с чернилами), слегка касающееся листа бумаги, то в процессе колебаний это перо запишет на передвигаемом листе кривую, в которой нетрудно опознать синусоиду. Синусоиду за
пишет и перо, укрепленное к колеблющемуся с небольшим размахом грузу, подвешенному на длинной нити (рис. 4).
Прямолинейные колебания

Если траектория колеблющейся точки есть часть окружности радиуса R, то смещение s (рис. 5) и амплитуду s0 можно выразить через радиус окружности R и угол отклонения α радиус-вектора R:
s=Rα, s0=Rα
Тогда закон движения запишется через угловые величины следующим образом:
α = α0sin(ωt+φ)
или
α = α0cos(ωt+φ).
где α0 - угол наибольшего отклонения радиус-вектора R.
Колебания, совершаемые по дуге окружности

Пусть твердое тело имеет неподвижную ось и вращается около нее
попеременно, то в одну, то в другую сторону. Такой вид движения называют крутильными колебаниями. Каждая точка тела при этом совершает колебания по дуге окружности соответствующего радиуса. Если эти колебания точек гармонические, то движение их будет описываться с помощью угловых величин одним и тем же для всех точек уравнением, которое, таким образом, будет являться уравнением гармонических крутильных колебаний тела в целом. В этом случае α0 есть амплитуда; (ω —круговая частота; ωt+φ — фаза крутильных колебаний. Под α (и α0) следует понимать поворот некоторой плоскости, связанной с телом, относительно другой плоскости, фиксированной в пространстве.
Примером крутильных колебаний служит движение маятника наручных часов. К крутильным относятся колебания твердого тела, имеющего точку подвеса, не совпадающую с центром тяжести тела. Если отклонить это тело, а затем предоставить самому себе, оно начнет колебаться. При этом каждая его точка движется по дуге соответствующей окружности. Как будет показано ниже, колебания в этом случае можно считать гармоническими только при малых амплитудах.
Крутильные колебания

Пусть изменение смещения колеблющейся точки происходит синусоидальному
закону:
x=Asin(ωt+φ)
Производная от этой функции выражает скорость точки:
υ = dx/dt = Aωcos(ωt+φ) = υ0cos(ωt+φ),
где υ0 = Aω — амплитуда скорости.
Из соотношений видно, что в те моменты времени, когда смещение точки равно нулю (синус равен нулю), скорость будет наибольшей (косинус равен единице) и, наоборот, в моменты времени, в которые смещение максимально, скорость обращается в нуль. Другими словами, скорость имеет наибольшее значение, когда точка проходит положение равновесия, и она обращается в
нуль, когда точка достигает наибольшего отклонения. Это хорошо видно на примере колебаний математического маятника: маятник на мгновение останавливается в момент наибольшего отклонения: наибольшую скорость он имеет, когда проходит положение равновесия. Формулу υ = υ0cos(ωt+φ) можно записать так:
υ = υ0sin(ωt+φ+π)
Отсюда видно, что скорость υ опережает по фазе смещение х на π/2, т. е. на четверть периода.
Если продифференцируем по времени выражение υ = υ0cos(ωt+φ), то найдем закон изменения ускорения:
α = dυ/dt = -Aω2sin(ωt+φ) = -α0sin(ωt+φ),
где α0 = Aω2 =υ0 ω — амплитуда ускорения.
Сопоставляя формулу α = -α0sin(ωt+φ), с выражением x=Asin(ωt+φ) для смещения, мы приходим к выводу, что ускорение и смещение одновременно обращаются в нуль и одновременно достигают наибольших значений.
Выражение α = -α0sin(ωt+φ) можно записать и в таком виде:
α = Aω2sin(ωt+φ+ π)
Сравнивая эту формулу с x=Asin(ωt+φ) , легко убедиться в том, что ускорение опережает по фазе смещение на π или на 1/2 периода. Для краткости говорят: ускорение и смещение изменяются в противофазе. Это означает, что в тот момент, когда одна из этих величин достигает максимального значения (положительного амплитудного значения), другая достигает минимального значения (отрицательного амплитудного значения).
Поскольку x=Asin(ωt+φ) , то α = -α0sin(ωt+φ) можно записать так:
α = - ω2x
Это значит, что ускорение при гармоническом колебании пропорционально смещению и направлено к одной и той же точке — среднему положению. Из рисунка 6 видно, что если х положительно, то а отрицательно, т. е. направлено к точке О, если же х отрицательно, то а положительно, т. е. опять направлено к точке О.
Рассуждая подобным образом, можно получить, что угловая скорость и угловое ускорение при крутильных колебаниях вида
α = α0sin(ωt+φ)
будут равны:
dα/dt = Ω = α0cos(ωt+φ),
dΩ/dt = β = -α0 ω2sin(ωt+φ) = - ω2 α.
Скорость и ускорение точки при гармоническом колебании

Пусть радиус-вектор ОС (рис. 7) равномерно вращается около центра О с угловой скоростью ω. Через О проведем ось х рассмотрим проекцию вектора ОС на эту ось. Она равна:
X=lOClcosα
Здесь угол α непрерывно изменяется:
α = ωt+φ
где φ — угол между вектором ОС и осью х в момент времени t=0. Если обозначить модуль вектора ОС через A, то X=lOClcosα
запишется так:
x=Asin(ωt+φ)
Полученное выражение показывает, что гармоническое колебание можно рассматривать как проекцию вращающегося вектора, причем циклическая частота колебания равна угловой скорости вращения вектора, а амплитуда
колебания — модулю вектора.
Очевидно, что одному обороту вектора ОС соответствует одно колебание. Так как угловую скорость вращения можно выразить через число оборотов в секунду n
ω = 2πn
то и циклическую частоту можно выразить через число колебаний в секунду
ω = 2πν
Связь гармонического колебания с вращением
радиус-вектора

Одна и та же точка может одновременно участвовать в двух (и более) движениях. Примером служит падение шарика, бро­шенного горизонтально. В этом случае можно рассматривать, что шарик совершает два взаимно перпендикулярных прямоли­нейных движения: равномерное по горизонтали и равнопере­менное по вертикали. Одна и та же точка может участвовать в двух (и более) движениях колебательного вида. Например, подвешенный на длинной нити шарик можно поочередно за­ставить колебаться то в одной вертикальной плоскости, то в другой, перпендикулярной первой. Но можно заставить его колебаться одновременно в двух этих плоскостях. Для этого шарик, колеблющийся в одной плоскости, надо ударить молотком в на­правлении, перпендикулярном этой плоскости. Два колебания во взаимно перпендикулярных плоскостях «сложатся» и перед наблюдающим предстанет результирующее движение, которое в данном случае представляет собой движение шарика по эллипсу в горизонтальной плоскости.
Мы рассмотрим два случая сложения двух колебаний:
а) когда оба колебания совершаются по одной прямой и
б) когда они совершаются по взаимно перпендикулярным направлениям.
Результирующее смещение тела, участвующего в нескольких колебательных движениях, получается как геометрическая сумма независимых смещений, которые тело приобретает, участвуя в каждом из слагающих колебаний.
Сложение колебаний

Сложение двух колебаний одинаковой частоты
Положим, тело участвует одновременно в двух гармонических колебательных движениях, происходящих в одном направлении с одинаковой частотой, но с различными начальными фазами и амплитудами:
x1=а1cos(ωt+φ01)
x2=а2cos(ωt+φ02)
Построим векторные диаграммы этих колебаний (рис. 8). Результирующее смещение x тела, участвующего одновременно в обоих колебаниях, равно сумме проекций x1 и x2 на ось x векторов а1 и а2, или, что то же, проекции вектора а=а1+ а2.
Так как векторы а1 и а2 вращаются с одинаковой угловой скоростью ω, то сдвиг фаз (угол φ02- φ01) между ними остается постоянным. Изображенный на рисунке 8 треугольник вращается как жесткий, его стороны вращаются с той же угловой скоростью, что и векторы а1 и а2.
Очевидно, уравнение результирующего колебания будет:
x=x1+ x2=а cos(ωt+φ0),
где
а2=а21+а22+2а1а2cos(φ02- φ01),
а начальная фаза φ0 определяется соотношением:
tg φ0 = (a1sin φ01 + a2sin φ02)/(a1cos φ01 + a2cos φ02)
Таким образом, тело, участвуя в двух гармонических колебаниях, происходящих в одном направлении с одинаковой частотой, совершает гармоническое колебание в том же направлении и с той же частотой, что и составляющие колебания.
При этом величина амплитуды результирующего колебания зависит от сдвига фаз φ02- φ01 составляющих колебаний. Если сдвиг фаз между составляющими колебаниями равен нулю или 2πn, где n – целое число, то
а2=а21+а22+2а1а2 = (а1 + а2)2,
откуда
а = а1 + а2
т. е. при сдвиге фаз φ02- φ01 = 2πn, где n=0, 1, 2, 3, ... , амплитуда результирующего колебания равна сумме амплитуд составляющих колебаний.
Если а1=а2, то амплитуда результирующего колебания а=2а1 =2а2, т. е. амплитуда в результате сложения колебаний удваивается. Так как энергия колебаний пропорциональна квадрату амплитуды, то в этом случае происходит увеличение энергии в четыре раза.
Если сдвиг фаз равен нечетному числу π, т. е. φ02- φ01 =(2n+1) π, где n=0, 1, 2, 3, ... , то
а2=а21+а22 - 2а1а2 = (а1 - а2)2,
или
а=\а2—а1\,
так как по смыслу а>0.
Сложение колебаний одного направления

При разности фаз φ02- φ01 =(2n+1) π, где n=0, 1, 2, ... , амплитуда результирующего колебания равна модулю разности амплитуд составляющих колебаний. Колебания ослабляют друг друга.
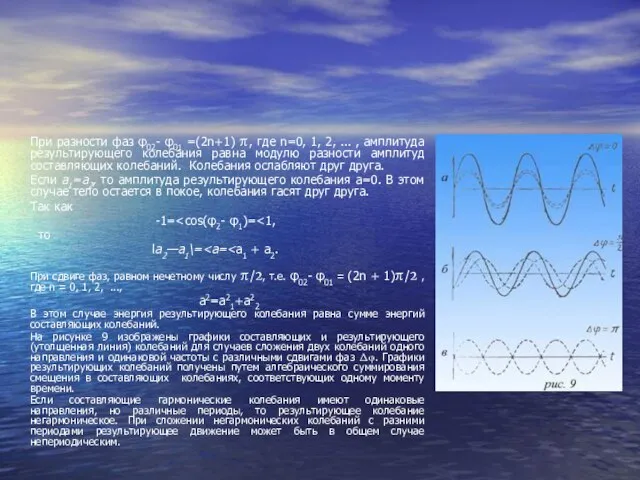
Если а1=а2, то амплитуда результирующего колебания а=0. В этом случае тело остается в покое, колебания гасят друг друга.
Так как
-1=
то
lа2—а1\=
При сдвиге фаз, равном нечетному числу π/2, т.е. φ02- φ01 = (2n + 1)π/2 , где n = 0, 1, 2, ...,
а2=а21+а22
В этом случае энергия результирующего колебания равна сумме энергий составляющих колебаний.
На рисунке 9 изображены графики составляющих и результирующего (утолщенная линия) колебаний для случаев сложения двух колебаний одного направления и одинаковой частоты с различными сдвигами фаз Δφ. Графики результирующих колебаний получены путем алгебраического суммирования смещения в составляющих колебаниях, соответствующих одному моменту времени.
Если составляющие гармонические колебания имеют одинаковые направления, но различные периоды, то результирующее колебание негармоническое. При сложении негармонических колебаний с разними периодами результирующее движение может быть в общем случае непериодическим.

Сложение двух колебаний разной частоты
Рассмотрим случай сложения двух гармонических колебаний одного направления, но разного периода.
Построим на диаграмме векторы а1 и а2 для начального момента времени (рис. 10) и для момента времени t. Как можно видеть из чертежа, угол между векторами а1 и а2 со временем меняется, так как угловые скорости вращения векторов различны. Значит, амплитуда результирующего колебания меняется со временем. Угловая скорость ее вращения непостоянная, и, следовательно, колебание происходит по закону, отличному от гармонического.
Пусть амплитуды колебаний одинаковы и начальные фазы равны:
а1=а2=а0 и φ01= φ02 = φ0
Тогда
x= а0 cos(ω1t+φ0) + а0 cos(ω2t+φ0),
откуда
х = 2а0 cos((ω2 – ω1)t/2)cos((ω2 – ω1)t/2 + φ)
Амплитуда результирующего колебания периодически изменяется но абсолютной величине. Период ее изменения:
Ta = 2π/((ω2 – ω1)/2).
Период изменения смещения:
T = 2π/((ω2 + ω1)/2).
Очевидно, Та>Т.

Биения
Если частота ω2 мало отличается от ω1 то возникает явление биений. Чтобы представить себе процесс возникновения биений, положим, что два колебания равной амплитуды и почти одной частоты в начальный момент совпадают по фазе. В этот момент колебания происходят с удвоенной амплитудой. Затем фазы колебаний медленно расходятся, и через некоторое время сдвиг фаз между колебаниями достигает величины π. В этот момент колебания гасят друг друга и амплитуда результирующего колебания равна нулю. Продолжая расти, сдвиг фаз достигает 2π и амплитуда результирующего колебания опять оказывается равной удвоенной амплитуде составляющих колебаний. На рисунке 11 изображено возникновение биений, т. е. периодического изменения амплитуды при сложении двух колебаний близкой частоты. Если амплитуды составляющих колебаний не равны, то амплитуда результирующего колебания не спадает до нуля, а проходит при сдвиге фаз π. через минимум.
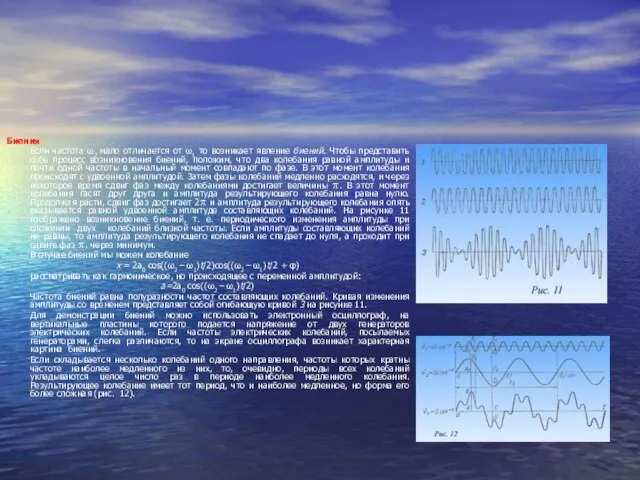
В случае биений мы можем колебание
х = 2а0 cos((ω2 – ω1)t/2)cos((ω2 – ω1)t/2 + φ)
рассматривать как гармоническое, но происходящее с переменной амплитудой:
a=2а0 cos((ω2 – ω1)t/2)
Частота биений равна полуразности частот составляющих колебаний. Кривая изменения амплитуды со временем представляет собой огибающую кривой 3 на рисунке 11.
Для демонстрации биений можно использовать электронный осциллограф, на вертикальные пластины которого подается напряжение от двух генераторов электрических колебаний. Если частоты электрических колебаний, посылаемых генераторами, слегка различаются, то на экране осциллографа возникает характерная картина биений.
Если складывается несколько колебаний одного направления, частоты которых кратны частоте наиболее медленного из них, то, очевидно, периоды всех колебаний укладываются целое число раз в периоде наиболее медленного колебания. Результирующее колебание имеет тот период, что и наиболее медленное, но форма его более сложная (рис. 12).

Для колебаний одинаковой частоты
Рассмотрим движение точки, участвующей одновременно в двух колебаниях, направления которых взаимно перпендикулярны. Этот случай колебаний можно наблюдать на электронном осциллографе, если, создав переменное напряжение от одного генератора электрических колебаний на вертикальных пластинах, отключим генератор развертки с горизонтальных пластин (что возможно в подавляющем большинстве современных осциллографов) и подадим па них напряжение со второго генератора электрических колебаний. Пока генераторы не включены, электронный луч проходит по оси отклоняющих пластин и создает светящуюся точку в центре экрана. В этой точке мы поместим начало координат, а за оси возьмем горизонтальный (ось х) и вертикальный (ось у) диаметры (рис. 13). Включим генератор, соединенный с горизонтальными пластинами. Частота колебаний напряжения этого генератора ω. Светящаяся точка смещается по горизонтальной оси, совершая колебания по гармоническому закону:
x=а1 cos ωt.
Подключая генератор, дающий ту же частоту колебаний, к вертикальным пластинам при отключенных горизонтальных пластинах, мы заставим светящуюся точку смещаться по экрану в вертикальном направлении по закону:
y=a2 cos ωt.
Эти уравнения и представляют собой в сущности кинематические уравнения движения точки. Если мы из них исключим время, то получим уравнение траектории, по которой движется светящаяся точка, участвуя одновременно в двух взаимно перпендикулярных колебаниях:
x/y = a1/a2,
или
x=ya1/a2,
т. е. светящаяся точка движется по прямой, проходящей через положение равновесия (начало координат) и составляющей с осью х угол, тангенс которого определяется соотношением:
tg α =a1/a2
Результирующее смещение, отсчитанное вдоль этой прямой:
s = (x2 + y2)1/2 =(a21 + a22)1/2cos ωt = acos ωt
Длина отрезка, пробегаемого точкой, равна удвоенной амплитуде результирующего колебания:
2a = 2(a21 + a22)1/2.
Таким образом, точка, участвующая одновременно в двух взаимно перпендикулярных колебаниях одной частоты при сдвиге фаз между ними, равном нулю, совершает гармоническое колебательное движение вдоль отрезка прямой, который служит диагональю прямоугольника, образованного отрезками прямых x=±at и у = ±а2, отсекающих на осях х и у отрезки длиной 2a1 и 2a2.
Нетрудно показать, что при сдвиге фаз составляющих колебаний на я колебание светящейся точки происходит по другой диагонали прямоугольника.
Сложение взаимно перпендикулярных колебаний

Рассмотрим случай, когда составляющие колебания сдвинуты по фазе на π/2. Для определенности положим, что колебание вдоль оси х опережает по фазе колебание по оси у и отсчет времени производится от момента, когда светящаяся точка находится в начале координат:
х=a sin ωt.
Тогда в момент возникновения колебаний по оси х вдоль оси у смещения отсутствуют. Светящаяся точка получает смещение, равное а1, т. е. совершает четверть колебания и оказывается в крайнем правом положении, после этого она участвует уже в двух движениях, возвращаясь к положению равновесия по
оси х и отклоняясь по оси у вверх. Колебания происходят по закону:
x= а sin(ωt+ π/2) = a cos ωt,
y =a sin ω
Траектория светящейся точки в этом случае окружность
x2 + y2 = a2,
которую точка обходит против часовой стрелки. Если сдвиг фаз равен 3π/2, то траектория также окружность, но точка обегает ее по часовой стрелке. (Точка начинает двигаться вверх, находясь в край-ном левом положении.) Если амплитуды колебаний x= а sin(ωt+ π/2) = a cos ωt, y =a sin ω не равны, то легко видеть, что точка движется по эллипсу:
x/a1 = cos ωt. y/a2 = sin ωt.
Исключая время, получим:
x2/a21 + y2/a22 = 1,
т. е. уравнение эллипса с осями, совпадающими по направлению с направлением составляющих колебаний. Полуоси эллипса равны а1 и а2 (рис. 14). Движение точки, участвующей в двух взаимно перпендикулярных колебаниях равной частоты с разными мплитудами и сдвигом фаз в π/2, происходит по эллипсу полуосями а1 и а2, лежащими на направлениях составляющих колебаний. Эллипс вписан в прямоугольник, образованный отрезками прямых x=±at и у = ±а2.
То же наблюдается при сдвиге фаз, равном 3π/2, но точка обегает эллипс в этом случае в противоположном направлении.

Для колебаний разной частоты
Если отношение амплитуд меняется, то эллипс деформируется, не меняя своего положения относительно направлений составляющих колебаний. Если меняется сдвиг фаз, то эллипс одновременно и деформируется и меняет свою ориентацию относительно указанных направлений (рис. 15, а). Если периоды составляющих взаимно перпендикулярных колебаний различаются на малую величину, то сдвиг фаз плавно меняется, принимая последовательно все возможные значения, и эллипс постепенно поворачивается и деформируется. Однако и при этом он остается вписанным в прямоугольник со сторонами 2а1 и 2а2.
Изменим частоту одного из генераторов заметным образом. Тогда колебания светящейся точки будут по-прежнему происходить во взаимно перпендикулярных направлениях, но сдвиг фаз будет сильно меняться в пределах одного периода, и мы получим сложную запутанную картину движения точки. Прямоугольник, в котором поворачивался эллипс, окажется сплошь заполненным траекториями светящейся точки.
Картина упрощается, если частоты (периоды) взаимно перпендикулярных колебаний кратны друг другу.
Пусть ω1 = 2 ω2 (рис. 15, б). По истечении одного периода колебания Т2 в направлении оси у точка должна вернуться в начальное положение, так как Т2 равно двум целым периодам колебания Т1 , вдоль оси х. Поэтому траектория точки должна быть замкнутой кривой. Вместе с тем точка за время Т2 два раза достигает крайних положений +а1 и —а1 и один раз —а2 и +а2. Следовательно, она один раз коснется сторон прямоугольника, отстоящих от оси х на расстоянии а2, и дважды сторон, отстоящих от оси у на расстоянии а1.
Вид траекторий зависит от фаз составляющих колебаний, а число точек касания определяется отношением частот. Эти траектории называют фигурами Лиссажу, по имени французского ученого, их впервые наблюдавшего.
На рисунке15 изображены фигуры Лиссажу для разного соотношения частот и разных сдвигов фаз.

Над данным проектом работал Васильев Дмитрий, ученик школы №26, города Йошкар-Олы, республики Марий Эл.
E-mail:
[email protected]