OpenMP

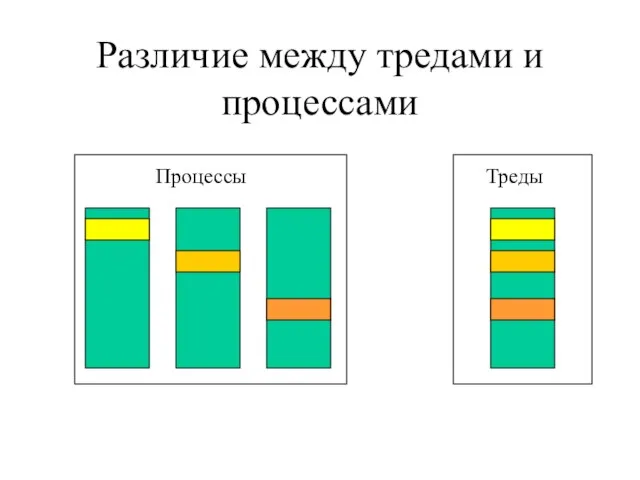
Различие между тредами и
процессами
Процессы
Треды

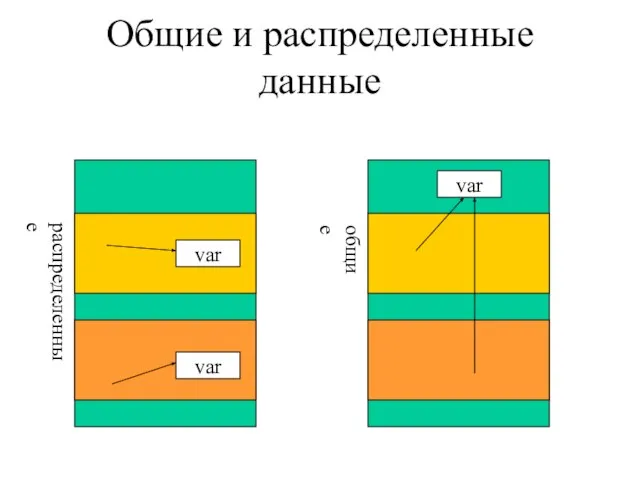
Общие и распределенные данные
var
var
var
распределенные
общие

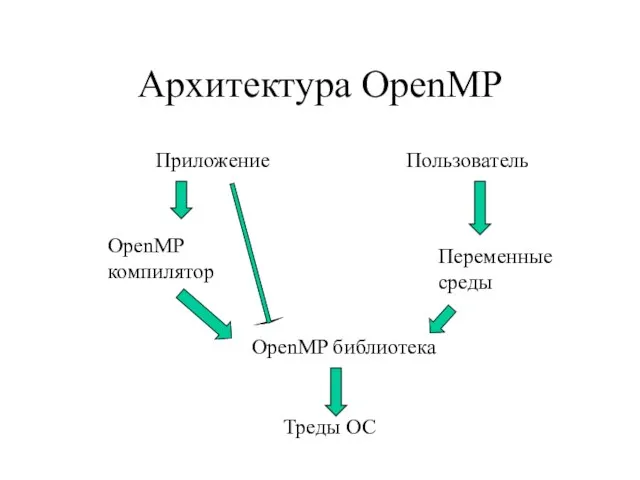
Архитектура OpenMP
Приложение
OpenMP
компилятор
OpenMP библиотека
Треды ОС
Пользователь
Переменные
среды

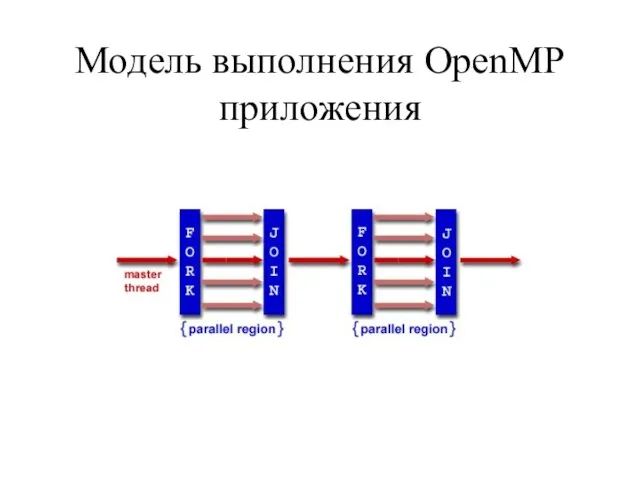
Модель выполнения OpenMP приложения

Работа с вычислительным пространством – число тредов
Мастер-тред имеет номер 0
Число тредов, выполняющих работу определяется:
- переменная окружения OMP_NUM_THREADS
- вызов функции omp_set_num_threads() (может вызываться перед параллельным участком, но не внутри этого участка)
Определение числа процессоров в системе:
omp_get_num_procs()

Работа с вычислительным пространством – динамическое определение числа тредов
В некоторых случаях целесообразно устанавливать число тредов динамически в зависимости от загрузки имеющихся процессоров.
Включить данную опцию можно с помощью переменной среды
OMP_DYNAMIC [TRUE, FALSE]
или с помощью функции omp_set_dynamic(int flag) (может вызываться перед параллельным участком, но не внутри этого участка)
Если flag != 0 , то механизм включается, в противном случае – выключается.

Определение числа процессоров, тредов и своих координат в системе
int omp_get_num_procs() возвращает количество процессоров в системе;
int omp_get_num_threads() возвращает количество тредов, выполняющих параллельный участок (меняется только на последовательных участках);
int omp_get_thread_num() возвращает номер вызывающего треда.

#include
#include
#include
main(int argc, char* argv[])
{
omp_set_num_threads(atoi(argv[1]));
printf("Total number of processors is %d\n",
omp_get_num_procs());
#pragma omp parallel
printf("Hello, World from thread %d of %d\n", omp_get_thread_num(), omp_get_num_threads());
}

Общий синтаксис директив OpenMP
#pragma omp directive_name [clause[clause ...]] newline
Действия, соответствующие директиве применяются
непосредственно к структурному блоку, расположенному за
директивой. Структурным блоком может быть любой оператор,
имеющий единственный вход и единственный выход.
Если директива расположена на файловом уровне видимости, то
она применяется ко всему файлу.

Директива parallel
Данная директива – единственный способ инициировать
параллельное выполнение программы.
#pragma omp parallel [clause ...]
clause: if (scalar_expression)
private (list)
shared (list)
default (shared | none)
firstprivate (list)
reduction (operator: list)
copyin (list)

#include
main () {
int nthreads, tid;
#pragma omp parallel private(nthreads, tid)
{
tid = omp_get_thread_num();
printf("Hello World from thread = %d\n", tid);
if (tid == 0)
{
nthreads = omp_get_num_threads();
printf("Number of threads = %d\n", nthreads);
}
}
}

Опции для данных
Данные, видимые в области, объемлющей блок параллельного
исполнения, являются общими (shared). Переменные,
объявленные внутри блока п.и. считаются распределенными
(private).
Опция private задает список распределенных переменных.
Только shared-переменные в объемлющей параллельном блоке могут быть аргументами опции private
Опция private

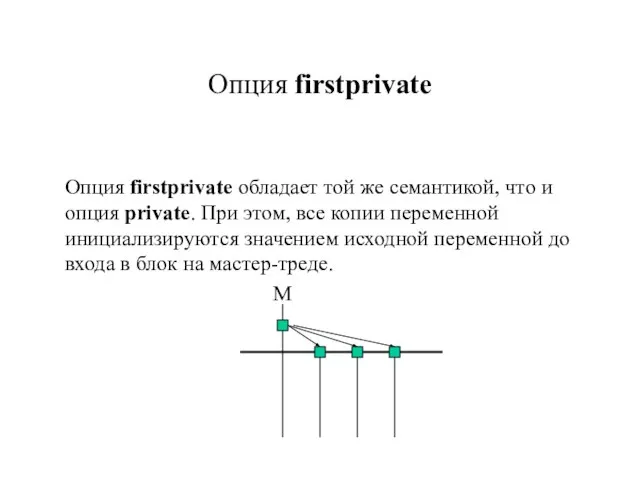
Опция firstprivate обладает той же семантикой, что и
опция private. При этом, все копии переменной инициализируются значением исходной переменной до входа в блок на мастер-треде.
Опция firstprivate
М

Опция default
Опция default задает опцию по-умолчанию для
переменных. Пример:
#pragma omp parallel default(private)
Опция shared
Опция shared задает список общих переменных.
#pragma omp parallel default(private) shared(x)

опция reduction
Опция reduction определяет что на выходе из параллельного блока переменная получит комбинированное значение. Пример:
#pragma omp for reduction(+ : x)
Допустимы следующие операции: +, *, -, &, |, ^, &&, ||

Глобальные общие данные
Проблема: опция private «работает» только для статически-видимых ссылок в пределах параллельного участка:
static int a;
f() {
printf(“%d\n”, a);
}
main() {
#omp parallel private (a)
{
a = omp_num_thread();
f();
}
}
значение a неопределено

Директива threadprivate
#omp threadprivate (список глобальных переменных)
переменные становятся общими для всех тредов:
static int a;
f() {
printf(“%d\n”, a);
}
main() {
#omp threadprivate(a)
#omp parallel {
a = omp_num_thread();
f();
}
}

Опция copyin
Опция copyin директивы parallel определяет порядок инициализации threadprivate-переменных: эти переменные инициализируются значением на master-треде в начале параллельного участка.

Управление распределением
вычислений
Для распределения вычислений применяются
конструкции:
for
sections
single

Директива for
#pragma omp for [clause ...]
clause:
schedule (type [,chunk])
ordered
private (list)
firstprivate (list)
lastprivate (list)
reduction (operator: list)
nowait

Директива предшествует циклу for канонического типа:
for(init-expr, var logical_op b, incr_expr)
init_expr ::= var = expr
logical_op >, <, >=, <=

incr_expr ::= var ++
++ var
var --
-- var
var += incr
var -= incr
var = incr + var
var = var + incr
var = var – incr
var переменная целого типа
incr, lb, b инварианты цикла целого типа

Опция shedule директивы for
Опция shedule допускает следующие аргументы:
static - распределение осуществляется статически;
dynamic - распределение осуществляется динамически (тред,
закончивший выполнение, получает новую порцию итераций);
guided - аналогично dynamic, но на каждой следующей итерации
размер распределяемого блока итераций равен примерно общему
числу оставшихся итераций, деленному на число исполняемых
тредов, если это число больше заданного значения chunk, или
значению chunk в противном случае (крупнее порция –
меньше синхронизаций)
runtime - распределение осуществляется во время выполнения
системой поддержки времени выполнения (параметр chunk не
задается) на основе переменных среды

Особенности опции schedule директивы for
аргумент chunk можноиспользовать только вместе с типами static, dynamic, guided
по умолчанию chunk считается равным 1
распараллеливание с помощью опции runtime осуществляется используя значение переменной OMP_SCHEDULE
Пример. setenv OMP_SCHEDULE “guided,4”

#include
#include
#include
main(int argc, char* argv[])
{
int n, iters, t, i, j;
double *a, *b, *c, alpha = 0.1;
n = atoi(argv[1]);
iters = atoi(argv[2]);
a = (double*)malloc(n * sizeof(double));
b = (double*)malloc(n * sizeof(double));
t = time(NULL);
for(i = 0; i < iters; i ++) {
for(j = 0; j < n; j ++) {
a[j] = a[j] + alpha * b[j];
}
}
t = time(NULL) - t;
printf("sequential loop: %d seconds\n", t);
}
Сложение (с умножением) векторов – последовательный вариант.

#include
#include
#include
#include
main(int argc, char* argv[])
{
int n, iters, t, i, j;
double *a, *b, alpha = 0.1;
n = atoi(argv[1]);
iters = atoi(argv[2]);
a = (double*)malloc(n * sizeof(double));
b = (double*)malloc(n * sizeof(double));
t = time(NULL);
for(i = 0; i < iters; i ++) {
#pragma omp parallel for private(j), firstprivate(n)
for(j = 0; j < n; j ++) {
a[j] = a[j] + alpha * b[j];
}
}
t = time(NULL) - t;
printf("parallel loop: %d seconds\n", t);
}
Сложение (с умножением) векторов – параллельный вариант.

Результаты эксперимента
Компьютер: 2 x 64-разрядный процессор Intel® Itanium-2® 1.6 ГГц.

Директива sections
#pragma omp sections [clause ...]
structured_block
clause: private (list)
firstprivate (list) lastprivate (list)
reduction (operator: list)
nowait
{
#pragma omp section
structured_block
#pragma omp section
structured_block
}

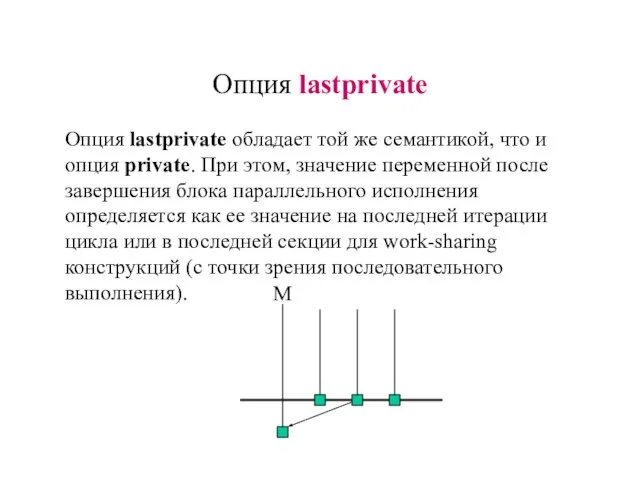
Опция lastprivate обладает той же семантикой, что и
опция private. При этом, значение переменной после завершения блока параллельного исполнения определяется как ее значение на последней итерации цикла или в последней секции для work-sharing конструкций (с точки зрения последовательного выполнения).
Опция lastprivate
М

Директива single
#pragma omp single [clause ...]
structured_block
Директива single определяет что последующий
блок будет выполняться только одним тредом

Директивы синхронизации
master
critical
barrier
atomic
flush
ordered

#pragma omp master
определяет секцию кода, выполняемого только master-тредом
#pragma omp critical [(name)]
определяет секцию кода, выполняемого только одним тредом в данный момент времени
#pragma omp barrier
определяет секцию кода, выполняемого только одним тредом в данный момент времени

#pragma omp atomic
::==
x binop = expr
x ++
++ x
x --
-- x

#paragma omp flush [var-list]
::==
x binop = expr
x ++
++ x
x --
-- x
Следующие содержат неявный flush: barrier, вход и выход из critical, ordered, выход из parallel, for, sections, single

Решение уравнения Пуассона
методом верхней релаксации
d2u/dx2 + d2u/dy2 – a * u = f
1
1
-1
-1
(1-x2)(1-y2)

Разностная схема
uijnew = uij – w /b *((ui-1,j + ui+1,j)/dx2 + (ui,j-1 + +ui,j+1)/dy2 + b * ui,j – fi,j)
b = - (2/dx2 + 2/dy2 + a)