Слайд 2ВОЗВЕДИТЕ В СТЕПЕНЬ ОДНОЧЛЕН
(0,2а3b4)4
1) 0,16а7b8 ;
2) 0,0016а12b116;
3)

0,8а12b16;
4) 0,016а12b16;
Слайд 3ПОВТОРИ ПРАВИЛА
При возведении произведения в степень каждый множитель возводят в эту

степень.
(3а)4=34·а4=81а4
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(а4)3=а4·3=а12
(2а3b5)4=24·а3·4 ·b5·4=16а12b20
Слайд 4НЕПРАВИЛЬНО
Тебе надо повторить правила!

Слайд 6ВЫПОЛНИТЕ УМНОЖЕНИЕ
2с2т ·(-0,5т2с)·(-с2т 4)
1) 10т7с5 ;
2) -10т7с5;
3) т7с5 ;

4) -с5т7.
Слайд 7ПОВТОРИ ПРАВИЛА
При умножении степеней с одинаковыми основаниями основание оставляют без изменений,

а показатели степеней складывают.
а3·а5=а3+5=а8
Произведении двух отрицательных чисел есть число положительное.
-1,5·3=- 4,5
Слайд 8НЕПРАВИЛЬНО
Тебе надо повторить правила!

Слайд 10ВМЕСТО ЗНАКА * ПОСТАВЬТЕ ТАКОЙ ОДНОЧЛЕН, ЧТОБЫ ПОЛУЧИЛОСЬ ВЕРНОЕ РАВЕНСТВО
30 Х5У6Z7:

*= 5Х3У2Z6
6ХУ3ZZ;
2) 6Х2У4ZZ;
3) 6ХУ 3) 6ХУZ 3) 6ХУZ; 3) 6ХУZ;
4) 6 4) 6Х2У3ZZ
Слайд 11ПОВТОРИ ПРАВИЛА
При делении степеней с одинаковыми основаниями основание оставляют прежним, а из

показателя делимого вычитают показатель делителя.
а12: а7=а12-7=а5
Слайд 12НЕПРАВИЛЬНО
Тебе надо повторить правила!

Слайд 14УПРОСТИТЕ ВЫРАЖЕНИЕ
(5а2b2)3 : (5аb)2
1) 5а4b4;
2) 25а4b4;
3) 5а3bb;
4)

5а 4) 5аb 4) 5аb.
Слайд 15ПОВТОРИ ПРАВИЛА
Прежде чем выполнить деление, надо возвести в степень каждый множитель,

а затем выполнить деление степеней с одинаковыми основаниями, при этом основания оставляют без изменений, а из показателя делимого вычитают показатель делителя.
Пример.
(2х2у4)3 : (4ху5)2=8х6у12:16х2у10=0,5х4у2.
Слайд 16НЕПРАВИЛЬНО
Тебе надо повторить правила!

Слайд 18УПРОСТИТЕ ВЫРАЖЕНИЕ
(2т2х2)4 : (4тх)2
1) 2т6х6;
2) т6х6 ;
3) 8т4х4;

4) 2т4х4 .
Слайд 19ПОВТОРИ ПРАВИЛА
Сначала возведи в степень каждый одночлен, а затем выполни деление

одночлена на одночлен, при этом основание не меняется, а из показателя делимого вычитают показатель делителя.
Пример
(2х2у4)3 : (4ху5)2=8х6у12:16х2у10=0,5х4у2.
Слайд 20НЕПРАВИЛЬНО
Тебе надо повторить правила!

Слайд 22УПРОСТИТЕ ВЫРАЖЕНИЕ
55р3q4 : (5рq)0
1) 111) 11р2q3;
2) 11р3q4;
3) 55р3q4;

4) 55р2q3.
Слайд 23ПОВТОРИ ПРАВИЛА
Если а≠0, то а0=1.
Например, 2,30=1; (-8)0 =1; (3ху)0=1.

Слайд 24НЕПРАВИЛЬНО
Тебе надо повторить правила!

Слайд 26Какой из указанных ниже одночленов А удовлетворяет равенству
49а4в6=А2
1) А=-7а2в4;
2) А=

-7а2в3;
3) А=7а2в4;
4) А=24,5а2в3.
Слайд 27ПОВТОРИ ПРАВИЛА
При возведении степени в степень показатели перемножаются, а основание остаётся

неизменным
Пример
(а3в4)5=а15в20.
Слайд 28НЕПРАВИЛЬНО
Тебе надо повторить правила!




























 Компьютер в моей жизни Дмитрий Сушко
Компьютер в моей жизни Дмитрий Сушко Административная компетенция и административные полномочия органов исполнительной власти
Административная компетенция и административные полномочия органов исполнительной власти К пастырям ночью голос прозвучал: Встаньте, не бойтесь, Бог нам радость дал! Все оставить не страшитесь, В град Давидов поспешите, Т
К пастырям ночью голос прозвучал: Встаньте, не бойтесь, Бог нам радость дал! Все оставить не страшитесь, В град Давидов поспешите, Т Особенности обучения иностранному языку студентов физического профиля
Особенности обучения иностранному языку студентов физического профиля Позиционирование информационного сервиса Д.В. Ландэ, к. т. н., заместитель директора Информационного центра "ЭЛВИСТИ"
Позиционирование информационного сервиса Д.В. Ландэ, к. т. н., заместитель директора Информационного центра "ЭЛВИСТИ" Конституция Российской Федерации Гражданский кодекс Российской Федерации Таможенный кодекс Российской Федерации
Конституция Российской Федерации Гражданский кодекс Российской Федерации Таможенный кодекс Российской Федерации ЗАО «ММВБ-Северо-Запад»: технический центр- «окно» в ММВБ
ЗАО «ММВБ-Северо-Запад»: технический центр- «окно» в ММВБ Гофман, Эрнест Теодор Амадэй
Гофман, Эрнест Теодор Амадэй Полимеры. Пластмассы. Волокна.
Полимеры. Пластмассы. Волокна. Презентация на тему мое школьное расписание My school timetable
Презентация на тему мое школьное расписание My school timetable Клуб PR-специалистов банковского сектора: выбор пути
Клуб PR-специалистов банковского сектора: выбор пути Изостудия Этюд. Графика (упражнение)
Изостудия Этюд. Графика (упражнение) Виды риэлторских услуг. Система оплаты
Виды риэлторских услуг. Система оплаты Национальная модель аккредитации Казахстана Стандарты и критерии институциональной аккредитации Директор НАЦ МОН РК, профессор
Национальная модель аккредитации Казахстана Стандарты и критерии институциональной аккредитации Директор НАЦ МОН РК, профессор Размножение на клеточном уровне
Размножение на клеточном уровне Идеи управления Р.Оуэна
Идеи управления Р.Оуэна  Проблемы банковского обеспечения военной организации государства
Проблемы банковского обеспечения военной организации государства Средства индивидуальной защиты органов дыхания и кожи
Средства индивидуальной защиты органов дыхания и кожи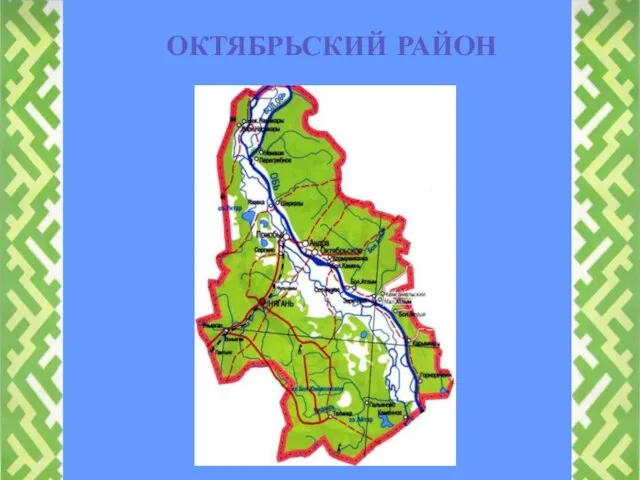 Октябрьский район
Октябрьский район Профессии
Профессии Древние гунны
Древние гунны Использование технологий Citrix при консолидации ИТ
Использование технологий Citrix при консолидации ИТ Эскиз музейных ветрин
Эскиз музейных ветрин Ювелирное искусство Древнего Египта
Ювелирное искусство Древнего Египта Витамины в нашей жизни
Витамины в нашей жизни Значение гуманитарных проектов для обучения, развития и воспитания школьников
Значение гуманитарных проектов для обучения, развития и воспитания школьников Care campaign 2016. In-store support. Кампания: об’єднуйте сім’ю турботою
Care campaign 2016. In-store support. Кампания: об’єднуйте сім’ю турботою Внешняя политика
Внешняя политика