ОПТИМАЛЬНОЕ ПРЯМОЕ ОРЕБРЕНИЕ РАДИАТОРАВилипп К.А.ОАО «НПЦ «Полюс»634050, г. Томск, пр. Кирова, 56«в»

В современных электронных приборах и электрических машинах, космических
аппаратах, ядерных реакторах и в других технических устройствах для увеличения
теплопередачи и уменьшения габаритов теплообменной аппаратуры широко используются оребренные (развитые) поверхности.

Определить оптимальные параметры ребристой системы теплоотвода, для обеспечения передачи заданных тепловых потоков при минимальной массе и объеме системы.
Цель работы

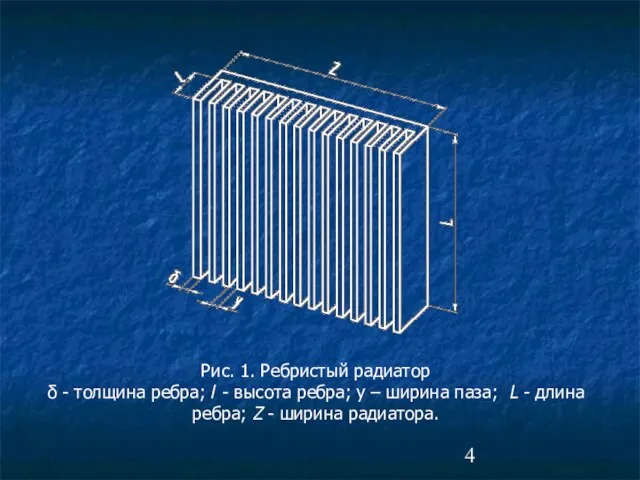
Рис. 1. Ребристый радиатор
δ - толщина ребра; l - высота ребра; y – ширина паза; L - длина ребра; Z - ширина радиатора.

Коэффициент эффективности прямого прямоугольного ребра:
где: - толщина ребра
- высота ребра
- коэффициент теплоотдачи
- коэффициент теплопроводности
- коэффициент из таблицы гиперболических функций.

Выполнен расчет при различных значениях толщины и высоты ребра, для радиатора из алюминиевого сплава АМг6. Данные представлены графиком.

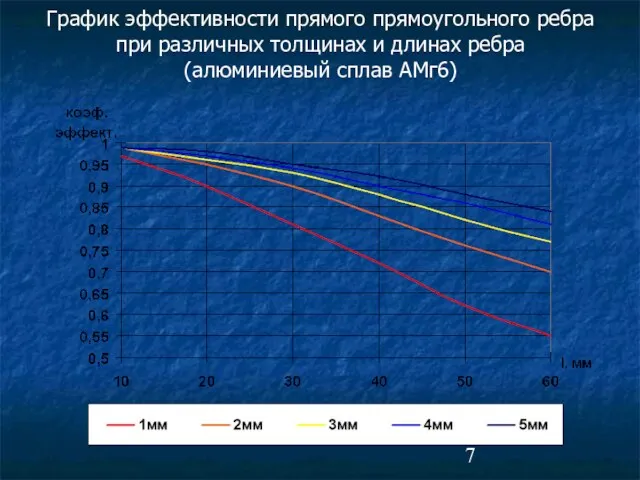
График эффективности прямого прямоугольного ребра при различных толщинах и длинах ребра
(алюминиевый сплав АМг6)

Из графика видно, что с увеличением высоты ребра, значительно возрастает температурный градиент (перепад температуры) и падает коэффициент эффективности.

Формулы расчета отводимой мощности радиатора
коэффициент теплоотдачи воздуха
число Нуссельта
число Рейнольдса
тепловой поток отводимый ребром

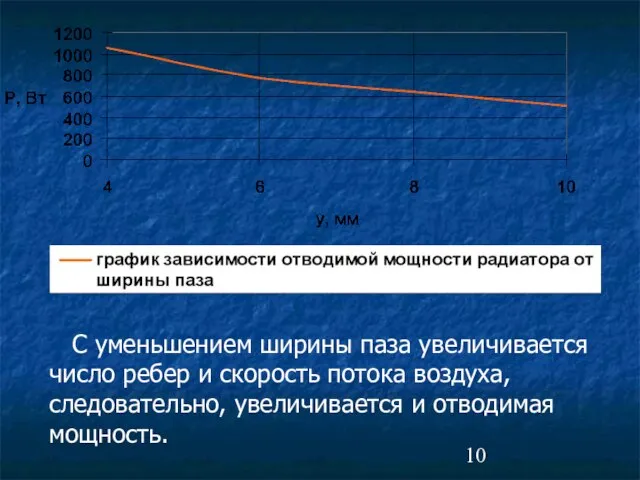
С уменьшением ширины паза увеличивается число ребер и скорость потока воздуха, следовательно, увеличивается и отводимая мощность.

Экспериментальные данные
Подводимая мощность 690 Вт; плоскость S = Z·L = 20,4·30 = 612см² ; количество ребер N = 20; ширина паза y=6мм; толщина ребра б = 4мм; высота ребра l = 19 мм;
температура в помещении 31 ºС;
температура основания 74 ºС;
температура на конце ребра 53 ºС;
температура выдуваемого воздуха 46 ºС;
перегрев между охлаждаемым прибором и воздухом 43 °С.
расчетная отводимая мощность для данного радиатора 590 Вт, погрешность расчета 14,5 %

Заключение
Произведен анализ оптимальных значений радиатора с прямыми прямоугольными ребрами.
Найдена оптимальная толщина и высота ребра для радиатора выполненного из алюминиевого слава АМг6.
Представленные экспериментальные данные подтверждают данную методику расчета.