ОПТИМИЗАЦИЯ ПЕРЕЛЕТОВ С МАЛОЙ ТЯГОЙ В ЗАДАЧЕ ТРЕХ ТЕЛ

Метод транспортирующей траектории (МТТ)
Метод приближенной оптимизации перелетов с идеально регулируемой малой тягой между двумя заданными положениями, основанный на линеаризации траектории перелета около некоторой опорной кеплеровской орбиты (транспортирующей траектории).
В.В. Белецкий, В.А. Егоров, Межпланетные полеты с двигателями постоянной мощности, Космические исследования, 1964, № 3
Орбитальная система координат
Постоянная мощность тяги
Решение частично в квадратурах
Приемлемая точность только при небольшой угловой дальности

Модифицированный МТТ
Инерциальная система координат
Полностью аналитическое решение для постоянной мощности
Решение в квадратурах для произвольного закона изменения мощности
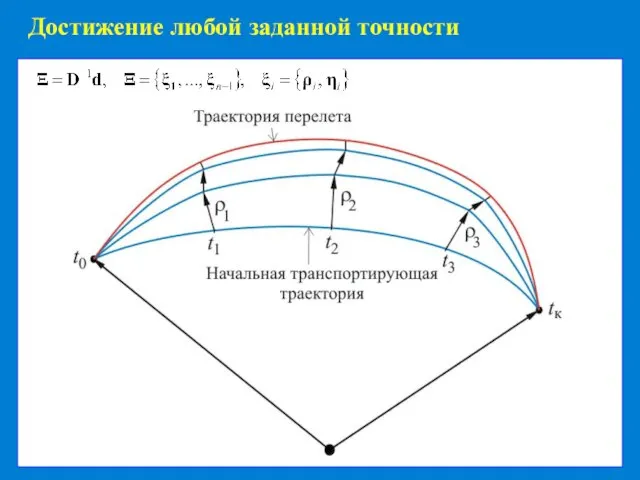
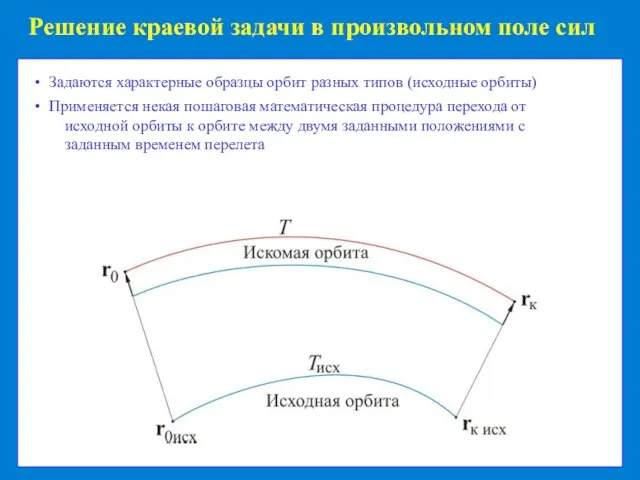
Ненулевые концевые смещения транспортирующей
траектории, повышающие точность аппроксимации
Возможность частично заданных граничных условий
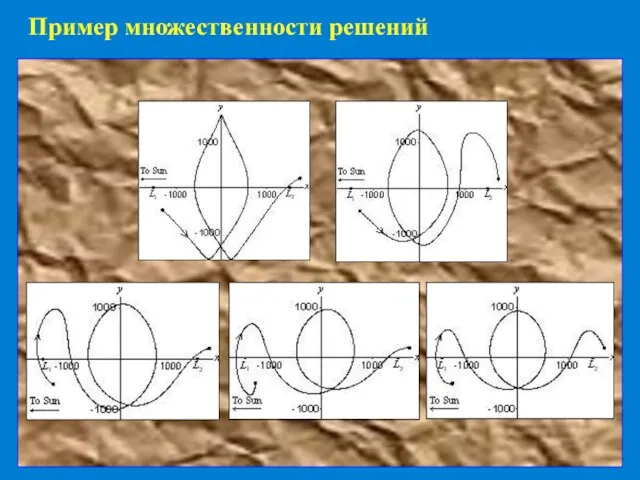
Перелеты с большой угловой дальностью (включая многовитковые орбиты)
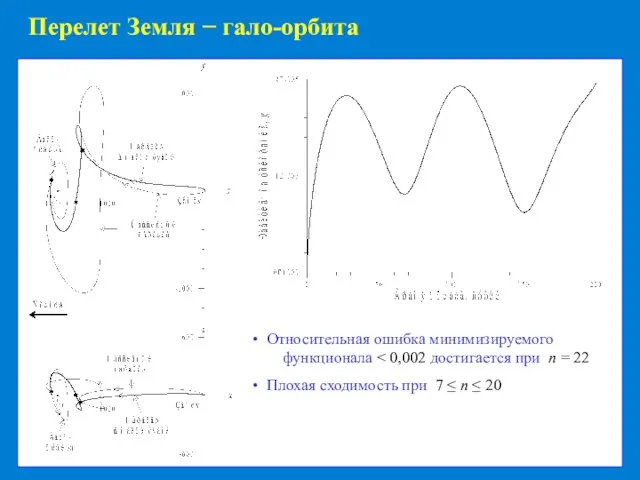
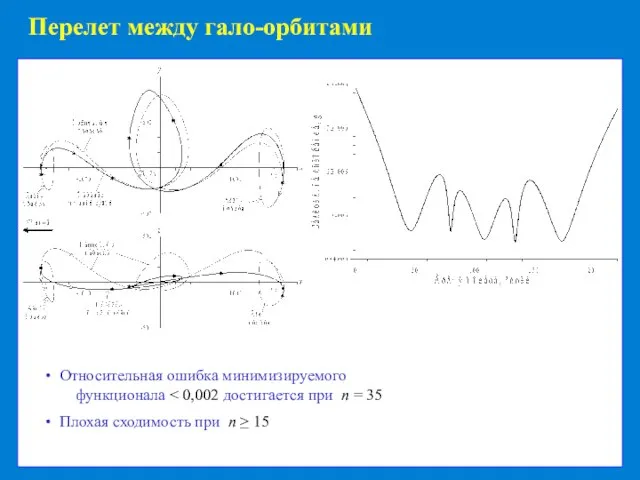
Возможность получения любой требуемой точности вычислений
Возможность облета нескольких небесных тел
Применение при линейных ограничениях на направление тяги
А.А. Суханов, Оптимизация перелетов с малой тягой, Космические исследования, 1999, № 2
А.А. Суханов, Оптимизация межпланетных перелетов с малой тягой, Космические исследования, 2000, № 6
А.А. Суханов, А.Ф.Б. де А. Прадо, Модификация метода транспортирующей траектории, Космические исследования, 2004, № 1
А.А. Суханов, А.Ф.Б. де А. Прадо, Оптимизация перелетов при ограничениях на направление тяги, Космические исследования (в печати)

МТТ в произвольном поле сил
α – вектор реактивного ускорения КА (тяга)
– уравнение движения, g = {0, α}
x(t0) = x0 , x(tк) = xк – граничные условия
y = y(t) – решение уравнения
y(t0) = y0 , y(tк) = yк − граничные условия на транспортирующей траектории

МТТ в произвольном поле сил
Свойства:
Матрица S = S(t, t + Δt) является невырожденной положительно определенной для любых значений t и Δt > 0
Оптимальная тяга может обращаться в нуль лишь в изолированных точках, причем в этих точках знак тяги меняется на противоположный (т.е. эти точки являются точками переключения) и число таких точек конечно

Обеспечение любой заданной точности
Интервал времени полета разбивается на n подынтервалов и МТТ применяется к каждому подынтервалу в отдельности.
Проблема заключается в нахождении граничных условий ξ1, ..., ξn−1 для подынтервалов.
− вектор размерности 6n − 6
− симметричная матрица порядка 6n − 6
Di, Ei − матрицы 6-го порядка, вычисляемые на i-м подынтервале

Достижение любой заданной точности

Ограничения на направление тяги
− проективная матрица
Bα = 0 B = B(x, t) − матрица ранга 1 или 2

Способы вычисления необходимых компонентов
Произвольное поле сил
Матрицы Φ, Ψ вычисляются численным интегрированием уравнений в вариациях совместно с уравнениями движения
Матрица S вычисляется в квадратурах
Транспортирующая траектория является решением краевой задачи
Задача двух тел
Матрицы Φ, Ψ вычисляются аналитически
Матрица S вычисляется аналитически или в квадратурах
Транспортирующая траектория: кеплеровская орбита, найденная путем решения задачи Ламберта
Основным препятствием на пути применения МТТ в произвольном поле сил является проблема нахождения транспортирующей траектории заданного типа

Пример множественности решений

Решение краевой задачи в произвольном поле сил
Задаются характерные образцы орбит разных типов (исходные орбиты)
Применяется некая пошаговая математическая процедура перехода от исходной орбиты к орбите между двумя заданными положениями с заданным временем перелета

Модель движения Хилла
Уравнения движения:
Коллинеарные точки либрации L1 и L2:
Матрица изохронных производных Ф:

Исходные орбиты в модели движения Хилла

Демонстрация метода

Перелет Земля − гало-орбита
Относительная ошибка минимизируемого функционала < 0,002 достигается при n = 22
Плохая сходимость при 7 ≤ n ≤ 20

Перелет между гало-орбитами
Относительная ошибка минимизируемого функционала < 0,002 достигается при n = 35
Плохая сходимость при n ≥ 15